3957
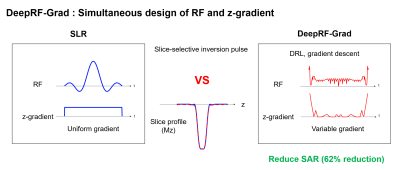
DeepRF-Grad: Simultaneous design of RF pulse and slice selective gradient using self-learning machine1Department of Electrical and Computer Engineering, Seoul National University, Seoul, Korea, Republic of
Synopsis
A deep reinforcement learning method referred to as DeepRF-Grad, is newly developed to design an RF pulse and a slice selective gradient waveform. The method is demonstrated for slice-selective inversion and compared with SLR and VERSE-designed pulses. The DeepRF-Grad designed pulse showed lower SAR (SLR: 13.2mG2s, VERSE: 6.37mG2s, DeepRF-Grad: 5.00mG2s). When designed for off-resonance robustness, the DeepRF-Grad generated enhanced off-resonance characteristics compared to that of VERSE-designed pulse, while showing similar SAR.
Introduction
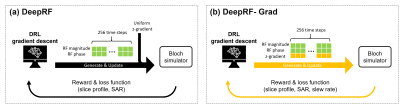
In MR imaging, a high specific absorption rate (SAR) of a radiofrequency (RF) pulse is a significant problem in clinical use, particularly for high field systems. To reduce SAR, a variable-rate selective excitation (VERSE) method, which remaps uniform slice-selective gradient into the time-varying gradient, was introduced1. As reported, however, VERSE pulses are vulnerable to off-resonance frequency, limiting the applicability of the method. Recently, deep reinforcement learning (DRL)-powered RF pulse design has been proposed, demonstrating improved performance in SAR2,3. In this work, we extended the dimension of the design space in DeepRF3 to include both RF pulse and slice-selective gradient waveform (Gz). This new method is named DeepRF-Grad (Fig 1) and is tested to generate i) SAR-reduced design and ii) SAR-reduced and off-resonance robust design, while satisfying hardware constraints (i.e., gradient slew rate and max gradient limits).Methods
For a conventional RF pulse, a slice-selective linear-phase inversion pulse is designed using Shinnar-Le-Roux (SLR)4,5. The parameters are as follows: pulse duration = 3.873 ms, time-bandwidth product = 2.711, stopband ripple = 1%, and passband ripple = 1%. This pulse is redesigned using the VERSE algorithm to reduce SAR6.In DeepRF-Grad, the pulse duration is the same and the ripple conditions are designed to match the conventional RF pulse. The design process of DeepRF-Grad is as follows: first, magnitude and phase parts of the RF pulse and slice selective gradient waveform (Gz) are simultaneously designed using DRL (3x256 points). Secondly, these designs are jointly updated using gradient descent until they converged to an optimal point (Fig 2).
To design a slice-selective inversion pulse while regularizing SAR, the reward of DRL is devised as follows:
$$reward=-\frac{1}{N}\sum_{z_p\in{Z_{pass}}}M_z(RF,G_z,z_p)+\frac{1}{M}\sum_{z_s\in{Z_{stop}}}M_z(RF,G_z,z_s)-c_{SAR}SAR$$
where N (= 24) is the number of z-positions in the passband (Zpass), and M (= 86) is the number of z-positions in the stopband (Zstop), Mz is the longitudinal magnetization, and cSAR (= 0.3) is a coefficient for the SAR regularizer term. Each training of the DRL agent consists of 1000 epochs. After training, RF pulses and Gz generated with the top 1000 highest rewards are selected as seeds for the second part of DeepRF-Grad, gradient descent.
The objective of the gradient descent step is to match the slice profile to that of the SLR-designed result while minimizing SAR and keeping the slew rate under the limit. Two types of designs are developed: i) SAR minimized design with off-resonance sensitivity comparable to that of VERSE, and ii) off-resonance robust design with reduced SAR. The loss function, which is minimized via gradient descent, is designed as follows:
$$loss=\sum_{w_o\in{W}}\parallel{M_z(RF,G)-M_z(SLR)}\parallel+c_1SAR+c_2\sum_{i=1}^{256}u(slew_i-slew_{max})$$
where wo means off-resonance frequencies, c1 and c2 are coefficients, u is a unit step function, slewi is a gradient slew rate for each time step, slewmax is the slew rate limit (= 170 mT/(m*ms)). The off-resonance frequencies are included only for the off-resonance robust design. The derivatives of the loss function with respect to each of the RF pulse and Gz are computed via automatic differentiation. The gradient descent is repeated until the RF pulse and Gz converge.
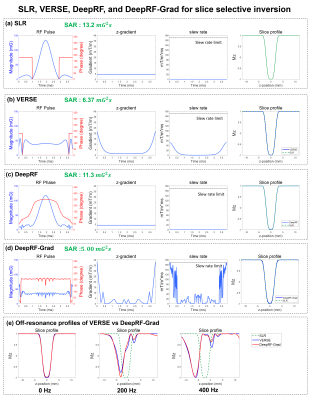
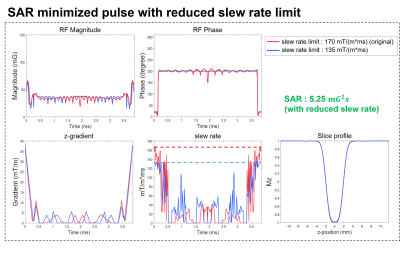
The SLR, VERSE, DeepRF, and DeepRF-Grad designs are evaluated in terms of their slice profile and SAR. Additionally, the slice profiles of the VERSE and DeepRF-Grad designs are compared at two additional off-resonance frequencies (200 Hz, and 400 Hz). For a fair comparison, a VERSE designed pulse that has a similar SAR to the DeepRF-Grad pulse is produced. Lastly, an additional DeepRF-Grad design is produced for a low slew rate condition (135 mT/(m*ms); 20% lower slew rate), comparing for the SAR and slice profile.
Results
[SAR minimized design]The SARs of the four designs are 13.2mG2s for SLR, 6.37 mG2s for VERSE, 11.3mG2s for DeepRF, and 5.00 mG2s for DeepRF-Grad, demonstrating a reduction of 62% in SAR when comparing the DeepRF-Grad result with that of SLR (Fig. 3). The slice profiles (last column in Fig. 3) reveal comparable results in all designs. In DeepRF-Grad, the mean Mz in the passband is -0.97 (SLR: -0.99), and the stopband ripple is 1.19% (SLR: 0.21%). No hardware constraint is violated. When the off-resonance profiles are compared, both VERSE and DeepRF-Grad results show similar profiles (Fig. 3e).
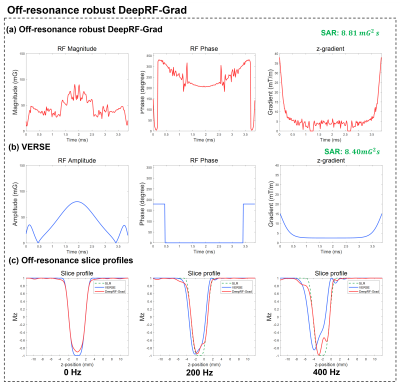
[Off-resonance robust design]
The SARs are 8.81mG2s for DeepRF-Grad, and 8.40 mG2s for VERSE. Figure 4 illustrates the VERSE and off-resonance robust DeepRF-Grad designs with similar SAR. DeepRF-Grad reveals an improved off-resonance profile, particularly at a high off-resonance frequency (400Hz).
Conclusion and Discussion
In this study, we propose a deep learning method that simultaneously designs RF pulse and slice-selective gradient waveform. The results show that DeepRF-Grad can reduce SAR by 62% when compared to the SLR pulse. Additionally, DeepRF-Grad can be utilized to design an off-resonance robust RF/Gz design that has 35% lower SAR than the SLR pulse. Since DeepRF-Grad designed gradient shows a high slew rate at the edges, an eddy-current-induced artifact could exist. This may be mitigated by setting a lower limit to the slew rate, which resulted in a similar pulse while maintaining SAR reduction performance (60% reduction) (Fig. 5).Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF- 2018R1A2B3008445), and Brain Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2019M3C7A1031994).References
1. Steven Conolly, Dwight Nishimura, Albert Macovski, Gary Glover, Variable-rate selective excitation, Journal of Magnetic Resonance (1969), Volume 78, Issue 3, 1988, Pages 440-458, ISSN 0022-2364.
2. Dongmyung Shin, Sooyeon Ji, Doohee Lee, et al. Deep Reinforcement Learning Designed Shinnar-Le Roux RF Pulse using Root-Flipping: DeepRFSLR. IEEE Transactions on Medical Imaging 2020 39(12): 4391-4400.
3. Dongmyung Shin and Jongho Lee. DeepRF: Designing an RF pulse using a self-learning machine. Highlight session of 28th ISMRM Virtual Conference & Exhibition, 08-14 August 2020.
4. J. Pauly, P. Le Roux, D. Nishimura, and A. Macovski, "Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm (NMR imaging)," in IEEE Transactions on Medical Imaging, vol. 10, no. 1, pp. 53-65, March 1991.
5. Gerald B. Matson, An integrated program for amplitude-modulated RF pulse generation and re-mapping with shaped gradients, Magnetic Resonance Imaging, Volume 12, Issue 8, 1994, Pages 1205-1225.
6. Neville D. Gai, Yuval Zur, Design and optimization for variable-rate selective excitation using an analytic RF scaling function, Journal of Magnetic Resonance, Volume 189, Issue 1, 2007, Pages 78-89.
Figures