3954

Multidimensional RF Pulse Design with Known Spatial Encoding Imperfections

Ziwei Zhao¹, Nam G. Lee², and Krishna S. Nayak^1,2
¹Ming Hsieh Department of Electrical and Computer Engineering, Viterbi School of Engineering, University of Southern California, Los Angeles, CA, United States, ²Department of Biomedical Engineering, Viterbi School of Engineering, University of Southern California, Los Angeles, CA, United States

Synopsis

We describe a multidimensional small-tip RF pulse design procedure that incorporates concomitant field effects and gradient imperfections. Nonrotating concomitant fields in the reference frame are modeled as a Bloch-Siegert shift in the rotating frame and treated as higher-order phase terms in the excitation k-space formalism. We evaluate the effects of concomitant fields using simulations that mimic current 0.55T, 1.5T, 3T, and 7T systems. The proposed procedure produces more accurate excitation patterns, especially when concomitant field effects are strongest, i.e., low field strengths, off-isocenter, and longer pulse durations.

INTRODUCTION

Multidimensional RF pulses have many common uses including localization,¹ motion tracking,² and inner volume imaging.³ Excitation performance can be compromised by gradient imperfections, and solutions already exist.⁴ The effects of concomitant fields (generated whenever linear gradients are active⁵) have thus far not been considered during RF pulse design.

Here, we describe a new small-tip excitation k-space formalism that incorporates concomitant field effects. The non-rotating concomitant field in the reference frame is approximated as a Bloch-Siegert shift ^6,7 in the rotating frame, and is modeled as spatiotemporal higher-order phase. These are identical to the analytic expressions derived for MR acquisition in the presence of concomitant fields,⁵ demonstrating yet another symmetry between excitation k-space and acquisition k-space.⁸

THEORY

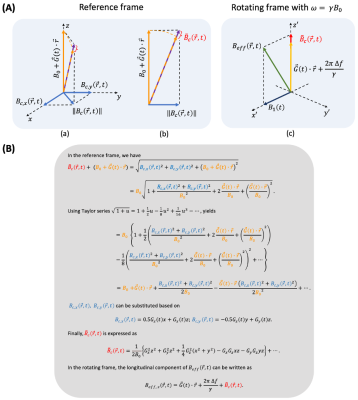
Embedding concomitant field terms into reVERSE design. Based on Grissom et al.,⁹ the spatial and time varying concomitant field $$$B_{c}(\vec{r},t)$$$ can be included as:$$M_{xy}(\vec{r},T)=j\gamma M_0\sum_{\nu=0}^{N_{\nu}-1}s_{\nu}(\vec{r})\int_{0}^{T}\left(B_{1,\nu}(t)+B_c(\vec{r},t)e^{-j \omega_0t}\right)e^{j\Delta f(\vec{r})(t-T)}e^{j\vec{k}(t)\cdot\vec{r}}dt \tag{1}$$where $$$M_{xy}(\vec{r},T)$$$is the transverse magnetization at time $$$T$$$, $$$\vec{r}$$$ is spatial position, $$$\gamma$$$ is the gyromagnetic ratio, $$$M_0$$$ is the equilibrium magnetization, $$$N_{\nu}$$$ is the number of transmit coils, $$$s_{\nu}(\vec{r})$$$ and $$$B_{1,\nu}(t)$$$ are the dimensionless spatial transmit sensitivity and RF pulse waveform for coil $$$\nu$$$, respectively. $$$B_c(\vec{r},t)e^{-j\omega_0 t}$$$ represents the transformed concomitant field in the rotating frame (counter-clockwise) with on resonance frequency $$$\omega_0=\gamma B_0$$$. $$$\Delta f(\vec{r})$$$ denotes static off-resonance. $$$\vec{k}(t)=-\gamma\int_{t}^{T}\vec{G}(s)ds$$$ refers the excitation k-space trajectory with a time varying gradient $$$\vec{G}(s)$$$.

Based on Bernstein et al.,⁵ the induced concomitant field can be described as$$B_c(\vec{r},t)=(-0.5G_z(t)x+G_x(t)z) + j(-0.5G_z(t)y+G_y(t)z), \tag{2}$$where $$$G_x(t)$$$, $$$G_y(t)$$$ and $$$G_z(t)$$$ are applied gradient waveforms and $$$x$$$, $$$y$$$ and $$$z$$$ denote physical coordinates. Transforming $$$B_c(\vec{r},t)$$$ to the rotating frame requires fine sampling intervals (nanoseconds), whereas iteratively solving the least square problem is impractical. Therefore, an approximation is needed to make this computationally feasible.

Practical solution: Bloch-Siegert (BS) shift approximation. We approximate the concomitant field $$$B_c(\vec{r},t)$$$ as a BS shift,¹⁰ under the assumption that the magnitude of main field $$$B_0$$$ is substantially greater than the perturbed concomitant field, i.e., $$$|B_0|>\!\!>|B_c(\vec{r},t)|$$$. Details are illustrated in Figure 1. The approximated $$$\tilde{B_c}(\vec{r},t)$$$ includes higher order phase terms, which are identical to the analytic expressions derived for MR acquisition.⁵ Thus, the concomitant field effect can be treated as an additional contribution to the static $$$B_0$$$ that arises from the time-varying off-resonance component during RF excitation.

METHODS

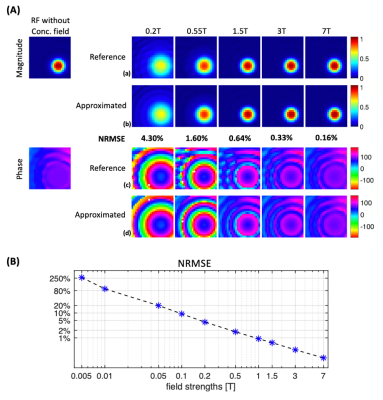
Bloch-Siegert Approximation. We evaluated the estimation accuracy across field strengths (from 0.005T to 7T) using an 8ms 2D excitation RF pulse¹with a single-shot spiral-in k-space trajectory. The dwell time was set to 0.7ns. The profile was set 20cm away from the isocenter along the physical z axis (B₀ direction). Normalized root mean-square excitation error (NRMSE) was calculated for the approximated excitation profiles relatively to the profiles with the concomitant field in the reference frame as Eq. [2].

Multidimensional RF pulse design. The spatially selective multichannel RF pulses were designed using the method by Grissom et al.⁹ The desired excitation profile was a 52×52mm² square beam. The single-shot k-space trajectory supports 128×128mm² FOV with undersampling factor of 2. We utilized published GIRF measurements (Setup A by Çavuşoğlu et al.¹¹), and published B₁⁺ and ΔB₀ maps (3T with an 8-element parallel transmit by Malik et al.¹²).

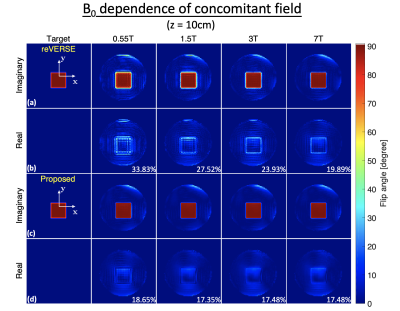
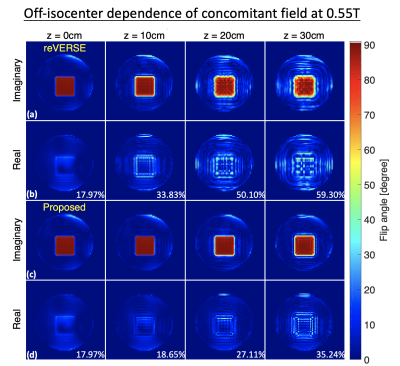
Improved Pulse Design. We compared the proposed procedure with the reVERSE method¹¹with consideration of the concomitant field. The impact and correction of concomitant field was demonstrated through B₀ dependence (0.55T, 1.5T, 3T and 7T), distances from isocenter (0cm-30cm) along z axis, and pulse durations (16, 26, 51ms with 32, 64, 128mm unaliased FOV, respectively). NRMSEs relatively to the desired profile were calculated.

RESULTS and DISCUSSION

Figure 2 shows the concomitant field estimation accuracy using a BS Shift. The estimation error is smaller for larger B₀. The approximation yields NRMSE<5% for B₀≥0.2T.

Figure 3 demonstrates the B₀ dependence of concomitant fields. The effects are large at low field (0.55T) and diminish with field strength (1.5T, 3T and 7T) using the reVERSE method (row a, b). The proposed method (row c, d) reduces NRMSE in every case, but the improvement is greatest at low field. At 0.55T, the proposed method reduced NRMSE to 18.44% from 33.83% (reVERSE).

Figure 4 demonstrates the off-isocenter dependence at 0.55T. Using the reVERSE method (a, b), the concomitant effects increase with displacement (z = 30cm). The proposed method (c, d) mitigates these errors, and provides 50%-60% reduction in NRMSEs.

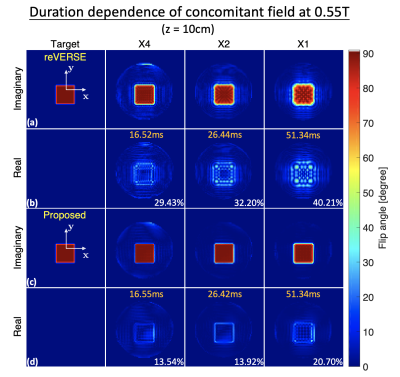
Figure 5 demonstrates the pulse duration dependence. The concomitant field induced errors increase with pulse duration. The proposed method improves NRMSE by more than 50% in all circumstances.

This work has many potential applications ranging from cylindrical excitations used for respiratory navigators to 3D selective excitations for tumor spectroscopy. We took cylindrical 2D excitations as an exemplar because they are widely used in cardiac and thoracic imaging, which appears to be promising at low field strengths^13–15 where concomitant fields are substantial.

CONCLUSION

We demonstrate a new multidimensional small-tip RF pulse design procedure that incorporates concomitant field effects. This new procedure provides more accurate excitations in all scenarios tested. In many cases, excitation profile error was reduced by more than 50%. The impact is greatest in scenarios where concomitant field effects are substantial, such as low field strengths, off-isocenter, and long RF pulse durations.

Acknowledgements

This work was supported by NIH Grants R01-HL130494, R01-DC007142 and NSF Grant #1828763.

References

1. Pauly JM, Nishimura D, Macovski A. A k-Space Analysis of Small-Tip-Angle Excitation. J. Magn. Reson. 1989;213:544–557.

2. Nehrke K, Börnert P, Groen J, Smink J, Böck JC. On the performance and accuracy of 2D navigator pulses. Magn. Reson. Imaging 1999;17:1173–1181.

3. Yip CY, Fessler JA, Noll DC. Iterative RF pulse design for multidimensional, small-tip-angle selective excitation. Magn. Reson. Med. 2005;54:908–917.

4. Wu X, Vaughan JT, Uǧurbil K, Van De Moortele PF. Parallel excitation in the human brain at 9.4 T counteracting k-space errors with RF pulse design. Magn. Reson. Med. 2010;63:524–529.

5. Bernstein MA, Zhou XJ, Polzin JA, et al. Concomitant gradient terms in phase contrast MR: Analysis and correction. Magn. Reson. Med. 1998;39:300–308.

6. Bloch F, Siegert A. Magnetic resonance for nonrotating fields. Phys. Rev. 1940;57:522–527.

7. Ramsey NF. Resonance transitions induced by perturbations at two or more different frequencies. Phys. Rev. 1955;100:1191–1194.

8. Börnert P, Aldefeld B. On spatially selective RF excitation and its analogy with spiral MR image acquisition. Magn. Reson. Mater. Physics, Biol. Med. 1998;7:166–178.

9. Grissom W, Yip CY, Zhang Z, Stenger VA, Fessler JA, Noll DC. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn. Reson. Med. 2006;56:620–629.

10. Sacolick LI, Wiesinger F, Hancu I, Vogel MW. B1 mapping by Bloch-Siegert shift. Magn. Reson. Med. 2010;63:1315–1322.

11. Cavusoglu M, Mooiweer R, Pruessmann KP, Malik SJ. VERSE-guided parallel RF excitations using dynamic field correction. NMR Biomed. 2017;30:1–13.

12. Malik SJ, Hajnal J V. Phase relaxed localized excitation pulses for inner volume fast spin echo imaging. Magn. Reson. Med. 2016;76:848–861.

13. Bandettini WP, Shanbhag SM, Mancini C, et al. A comparison of cine CMR imaging at 0.55 T and 1.5 T. J. Cardiovasc. Magn. Reson. 2020;22:1–10.

14. Restivo MC, Ramasawmy R, Bandettini WP, Herzka DA, Campbell-Washburn AE. Efficient spiral in-out and EPI balanced steady-state free precession cine imaging using a high-performance 0.55T MRI. Magn. Reson. Med. 2020;84:2364–2375.

15. Campbell-Washburn AE, Ramasawmy R, Restivo MC, et al. Opportunities in interventional and diagnostic imaging by using high-performance low-field-strength MRI. Radiology 2019;293:384–393.

Figures

Figure 1. Concomitant field effects approximated as a Bloch-Siegert shift. (A) Reference frame visualization of (a,b) the concomitant $$$B_c(\vec{r},t)$$$, $$$B_0$$$, and gradient field $$$\vec{G}(t)\cdot\vec{r}$$$, and Rotating frame visualization (c) showing that the $$$\tilde{B_c}(\vec{r},t)$$$ approximation can be treated as additional off-resonance in the rotating frame. (B) Detailed derivations.

Figure 2. Concomitant field estimation accuracy. (A) (left) Original 2D RF pulse excitation profile (magnitude: top & phase: bottom). (right) Magnitude (row a, b) and phase (row c, d) of the reference profiles (a, c) and estimated profiles (b, d) using Bloch-Siegert approximation at 0.2T, 0.55T, 1.5T, 3T and 7T. NRMSE results are 4.30%, 1.60%, 0.64%, 0.33% and 0.16% from 0.2T to 7T, respectively. Reference method simulates the concomitant field in the reference frame. (B) NRMSE as a function of field strength. Note that NRMSE is < 5% for B₀ ≥ 0.2 Tesla.

Figure 3. B₀ dependence of concomitant field and the proposed RF pulse design strategy. (a,c) Imaginary and (b,d) real parts of excitation profiles using (a,b) reVERSE and (c,d) proposed method. Shown are the target profile (1^stcolumn) and excitations across field strengths at 0.55T, 1.5T, 3T and 7T (2^nd – 5^th columns). NRMSEs are reported at the bottom right. Notice that NRMSE decreases as B₀ increases, and errors are mitigated using the proposed method.

Figure 4. Off-isocenter dependence of concomitant field effects at 0.55T. (a,c) Imaginary and (b,d) real parts of excitation profiles using (a,b) reVERSE and (c,d) the proposed method. Shown are excitation profiles at difference distances from isocenter: z = 0cm, 10cm, 20cm and 30cm (1^st – 4^th columns). NRMSEs are reported at the bottom right. Notice that NRMSE increases with increased off-isocenter distances. The proposed method completely mitigates NRMSE for shifts up to 10cm, and mitigates NRMSE by ~50% for shifts up to 30cm.

Figure 5. Pulse duration dependence of concomitant field effects at 0.55T. (a,c) Imaginary and (b,d) real parts of excitation profiles using (a,b) reVERSE and (c,d) the proposed method. Shown are ideal profiles (1^st column) and excitation profiles with acceleration factor 4, 2, and 1 (2^nd – 4^th columns), corresponding to a larger unaliased FOV. Pulse durations (orange) and NRMSEs (white) are reported. Notice that NRMSE increases with pulse duration, and these errors are substantially reduced using the proposed method.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

3954