3952

Time optimal control based design of robust inversion pulses

Christina Graf¹, Martin Soellradl¹, Armin Rund², Christoph Stefan Aigner³, and Rudolf Stollberger¹
¹Graz University of Technology, Institute of Medical Engineering, Graz, Austria, ²Institute of Mathematics and Scientific Computing, University of Graz, Graz, Austria, ³Physikalisch-Technische Bundesanstalt (PTB), Braunschweig and Berlin, Berlin, Germany

Synopsis

The aim of this work is to design short and B₀- and B₁-robust inversion pulses by optimal control. A time-optimal control framework is used that incorporates variations within B₀- and B₁-fields. The optimized RF pulse is compared numerically to two hyperbolic-secant pulses and shows a very good efficiency over a broad set of B₀-offsets and B₁-scalings. Two phantom measurements are performed on a 3T MRI system for various scalings of B₁ that verify the results, one with a cylindrical MRI phantom, the other one with oil and water with a contrast agent, demonstrating also the B₀-robustness of the proposed pulse.

Introduction

Composite¹ and adiabatic² pulses fulfill the requirement of $$$B_{1}$$$-robustness, however, at the cost of a higher pulse energy³. Therefore, there is still demand^4,5 for $$$B_{0}$$$- and $$$B_{1}$$$-robust inversion pulses with a high inversion efficiency. Furthermore, variations within the $$$B_{0}$$$-field can affect the flip angle substantially⁶. RF pulse optimization by means of optimal control yields excellent efficiency results while addressing RF energy, hardware constraints and minimizing the pulse duration^7,8. Moreover, optimal control techniques were used for the design of $$$B_{0}$$$- and $$$B_{1}$$$-robust RF pulses^9,10,11. In a preceding work¹², $$$B_{1}$$$-robust, slice-selective inversion pulses with a fixed pulse duration were optimized. Below, the work is extended to time optimal control i.e. minimizing the pulse duration, and to $$$B_{0}$$$- and $$$B_{1}$$$-robust design of non-selective inversion pulses. The optimized results are investigated numerically and validated by phantom measurements on a 3T MRI system.

Theory

The optimization problem is given as
\begin{align*} &\min J = T + \frac{\alpha}{2}\int \limits_{0}^{T} \left(B_{1}(t)\right)^{2} dt, \\ &\text{s.t.} \: \begin{cases} \left|M_{i,j}(T)-M_{d}\right| < \varepsilon \quad \forall \:i=1, \cdots N,\: j=1, \cdots K, \\ 0\leq B_{1} \leq B_{1,\mathrm{max}}. \end{cases}\end{align*}
Therein, $$$M_{d}=(0,0,-1)^\top$$$ defines the desired state for non-selective inversion and $$$\varepsilon$$$ is allowed absolute error for the inversion efficiency. $$$M_{i,j}(T)$$$ is the solution of the Bloch equations at the terminal time $$$T$$$ for different $$$B_{0}$$$-offsets $$$i=1, \cdots N$$$ and $$$B_{1}$$$-scalings $$$j=1, \cdots K$$$. The last inequality describes the box constraints which limits the maximal RF amplitude with $$$B_{1,\mathrm{max}}$$$. Furthermore, the latter term in the cost functional reduces the power integral with parameter $$$\alpha >0$$$. The full Bloch equations with relaxation effects are solved with symmetric operator splitting¹³. The optimization is based on a trust-region, semi-smooth quasi-Newton method^7,14 and the derivatives are supplied using adjoint calculus.

Methods

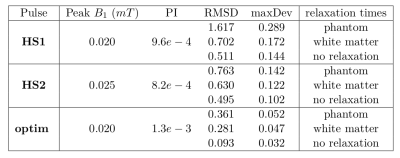
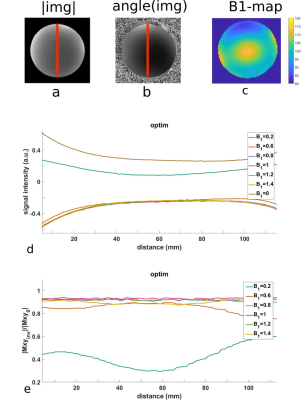
The proposed optimization method designs pulses independent of a sophisticated initial guess due to globalization by a trust-region framework¹⁴. This is demonstrated by choosing a $$$10ms$$$ RF pulse with random magnitude and phase values as an initial. Additionally, for numerical comparison, two adiabatic, hyperbolic-secant RF pulses were designed. The first was a commonly implemented pulse with duration of $$$15.36ms$$$ and bandwith of $$$\Delta f = 10.54kHz$$$ $$$(\textbf{HS1})$$$¹⁵, the second was designed with identical pulse duration ($$$3.28ms$$$) and bandwidth ($$$2.35kHz$$$) as the optimized RF pulse $$$(\textbf{HS2})$$$. The relaxation times were chosen to coincide with the cylindrical phantom used in the experimental validation, $$$T_{1}=102ms$$$ and $$$T_{2}=81ms$$$. We optimized $$$B_{0}$$$-robustness for an offset of $$$\pm 5ppm$$$ at $$$3T$$$ in $$$N=11$$$ steps and simultaneously $$$B_{1}$$$-robustness for $$$70\%$$$ to $$$130\%$$$ in $$$K=9$$$ steps. The numerical evaluation of the optimization was done by means of root-mean-square deviation (RMSD) and maximum deviation (maxDev) for each scaling of $$$B_{1}$$$ and each offset of $$$B_{0}$$$. The optimized RF pulse was implemented on a 3T MRI system (Magnetom Vida, Siemens Healthcare, Erlangen, Germany) as a preparation pulse with $$$TI=6.36ms$$$ in a FLASH sequence ($$$FOV = 300mm, \text{matrix} = 512 \times 256$$$) and validated in two phantom experiments. First, the cylindrical MR phantom was used ($$$TE/TR = 3.3/700ms$$$). Second, a water bottle consisting of $$$400ml$$$ oil and $$$400ml$$$ water with $$$0.2 ml$$$ gadoteric acid resulting in $$$T_{1} = 400ms$$$ was used ($$$TE/TR = 4.9/1500 ms$$$). Additionally, for the cylindrical phantom, we performed a double-angle-measurement¹⁶ for analyzing variations within the $$$B_{1}$$$-field.

Results and Discussion

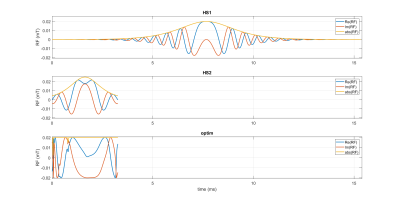
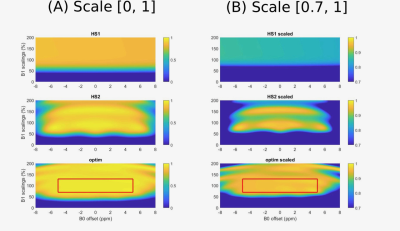
Figure 1 depicts all RF pulses, whereby the pulse duration of $$$\textbf{optim}$$$ was reduced from initially $$$10ms$$$ to $$$3.28ms$$$. The optimized RF exhibits a larger power integral, Table 2, since the RF magnitude is on its box constraint introduced during optimization nearly everywhere, Figure 1. On the other hand, $$$\textbf{optim}$$$ exhibits a heavily increased inversion efficiency with reduction in RMSD and maxDev by a factor of two to three compared with $$$\textbf{HS2}$$$ and five to six compared with $$$\textbf{HS1}$$$ for phantom relaxation times. All pulses show increased inversion efficiency for white matter and without relaxation both in RMSD and maxDev, Table 2. This was expected as relaxation is known to influence simulation results¹³. Figure 3 depicts the inversion efficiency for all RF pulses over a broader set of $$$B_{0}$$$- and $$$B_{1}$$$-variations. The optimized RF pulse (bottom line) performs well within the optimized range of $$$B_{0}$$$- and $$$B_{1}$$$-values (red box). $$$\textbf{HS1}$$$ (top line) shows an evenly distributed inversion performance when reaching the $$$B_{1}$$$-threshold around $$$75 \%$$$ of $$$B_{1}$$$. This coincides with the large bandwidth of it, however, the efficiency itself is not as good as with the others. The optimized pulse $$$\textbf{optim}$$$ was validated in phantom measurements, Figure 4. For a $$$B_{1}$$$-scale of $$$80\%$$$ to $$$120 \%$$$, the pulse inverts magnetization with efficiency of more than $$$90\%$$$ (see part e). Figure 5 shows the same experiment with the water bottle containing oil and water. Again, for a scale of $$$80\%$$$ to $$$120 \%$$$, the inversion efficiency is more than $$$90\%$$$ (part e). Hence, the inversion efficiency is good for oil as well with a frequency offset of $$$3.4ppm$$$, underlining the $$$B_{0}$$$-robustness of the presented RF pulse.

Conclusion

Non-selective and time-optimal inversion pulses were designed by robust optimal control over a defined set of $$$B_{0}$$$- and $$$B_{1}$$$-variations. The inversion efficiency and robustness were validated in extensive phantom measurements. A consequent future development will be the simultaneous control of the gradient for slice-selective pulses.

Acknowledgements

No acknowledgement found.

References

¹Composite RF Pulses for B1+-insensitive volume excitation at 7 Tesla. Moore J, Jankiewicz M, Zeng H, Anderson A.W, Gore J.C. J Magn Reson 2010;205:50--62.

²Handbook of MRI Pulse Sequences. Bernstein M.A, King K.F, Zhou X.J. Elsevier Academic Press, 2004.

³Symmetric pulses to introduce arbitrary flip angles with compensation for RF inhomogeneity and resonance offsets. Garwood M, Ke Y. J Magn Reson 1991;94:511-525.

⁴Recommended Implementation of Arterial Spin-Labeled Perfusion MRI for Clinical Applications: A Consensus of the ISMRM Perfusion Study Group and the European Consortium for ASL in Dementia. Alsop D.C, Detre J.A, Golay X, Günther M, Hendrikse J, Hernandez-Garcia L, Lu H, MacIntosh B.J, Parkes L.M, Smits M, van Osch M.J.P, Wang D.J.J, Wong E.C, Zaharchuk G. Magn Reson Med 2014;00:00-00.

⁵Optimization of adiabatic pulses for Pulsed ASL at 7T - Comparison with Pseudo-continuous ASL. Wang K, Shao X, Yan L, Jin J, Wang D. In Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), 2020.

⁶Factors influencing flip angle mapping in MRI: Pulse shape, slice-select gradients, off-resonance excitation, and B0 inhomogeneities. Wang J, Mao W, Quin M, Smith M.B, Todd Constable R. Magn Reson Med 2006;56:463-468.

⁷Magnetic resonance RF pulse design by optimal control with physical constraints. Rund A, Aigner C.S, Kunisch K, Stollberger R. IEEE Trans Med Imaging 2018;37:461-472.

⁸Simultaneous multislice refocusing via time optimal control. Rund A, Aigner C.S, Kunisch K, Stollberger R. Magn Reson Med 2018;80:1416-1428.

⁹Exploring the limits of broadband excitation and inversion pulses. Kobzar K, Skinner T.E, Khaneja N, Glaser S.J, Luy B. J Magn Reson 2004;170:236-243.

¹⁰Optimal control design of preparation pulses for contrast optimization in MRI. Van Reeth E, Ratiney H, Tesch M, Grenier D, Beuf O, Glaser S.J, Sugny D. J Magn Reson 2017;279:39-50.

¹¹BEEEP: B1-robust energy efficient excitation pulses. Van Reeth E, Ratiney H, Beuf O, Kanice S, Glaser S.J, Sugny D. In Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), 2019.

¹²Inversion pulses with B1-robustness and reduced energy by optimal control. Graf C, Aigner C.S, Rund A, Lesch A.J, Stollberger R. In Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), 2020.

¹³Simulation of Bloch and Bloch-McConnell equations - speed and accuracy. Graf C, Rund A, Aigner C.S, Kunisch K, Stollberger R. In Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), 2019.

¹⁴A hybrid semismooth quasi-Newton method for nonsmooth optimal control with PDEs. Mannel F, Rund A. Optim Eng (2020).

¹⁵ Comparison of 2D and 3D single-shot ASL perfusion fMRI sequences. Vidorreta M, Wang Z, Rodriguez I, Pastor M.A, Detre J.A, Fernandez-Seara M.A. Neuroimage 2013;0:662-671.

¹⁶Imaging of the Active B1 Field in Vivo. Stollberger R, Wach P. Magn Reson Med 1996;35:246-251.

Figures

Long hyperbolic-secant RF pulse $$$\textbf{HS1}$$$ (top), short hyperbolic-secant RF pulse $$$\textbf{HS2}$$$ (middle) and optimized RF pulse iteratively designed from a random initial pulse $$$\textbf{optim}$$$ (bottom). $$$\textbf{HS1}$$$ has a pulse duration of $$$T=15.36ms$$$ and a bandwith of $$$\Delta f = 10.54kHz$$$ and $$$\textbf{HS2}$$$ and $$$\textbf{optim}$$$ have a pulse duration of $$$T=3.28ms$$$ and a bandwith of $$$\Delta f = 2.35kHz$$$.

Key features for both hyperbolic secant pulses $$$\textbf{HS1}$$$ and $$$\textbf{HS2}$$$ and of the optimized RF pulse $$$\textbf{optim}$$$. Peak $$$B_{1}$$$ in $$$mT$$$ and the Power Integral (PI). RMSD and maxDev were calculated for three different sets of relaxation times (phantom ($$$T_{1}=102ms, \, T_{2}=81ms$$$), white matter ($$$T_{1}=832ms, \, T_{2}=80ms$$$) and without relaxation).

Inversion efficiency of the long hyperbolic-secant pulse $$$\textbf{HS1}$$$ (top), of the short hyperbolic-secant pulse $$$\textbf{HS2}$$$ (middle) and optimized RF pulse $$$\textbf{optim}$$$ (bottom) simulated with phantom relaxation times for a broad set of $$$B_{0}-$$$offsets in $$$ppm$$$ and $$$B_{1}$$$-scalings in $$$\%$$$. (A) shows an efficiency scale from $$$0\%$$$ to $$$100 \%$$$ and (B) depicts a zoomed in efficiency scale from $$$70 \%$$$ to $$$100 \%$$$. The red boxes in the bottom row depict the area, where the optimization was performed.

Absolute value and angle of the cylindrical MR phantom image measured with a B₁-scaling of 100% (a-b) and the nominal B₁-map (c). The red line shows the position of the line plots depicted in (d) and (e). The signal intensity profile without and with inversion pulse $$$\textbf{optim}$$$ with different B₁-scalings are shown in (d). In (e), the measured normalized signal intensity after application of the inversion pulse by a measurement without inversion is plotted. Thus, the influence of the coil sensitivity distribution and the varying excitation flip angle is eliminated.

Absolute value and angle of the oil-water phantom image measured with a B₁-scaling of 100% (a-b). The red line shows the position of the line plots depicted in (c) and (d). The signal intensity profile without and with inversion pulse $$$\textbf{optim}$$$ with different B₁-scalings are shown in (c). In (d), the measured normalized signal intensity after application of the $$$\textbf{optim}$$$ inversion pulse by a measurement without inversion is plotted. Thus, the influence of the coil sensitivity distribution and the varying excitation flip angle is eliminated.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

3952