3948
Reducing inter-subject variability and improving accuracy of Universal Pulses using standardized (universal) pulses1Paris-Saclay University, CEA, CNRS, BAOBAB, NeuroSpin, Gif-sur-Yvette, France, 2Siemens Healthcare SAS, Saint-Denis, France
Synopsis
Parallel transmission allows flip angle homogenization at ultra-high field. The pulse design process can be made transparent to the user with calibration-free universal pulses (UP) that are designed over a database of field maps. Here a new method is proposed where UPs are designed over a standardized database, i.e. normalized to a reference. During a scan, these standardized UPs (SUPs) are adjusted to the subject through a fast calibration that relies on a linear transformation of the actual B1+ map to the database reference. Adjusted SUPs improve excitation performance and reduce intersubject variability compared to UPs.
Introduction
In parallel transmission (pTX), pulses can either be designed on-the-fly using subject-specific $$$\Delta{B_0}$$$ and $$$B_1^+$$$ brain field maps, or offline with universal pulses (UP)1, designed over a database consisting in a set of $$$\Delta{B_0}$$$ and $$$B_1^+$$$ brain field maps, called pulse design database. UPs allows one to exploit pTX with no scan time overhead (for calibrations), but with a small performance (excitation accuracy) penalty. In this study, a hybrid method is introduced to improve UP performance through a fast subject-specific calibration. In this approach, the $$$B_1^+$$$ maps of the pulse design database are normalized to a reference $$$B_1^+$$$ map. The resulting normalized database provides, virtually, a decreased intersubject variability in $$$B_1^+$$$2. So-called standardized UP (SUP) are then designed over the normalized database by strictly following the offline UP design approach. A final adjustment step which will be detailed in the Theory Section is taking place during the MRI session, and consists in optimizing the respective amplitude and phase of the SUP RF waveform using subject-specific $$$B_1^+$$$ data acquired with a rapid (<10s) scan3-5. The proposed method allows improving the accuracy of the excitation profiles as demonstrated here with GRAPE pulses6 designed for MPRAGE and MP2RAGE sequences. A comparison of T1 maps returned by the adjusted SUP MP2RAGE sequence to the ones returned with the standard CP mode with $$$B_1^+$$$ postprocessing correction is also provided7,8, showing one potential application of SUPs .Theory
Let us consider a pulse design database of $$$\Delta{B_0}$$$ and $$$B_1^+$$$ maps acquired with $$$N_c$$$ transmit coils over $$$N_s$$$ subjects:$$\Delta B_{0,\mathrm{S}:1},B_{1, \mathrm{S}:1}^+,\cdots,\Delta B_{0,\mathrm{S}:N_s}, B_{1,\mathrm{S}:N_s}^+.$$
This pulse design database can be normalized to design a standardized universal pulse (SUP). The first step is to define a reference transmit field $$$B_{1,\mathrm{Ref}}^+$$$, taken here as the average $$$B_1^+$$$ over the database, i.e. for every voxel $$$r$$$:
$$B_{1,\mathrm{Ref}}^+(r)=N_s^{-1} \sum_{i=1}^{N_s} B_{1,\mathrm{S}:i}^+(r).$$
The second step is to compute, for every subject $$$i$$$ of the database, a position-independent $$$N_c\times N_c$$$ calibration matrix $$$L_i$$$ as the least-squares solution to the problem:
$$\min_{L\in\mathbb{C}^{N_c\times Nc}}\sum_r\|B_{1,\mathrm{S}:i}^{+}(r)-L B_{1,\mathrm{Ref}}^+(r)\|_2^2,$$
The standardized transmit field of this subject is then defined in each voxel $$$r$$$ as:
$$ \tilde{B}_{1,\mathrm{S}:i}^+(r)=L_i^{-1}B_{1,\mathrm{S}:i}^+(r),$$
whereas the $$$\Delta{B_0}$$$ map is left unchanged. This operation is repeated for every subject of the database.
A SUP (k-space trajectory $$$k_{\mathrm{SUP}}(t)$$$, RF waveform $$$u_{\mathrm{SUP}}(t)\in\mathbb{C}^8$$$) is then designed offline on the modified, standardized, field database using the usual UP design metric (minimisation of the average FA-normalized RMSE). For every new subject $$$i$$$ then undergoing a new MR exam, a calibration matrix $$$L_i$$$ is determined as:
$$L_i=\min_L \sum_r\|B_{1,\mathrm{S}:i}^+(r)-L B_{1,\mathrm{Ref}}^+(r)\|_2^2,\;\mathrm{subject}\;\mathrm{to}:\forall\;t,\;|L^{-1}u_{\mathrm{SUP}}(t)|<V_{\mathrm{max}},$$
where $$$V_{\mathrm{max}}$$$ is the hardware limit for the RF voltage. The SUP is then adjusted to this subject with the inverse of the calibration matrix:
$$u_{\mathrm{adjSUP}}(t)=L^{-1}u_{\mathrm{SUP}}(t),$$
and (unchanged k-space trajectory):
$$k_{\mathrm{adjSUP}}(t)=k_{\mathrm{SUP}}(t).$$
Since the least squares problem for computing $$$L$$$ is overdetermined ($$$N_c\times{N_c}$$$ complex numbers to fit), the calibration matrix can be estimated from a quantitative $$$B_1^+$$$ mapping protocol offering only a partial coverage (e.g. 3 slices) of the entire volume of interest.
Methods
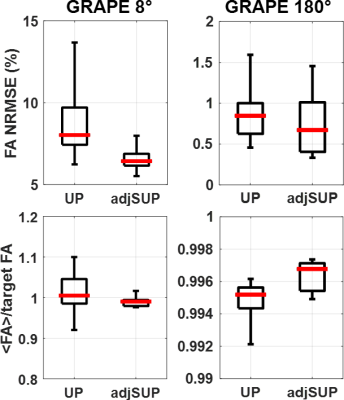
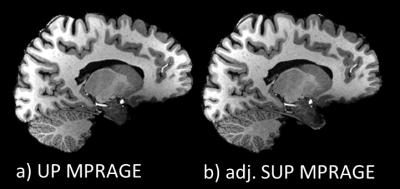
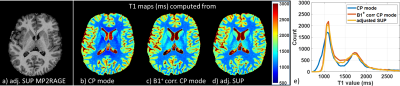
Simulations. A pulse design database with 20 subjects was standardized using the processing steps described above. Nonselective GRAPE UP and SUP were designed offline on this database for the MPRAGE and MP2RAGE sequences (8° excitation and 180° inversion pulses). Excitation performance in terms of fidelity to the target FA of the UP and the adjusted SUP were compared using a test database with 15 subjects.In vivo application. One volunteer was scanned on a Magnetom 7T scanner equipped with the Nova 8Tx-32Rx head coil. Scans included i) a fast $$$B_1^+$$$ map acquired with a 3-slice turbo-FLASH sequence (5mm resolution, TA=10s) ii) two MPRAGE scans using UPs and adjusted SUPs, respectively (TR/TI/TE 2600/1100/2.9ms, resolution 0.8mm, GRAPPA 2, TA 6:51min), and iii) two MP2RAGE scans (adiabatic inversion) using the 8° adjusted SUP and the 8° hard pulse (CP-mode) with TR/TI1/TI2/TE 5000/800/2700/2.84ms, resolution 0.8mm, GRAPPA 3, TA 9:38min. T1 maps were extracted from the MP2RAGE data without and with $$$B_1^+$$$ postprocessing correction7,8.
Results
Flip angle simulations show more homogeneous and accurate with adjusted SUP as compared to UP. This is shown in Figure 1 for the subject scanned in this study (NRMSE of 7.5% and 9.5% respectively for the 8° adjSUP and UP) and on a control database (see Figure 2). A comparison of the MPRAGE images obtained with UP and adjSUP is shown in Figure 3. In Figure 4, the T1 map computed from the adjSUP-MP2RAGE scan without $$$B_1^+$$$ correction is found to be similar to the one computed from the CP-MP2RAGE scan with $$$B_1^+$$$ postprocessing correction.Discussion and conclusion
Adjusted standardized UP allows improving excitation accuracy (reduced FA-NRMSE) thanks to a fast calibration (~10s) scan compared to calibration-less UPs. Additional optimization of the fast 3-slice $$$B_1^+$$$ mapping protocol would allow decreasing further the calibration time. This technique can be used to perform robust quantitative T1 mapping at 7T without additional $$$B_1^+$$$ offline correction. RF pulse design tailored to the subject can remain bypassed for a whole exam. Scans at higher fields, where $$$B_1^+$$$ variability is expected to increase, should benefit even more from this method. Future works include extended in vivo validation.Acknowledgements
This work received financial support from the Leducq Foundation (large equipment ERPT program, NEUROVASC7T project) and from FET-Open H2020 (AROMA project, grant agreement n°885876).References
1. Gras V, Vignaud A, Amadon A, Bihan DL, Boulant N. Universal pulses: A new concept for calibration-free parallel transmission. Magn. Reson. Med. 2017;77:635–643.
2. Gras V, Mauconduit F, Boulant N. A Statistical Robust Approach to Design Parallel Transmit Radiofrequency Excitations in MRI. Concepts in Magnetic Resonance Part A 2020;2020:1–13.
3. Fautz H-P, Vogel M, Gross P, Kerr A, Zhu Y. B1 mapping of coil arrays for parallel transmission. ISMRM 2008.
4. Brunner DO, Pruessmann KP. B 1+ interferometry for the calibration of RF transmitter arrays: B 1+ Interferometry for Array Calibration. Magn. Reson. Med. 2009;61:1480–1488.
5. Amadon A, Cloos MA, Boulant N, Hang M-F, Wiggins CJ, Fautz H-P. Validation of a very fast B1-mapping sequence for parallel transmission on a human brain at 7T. ISMRM 2012.
6. Damme LV, Mauconduit F, Chambrion T, Boulant N, Gras V. Universal nonselective excitation and refocusing pulses with improved robustness to off-resonance for Magnetic Resonance Imaging at 7 Tesla with parallel transmission. Magn. Reson. Med. 2021;85:678–693.
7. Mauconduit F, Massire A, Gras V, Amadon A, Vignaud A, Boulant N. PASTeUR package extension with MP2RAGE for robust T1 mapping technique in parallel transmit at 7T. ISMRM 2020.
8. Massire A, Taso M, Besson P, Guye M, Ranjeva JP, Callot V. High-resolution multi-parametric quantitative magnetic resonance imaging of the human cervical spinal cord at 7T. Neuroimage. 2016;143:58-69.
Figures
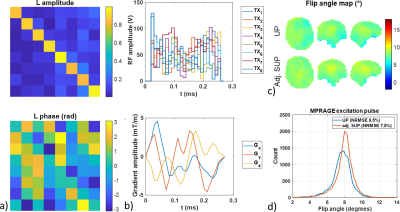
Figure 1: Pulse design methodology in the volunteer for the MPRAGE excitation 8° GRAPE pulse. a) A calibration matrix (L) is computed to adjust the standardized universal pulse (SUP) designed over the standardized pulse design database to the subject B1+ map. Its magnitude is close to the identity matrix while diagonal phase terms are close to 0 radian. b) RF and gradient amplitudes of the resulting adjusted SUP. c and d) Flip angle maps and histograms retrospectively simulated on the subject for the UP and adjusted SUP with the subject’s full B1+ map. NRMSEs are 9.5% and 7.5%, respectively.