Introduction

Significant improvements in polarization levels and speed have expanded the utility of in vivo imaging with hyperpolarized media [1,2]. Unfortunately, the initial longitudinal magnetization, M_z(0), is non-equilibrium and decays due to RF and T₁ relaxation, introducing image artifacts and complicating quantitative analysis [3, 4]. To correct for HP decay, we introduced a method to map M_z dynamics using Bloch-equation-based modeling and radial keyhole image reconstruction [5, 6, 7]. This method was validated in simulations and phantoms and successfully applied to HP ¹²⁹Xe ventilation imaging, However, the impact acquisition and reconstruction strategies on image correction have not been rigorously investigated. Here we develop an analytical approach based on uncertainty propagation to optimize radial keyhole correction of hyperpolarized decay and apply it to human lung imaging with HP ¹²⁹Xe.

Background

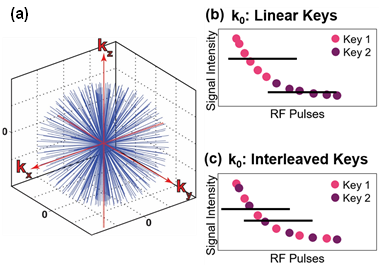
When imaging with center-out trajectories, k₀ (i.e. signal at k-space center) is sampled with each acquisition [8] (Fig. 1a), and image intensity is given by the average of k₀:

(1) $$$S= \frac{1}{N}\sum_{n=1}^NM_z (0) sin⁡(α_{rf}) C_1^{n-1}=\frac{M_z (0)sin(α)}{N} \frac{(1-C_1^N)}{(1-C_1 )} $$$
where (2) $$$ C_1=cos⁡(α) exp⁡(\frac{-TR}{T_1})$$$

and N is the number of views. Because k₀ is sampled with each acquisition, the HP decay term, C₁, is encoded simultaneously with image data (Fig. 1b, c). This decay is intrinsically low frequency information, so Eq. 1 can be separated into K temporally resolved keys. For example, the data can be separated linearly (ie. key 1 = first half of projections, key 2 = second half) or as interleaves (ie. key 1 = even projections, key 2 = odd projections), yielding the signal intensities given by Eq. 3 and Eq. 4, respectively. C₁ can then be extracted for both strategies following Eqs. 5, 6 and decay can be corrected.

(3) $$$S_{κ,L}=M_z (0) sin⁡(α) \frac{C_1^\frac{(κ-1)N}{K}}{N/K}\frac{1-C_1^\frac{N}{K}}{1-C_1}$$$
(4) $$$S_{κ,I}=M_z (0) sin⁡(α) \frac{C_1^\frac{(κ-1)}{K}}{N/K}\frac{1-C_1^N}{1-C_1}$$$
(5) $$$C_{1, L}= ( S_2 /S_1)^{2/N}$$$
(6) $$$C_{1, I}= S_2 /S_1$$$

Image signal can then be corrected—i.e., scaled to yield signal in the absence of magnetization decay, $$$S_0≡M_z (0)sin(α)$$$—by calculating an voxel-by-voxel attention term, A (Eq. 7).

(7) $$$A =\frac{S_0- S}{S_0} = 1-\frac{1}{N}\frac{1-C_1^N}{ 1-C_1}$$$

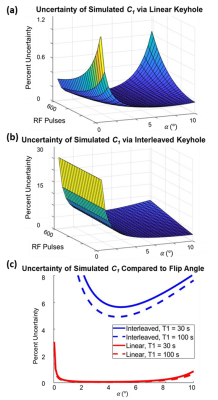
The uncertainty in C₁ is dominated by the signal-to-noise ratio, which depends on acquisition parameters (TR, $$$α$$$, etc.) and noise. Error propagation allows this uncertainty to be modeled a priori for the complete range of experimental values and keyhole methods. Uncertainties for linear (Fig. 2a) and interleaved keyhole (Fig. 2b.) are given in Eqs. 8 and 9, respectively.

(8) $$$σ_{C_{1, L} }= σ_S \frac{2}{N}\frac{C_1}{S_1} \sqrt{1+\frac{1}{C_1^N} }$$$
(9) $$$σ_{C_{1, I} }= σ_S \sqrt{(\frac{-S_2}{S_1^2})^2+(\frac{1}{S_1})^2 }$$$

Methods

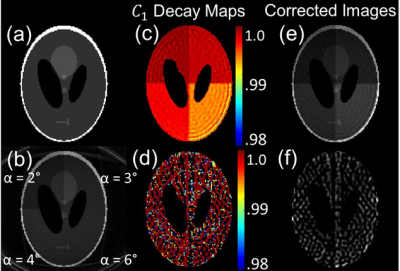
Analytical Simulations: The uncertainty in C₁, $$$σ$$$, was simulated as a function of $$$α$$$, T₁, and number of RF pulses in MATLAB 2018a.
Digital Phantom: A 3D Shepp‐Logan phantom was generated in MATLAB and sampled with 3D radial golden‐angle trajectories, while including HP magnetization decay (Eqs. 1 and 2). Flip angle was varied between 1-10°, T1 = 30 s, N = 410 views, and TR = 5 ms.
Monte Carlo: Digital phantom simulations were repeated with unique Rician noise 30 times to observe C₁ variation. The standard deviation of C₁ for each parameter space was compared to analytical uncertainty.
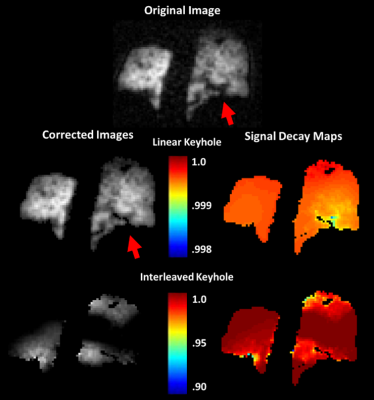
In Vivo Imaging: 3D radial MRI was performed with a 3T Philips Achieva and ¹²⁹Xe polarized to ~40% (Model 9820, Polarean Imaging plc): $$$α$$$ = 1°, TR = 4 ms, TE = 0.118 ms, N =3600 views, BW/pixel = 317.4, FOV = 300 mm.

Results

The predicted uncertainty in signal decay as a function of experimental parameters has a clear minimum (Fig. 2). The appearance of uncertainty minima for both strategies demonstrates that image acquisition parameters directly impact the accuracy of decay correction. Comparison of Fig. 2a and 2b indicates that linear keyhole generates substantially reduced uncertainty.

These analytical trends had good agreement with Monte Carlo simulations (e.g., Fig. 3) over a range of flip angles. For T₁ = 30 s, TR = 5.3 ms, and N = 410 views, the analytical model predicted a minimum uncertainty at $$$α$$$ = 3.6° and 4.6° for linear and interleaved keyhole, respectively. For Monte Carlo simulation, the minimum occurred at similar values of $$$α$$$ = 3.7° and a = 4.2°, respectively. Further, the interleaved keyhole uncertainty values in the Monte Carlo simulations were 10-fold higher than the linear keyhole approach.

When applied to in vivo imaging data (Fig. 4), the C₁ extracted via linear keyhole had low, slowly varying spatial heterogeneity consistent with RF imperfections. In contrast, interleaved keyhole generated physically implausible attenuation values and led to distorted image corrections.

Conclusions

Keyhole correction combined with radial keyhole reconstruction provides a means of correcting HP signal decay without additional data collection. Further, error propagation, when applied to analytical expressions for HP magnetization decay, provides a means to minimize uncertainty, and thus optimize acquisition parameters prior to costly hands-on MRI experiments. Moreover, this analytical approach provides a means of determining the utility of different keyhole reconstruction strategies. Robust corrections were only obtained with the linear method, demonstrating the ability of the analytical approach to meaningfully identify superior keyhole approaches. Because the approach made no assumptions about the nature of the hyperpolarization, this analytical model can be expanded to investigate the impact of reconstruction strategy (e.g., keyhole number) and to other HP nuclei.

Acknowledgements

This study was supported by the NIH (NHLBI R01HL143011).