Introduction

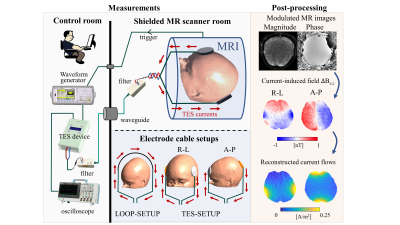
Efficacious use of TES for treating neuropsychiatric disorders or for cognitive enhancement requires the exact knowledge of the current flow induced in the brain. MRCDI uses MRI to measure the magnetic fields created by the TES currents in the head, and reconstructs the current density distribution from these measurements (1). Specifically, the component ∆B_z,c of the TES-induced magnetic field that is parallel to the scanner field modulates the phase of the MR signal. The modulated MR signal can be used for ∆B_z,c calculations and current flow reconstructions (Fig. 1 and 2a) (2). The accuracy of the method highly depends on the sensitivity and spatial resolution of the MRCDI measurements. We have previously reported reliable MRCDI measurements in the human brain with a sensitivity of ~0.1 nT for a ~9 mins scan time (2). Here, we improve our original gradient-echo based MRCDI method by means of an optimized spoiling scheme, acquisition-weighting (AW), and navigators to improve the ∆B_z,c image quality and measurement sensitivity limits at high resolution.

Methods

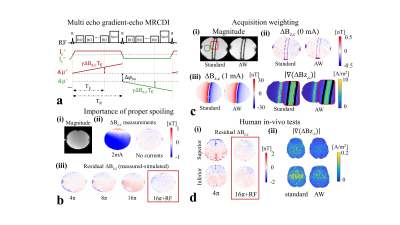
First, we performed MRCDI measurements in a spherical phantom (0.1 mM MnCl₂ + 1.5 g/L NaCl) with the LOOP-SETUP in Fig 1 to optimize spoiling: Field of view FOV = 224×183 mm², imaging matrix 112×92, tip-angle α=30°, echo time T_E = [5.6, 14.4, 23.2, 32, 40.8, 49.6] ms, repetition time T_R=80 ms, the number of measurement repetitions N_meas = 16. The experiments with phase-coherent RF excitations were repeated with four different spoiler gradients to provide intra-voxel phase dispersions of $$$\varphi_{sp}=[4π, 8π, 16π,$$$ and $$$32π]$$$. The experiment with $$$\varphi_{sp}=16π$$$ was then repeated with RF spoiling (phase-cycled RF excitations with 50° increments). Second, we employed a spherical phantom (0.1 mM MnCl₂ + 1.5 g/L NaCl), in which a cylindrical insulating tube (0.1 mM MnCl₂ + 1.5 g/L NaCl + 1 g/L TX151) was placed for current injection, to explore sensitivity gain by means of AW against standard acquisition: FOV = 224×183 mm², α=30°, T_E = [5.6, 14.4, 23.2, 32, 40.8, 49.6, 58.4, 67.2] ms, T_R=80 ms, and $$$\varphi_{sp}=16π$$$ combined with RF-spoiling. a) Standard acquisition: N_meas = 16 was kept fixed for each of the k-space measurements and an image matrix of 112×92 used. b) Acquisition-weighting: The k-space data was acquired in a ~1.6 times broader window and filtered with a Hanning window $$$h(k_x)=\frac{1}{2}(1+cos(\frac{2πk_x∆x}{\beta_w}))$$$ with $$$\beta_w = 1.6$$$ (3). N_meas was varied systematically to match the applied filter in the phase encoding direction and an imaging matrix of 176×144 was used. We also validated the impact of using optimum spoiling and AW by performing human in-vivo experiments with the LOOP-SETUP using the same method parameters in phantoms. Finally, we recruited five subjects to test our improved method’s human in-vivo performance against our original method using the TES-SETUP. Our original method (2) used N_meas = 18, T_R = 80 ms, T_E = [7.5, 19.8, 31.9, 44, 56.2] ms, α=30°, $$$\varphi_{sp}=4π$$$, image matrix 112×90, voxel size 2×2×3mm³ and a chemical-shift-selective fat suppression technique. In our improved method, we acquired extra echoes instead of using fat suppression: T_E = [5.6, 14.4, 23.2, 32, 40.8, 49.6, 58.4, 67.2] ms and image matrix 176×144. The first echo was replaced with a 0-D navigator to assess measurement quality. The optimized spoiling scheme ($$$\varphi_{sp}=16π$$$ with RF-spoiling) and AW were applied similar to the phantom experiments. Both experiments used the same FOV = 224×183 mm² and a matched total scan time of ~4:20 mins for a direct comparison. The experiments were repeated with no currents to measure noise floors and with 1 mA currents injected in the right-left and anterior-posterior directions.

Results and discussions

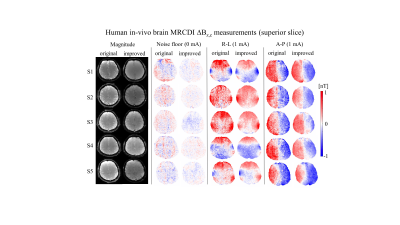
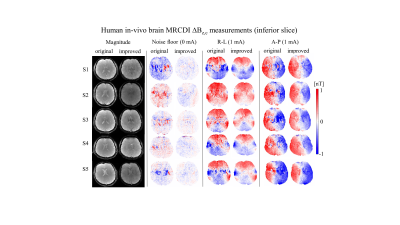
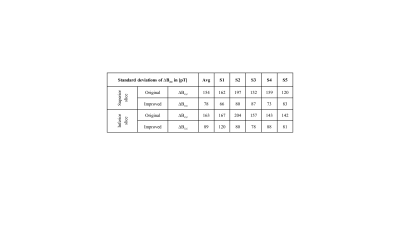
MR magnitude images of the phantoms in Figure 2b,c are artifact-free and the ∆B_z,c spatial distributions are as expected. Interestingly, increasing the spoiler gradients changes the residual ∆B_z,c images (difference between the measured and simulated ∆B_z,c calculated from the delineated cable paths by using the Biot-Savart law (4)). Visual inspection demonstrates two distinct spatial components, one corresponding to the current-induced field and the other to $$$T_2^*$$$. The suggested spoiling scheme ($$$\varphi_{sp}=16π$$$ with RF-spoiling) effectively minimizes the residuals. Using AW significantly improves the quality of ∆B_z,c and its normalized gradient |∇(∆B_z,c)| images (Fig. 2c) and resolves ringing artifacts well. The results translate well to in-vivo (Fig. 2d). Figure 3 and 4 show ∆B_z,c measurements for a superior and an inferior slice. The SNR and image quality greatly improve, and severe artifacts near ventricle regions are resolved by our improved method. On average across the five subjects, the improved method exhibits an almost two-fold sensitivity increase over our original method, with noise standard deviations in the ∆B_z,c images being as low as 78 pT in the superior and 89 pT in the inferior slices for a total scan time of 4:20 mins (Table 1).

Conclusion

Our improved method boosted the sensitivity and spatial resolution of MRCDI measurements, and it is thus promising for accurate measurements of TES currents in the brain. Future studies will explore further methodological improvements that can allow for current flow reconstructions in a 3D volume.

Acknowledgements

The project is supported by Lundbeck foundation with grant numbers R288-2018-236 and R244-2017-196.