Introduction

Electrical properties tomography has proven benefits in clinical, oncologic studies [1]. The phase-based electrical properties method is a feasible approach that retrieves the conductivity images using MR transceive phase data [2]. In the MR scanning for the transceive phase image, the MR magnitude image can be obtained simultaneously. The magnitude images contain structural information. However, it does not be used in conductivity reconstruction. Thus, exploiting the information could improve conductivity imaging. In this study, we proposed a new prior model to incorporate anatomical information into the gradient-based conductivity imaging method.

Theory

The central equation of gradient-based electrical conductivity imaging method is as follows [2]:
$$\triangledown\phi\cdot\triangledown\rho+\triangledown^{2}\phi\rho-2\omega \mu_{0}=0$$
Where $$$\rho=1/\sigma$$$, $$$\omega$$$ is angular frequency and $$$\mu_{0} $$$ is magnetic permeability in free space. The discretized Equation (1) in an imaging region can be converted into an inverse problem using the first-order central differential scheme, which is $$$A\rho=b$$$. To solve this problem, we perform conductivity reconstruction via minimization of an objective function:
$$\widehat{\rho}=argmin_{\rho}\frac{1}{2}\parallel A \rho-b \parallel_2^2+\alpha\left(J\left({\rho}\right)\right)$$
Where $$$J\left({\rho}\right)$$$ is the regularization term that enforces prior knowledge, $$$\alpha$$$ is the regularization parameters. We define a prior that extract the Structural Similarity between conductivity and MR magnitude image [3-4], the prior model is expressed as:
$$J\left({\rho}\right)= \parallel\langle D\left(v\right),\triangledown{\rho}\rangle\parallel_1$$
Where $$$v$$$ is the MR magnitude image.
$$D_x\left({v}\right)=\sum_{q\in R\left(p\right)} g_{p,q}\cdot\mid\left(\partial_{x}v_q \right)\mid$$
$$D_y\left({v}\right)=\sum_{q\in R\left(p\right)} g_{p,q}\cdot\mid\left(\partial_{y}v_q \right)\mid$$
where $$$R\left(p\right)$$$ is the region that centered in $$$p$$$. $$$g_{p,g}$$$ is a weighting function defined according to spatial distance, expressed as:
$$g_{p,g}\propto exp\left(-\frac{\left(x_p-x_q\right)^2 +\left(y_p-y_q\right)^2}{2\xi^2}\right)$$
where $$$\xi$$$ controls the spatial scale of the window, $$$x_p$$$, $$$y_p$$$ are the horizontal and vertical coordinates of pixel $$$v_p$$$, $$$x_q$$$, $$$y_q$$$ are the horizontal and vertical coordinates of pixel $$$v_q$$$; $$$p$$$, $$$q$$$ index the image pixels. The prior can extract the meaningful structure from the MR image in a local window. The optimal optimization is solved by the alternating direction method of multipliers (ADMM) method [5].

Method

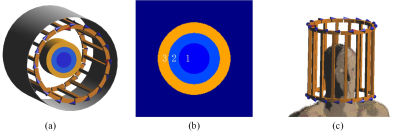
The complex $$$B_1^+$$$ filed was simulated using a Finite-Difference Time-Domain (FDTD) based software (SEMCAD X. 14.6, Zurich Switzerland). Figure 1 shows the simulation setup; it contains the quadrature birdcage coil, cylindrical phantom and human brain model (Duke Model, Virtual family). The cylindrical phantom includes three parts to mimic brain tissues: white matter, grey matter and Cerebrospinal fluid (CSF), as shown in Figure 1(b). The simulation was performed at 128MHz (3T) and then the phase of $$$B_{1}^{+}$$$ and $$$B_{1}^{-}$$$ was added to get transceive phase.

The MR magnitude image was emulated in Matlab (The MathWorks, Inc., Natick, MA) using a Bloch simulator [6]. The input for the simulation was the geometry of the cylindrical phantom, the $$$B_{1}^{+}$$$ amplitude map from electromagnetic simulation and the T1 and T2 maps. The SE sequence was simulated for this study, and the T1-Weighted image was obtained by adjusting the TR and TE parameters. Then the magnitude images were used to construct the prior.

The proposed method was compared with the conventional method (referred to as CM ), which is based on the homogenous assumption, and the double regularization method(referred to as DRM ), whose regularization terms contain total variation and wavelet transform.

Results

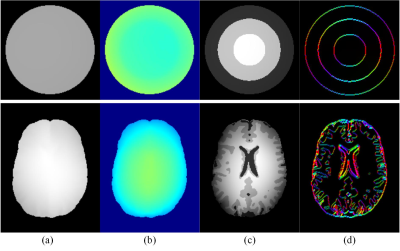
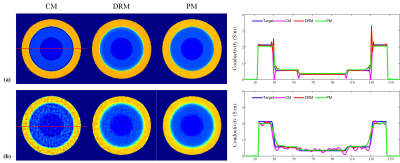
Figure 2 shows the simulation images of cylindrical phantom and head model, figure 2(a) is the magnetic image of $$$B_{1}^{+}$$$ and figure 2(b) is the transceive phase. Figure 2(c) depicts the simulated MR magnetic images and figure 2(d) is the directional structure information $$$D_x$$$ and $$$D_y$$$.
The reconstructed conductivity maps of the cylindrical phantom are shown in Figure 3. Figure 3(a) shows the results obtained from noise-free data. The profile of the proposed method is matched with the target profile. Figure 3(b) presents the conductivity under the noise condition; the proposed method describes the accurate results than other methods.
Figure 4 shows the results of the human brain model. Figure 4(a) is the conductivity distribution without noise contamination. Figure 4(b) magnifies the block areas in figure 4(a). The results of the proposed method preserve more details than conventional and double regularization methods. Figure 4(c) is the result under noise conditions; the conductivity of the proposed method shows the clearer structure, which indicates that the proposed method improves the accuracy of the conductivity imaging.

Discussion and Conclusion

In the implementation of conductivity imaging, the MR magnitude image is obtained when get the transceive phase image. The magnitude image contains the structure information of the object. Thus, we defined a new prior model to extracting the structure information to improve the conductivity reconstruction. The proposed method exploits the anatomical information to preserve more detail and reduce the effect of noise. The simulation of the cylindrical phantom and head model was used to validate the superiority of the proposed method. However, in the calculation of the proposed method, some parameters need to be set. Thus a method that parameters determined automatically should be done. The MR magnitude image simulation was performed for the SE sequence because it is easy to simulate and is common in clinical applications.

Acknowledgements

This work was supported by the Key-Area Research and Development Program of Guangdong Province under Grant 2018B030333001, the National key research and development program under grant 2016YFC0104003, the Natural Science Foundation of Guangdong Province under grants 2016A030313577, and the Program of Pearl River Young Talents of Science and Technology in Guangzhou under grant 201610010011.