Introduction

High-field MRI has many well-known advantages compared with MR imaging at lower field strengths. The (theoretical) signal to noise ratio, for example, is much higher and allows for fast high-resolution imaging. It also enables imaging of nuclei different from the typical hydrogen nucleus.
A consequence of using high background fields is that the Larmor frequency also increases, from a frequency of approximately 300MHz at 7T up to 600MHz for the newest 14T (human bore) scanners. The object inside the scanner can then no longer be considered much smaller than the wavelength, which decreases proportionally (and is 1m in free space at 7T).
Until recently, the influence of high-frequency scattering has not been investigated in the context of MR signal modeling. In[1], however, we have presented signal models in which scattering effects are taken into account. Our full-wave field analysis is based on Maxwell's equations and can be used to obtain signal representations in a wide variety of measurement scenarios.
In this abstract we focus on signal models for magnetic and electric dipole measurements. In particular, for a homogeneous sphere we explicitly show how its conductivity and permittivity influence the recorded signal that is obtained by carrying out a loop antenna measurement. Furthermore, we demonstrate that in high-field MRI these parameters may even be retrieved from free induction decay (FID) signals that are measured by an electric or magnetic dipole.

Methods

Using the linearity of Maxwell's equations, signal models that include dielectric scattering effects can be obtained. These models can be derived for fairly general measurement scenarios[1], but here we focus on magnetic (EMF) and electric (MMF) dipole measurements. The models consist of a direct term due to the time-varying magnetization and a term that is due to the electric scattering currents inside the object. In principle, these currents can be determined if the conductivity and permittivity profiles are known by solving a forward problem for the electric field. Under certain conditions, however, the Born approximation[2] may be applied, which consists of approximating the electric field inside the object by the background field. Assuming that this approximation holds for a homogeneous sphere with constant dielectric parameters and uniform excitation, the voltage signal (EMF) that is measured by a small loop located outside the sphere is[1]
$$ d_h(t) = \partial_t\vec{M}(t)\cdot\vec{a}_1 + \frac{\sigma}{3}\mu_0\partial_t^2\vec{M}(t)\cdot\vec{a}_2 + \frac{\varepsilon_r-1}{3}c_0^{-2}\partial_t^3\vec{M}(t)\cdot\vec{a}_3,\qquad(1)
$$
where travel times have been ignored. Here, $$$\vec{M}$$$ is the magnetisation, $$$\sigma$$$ the conductivity, $$$\varepsilon_r$$$ the relative permittivity. The spatial weighting vectors $$$\vec{a}_{1,2,3}$$$ depend on the antenna location and its size.The temporal derivatives of the magnetisation lead to polynomial dependence between signal and Larmor frequency, where the quadratic and cubic coefficients depend on the conductivity and permittivity, respectively. This seems to be in agreement with recent work in electrical properties tomography, where the conductivity is considered more relevant at lower frequencies, whereas the permittivity starts playing a role at high frequencies [3]. For electric dipole measurements a similar representation may be derived [1], but the dependence of the resulting signal on the conductivity/permittivity is different. Knowing this explicit dependence allows reconstructing the electric properties from measured signals.

Experiments

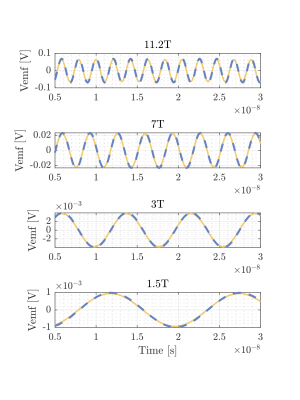
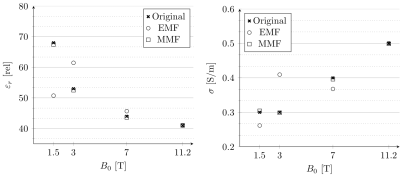
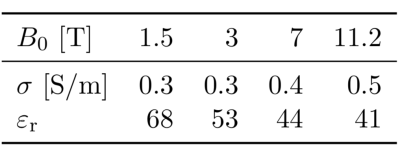
For FID signals the magnetization is known, and we validate the Born approximation for a sphere by comparing the EMF-FID signal of (1), which is based on the Born approximation, with the signal computed with an in-house FDTD simulation package. The receiver is located at the surface of the sphere and is oriented such that its normal is directed in the radial direction away from the sphere. The sphere has a diameter of 5cm and consists of uniform white matter tissue with frequency-dependent dielectric parameter values as listed in Table (1). Second, the same sphere is used to reconstruct its electrical properties ($$$\sigma,\varepsilon_r$$$) from measured EMF- and MMF-FID signals obtained at various field strengths. To this end, we store time samples of the measured signal in a vector $$$\vec{d}$$$ and add noise to the data (SNR is 20 dB). Subsequently, for EMF-FID signals we use (1) to setup a linear system $$$\vec{d} = \mathrm{A}\vec{c}$$$, where $$$\mathrm{A}$$$ contains the spatial weighting and magnetisation components and $$$\vec{c}={[\sigma, \varepsilon_r-1]}^T$$$. This system is solved using the LSQR algorithm. For MMF-FID signals, a similar approach is followed.

Results

Figure (1) gives a comparison between our Born-based EMF-FID model (1) and a full FDTD simulation for a homogeneous sphere. In Figure (2) the mean reconstruction results for various frequencies and both antenna types (EMF and MMF) can be found.

Discussion and Conclusion

Through a scattering formalism signal models can be obtained which take dielectric scattering effects into account. For a homogeneous sphere for which the Born approximation holds, these models explicitly show how the dielectric parameters influence measured dipole signals and allow straightforward reconstruction of these parameters from the measured dipole signals. Which parameter can be reliably retrieved depends on the type of measurement and the strength of the background field. Further validation using in-vivo MRI experiments is still needed. Additional examples of applications for the comprehensive signal model are antenna and pulse sequence design, specifically for electrical properties imaging (or to minimise the influence of these), SNR optimisation, or minimising local specific absorption rate.

Acknowledgements

No acknowledgement found.