INTRODUCTION

Electric properties tomography (EPT) is a quantitative imaging technique based on MRI conceived to measure, in a non-invasive way, the electric properties (EPs), conductivity $$$\sigma$$$ and permittivity $$$\varepsilon$$$, of human body tissues. Despite being a relatively novel technique, a plethora of methods^1,2,3,4,5 have been proposed for its practical implementation.
EPTlib⁶ is an open-source C++ library shared on github, that collects EPT methods to facilitate their comparison and to attract new scientists, that could be discouraged by the large number of proposed methods, to contribute in EPT development.
Three methods are currently implemented in EPTlib: Helmholtz-EPT (H-EPT),¹ convection reaction–EPT (CR-EPT)^2,3 and gradient-EPT (G-EPT).⁴ However, the design of the library is such that it can be easily extended by implementing new methods.

SOFTWARE ARCHITECTURE

The EPT methods are implemented in EPTlib as C++ classes derived from a common abstract class collecting the basic features of EPT methods. The abstract class guarantees that all implemented methods receive the transmit sensitivity and/or the transceive phase, solve the reconstruction problem and return the conductivity and/or permittivity according to the same set of rules. The option to post-process the results by applying a median filter, whose window is possibly deformed according to the anatomical geometry of the tissues in a reference image, is managed by the abstract class, as well.
Along with the C++ library, EPTlib comes with a console application that allows to run all the methods implemented in the library. The application is set-up by a configuration file in toml format and handles binary input and output files in hdf5 format.

IMPLEMENTED METHODS

H-EPT¹ retrieves the EPs according to$$\varepsilon-\text{i}\frac{\sigma}{\omega}=-\frac{\nabla^2B_1^+}{\omega^2\mu_0B_1^+}\,,$$where $$$\omega$$$ is the angular frequency, $$$\text{i}$$$ is the imaginery unit, $$$\mu_0$$$ is the magnetic permeability of vacuum and $$$B_1^+$$$ is the measured complex transmit sensitivity, whose phase is approximated by half the transceive phase $$$\varphi^\pm$$$. If only the transmit sensitivity $$$|B_1^+|$$$ or the transceive phase are provided to EPTlib, the magnitude- or phase-based approximation of H-EPT¹$$\varepsilon=-\frac{\nabla^2|B_1^+|}{\omega^2\mu_0|B_1^+|}\,,\quad\text{and}\quad\sigma=\frac{\nabla^2\varphi^\pm}{\omega\mu_0}\,,$$is applied to retrieve one EP.
CR-EPT² estimates the EPs by solving the partial differential equation (PDE) in conservative form$$\nabla\cdot\left(\gamma\left(\nabla{}B_1^+-\text{i}\nabla\times(B_1^+\hat{z})\right)\right)=-\omega^2\mu_0B_1^+\,,$$where $$$\gamma=(\varepsilon-\text{i}\sigma/\omega)^{-1}$$$ is the unknown and $$$z$$$ is the longitudinal direction. The PDE is solved numerically with a second order finite difference scheme. An artificial diffusion term can be added to stabilize the procedure. If only the transceive phase $$$\varphi^\pm$$$ is provided to EPTlib, the phase-based approximation of CR-EPT³ is applied. The approximation solves, with a stable numerical method based on an upwind finite difference scheme, the real-valued PDE$$\nabla\cdot\left(\rho\nabla\varphi^\pm\right)=2\omega\mu_0\,,$$where $$$\rho=\sigma^{-1}$$$ is the unknown. Artificial diffusion can be introduced as a further stabilization. If the longitudinal variation of the EPs is negligible, the computational burden can be reduced by solving the PDE in two dimensions.
G-EPT⁴ is implemented in two steps. First, the gradient of the logarithm of the EPs, $$$\boldsymbol{g}=\nabla\text{log}(\varepsilon-\text{i}\sigma/\omega)$$$, is computed by solving for each voxel a linear system of equations like$$-\text{i}2\nabla{}B_{1,i}^{+,\text{r}}\cdot\nabla\varphi^+_0+\nabla{}B_{1,i}^{+,\text{r}}\cdot\left(g_+,-\text{i}g_+,g_z\right)+B_{1,i}^{+,\text{r}}\vartheta^+=\nabla^2B_{1,i}^{+,\text{r}}\,,$$with respect to the unknowns $$$\nabla\varphi_0^+$$$, $$$g_+$$$, $$$g_z$$$ and $$$\vartheta^+$$$. In the latter, $$$\varphi^+_0$$$ is the reference transmit phase, $$$B_{1,i}^{+,\text{r}}=|B_{1,i}^+|\text{exp}(\text{i}(\varphi_i^\pm-\varphi_0^\pm))$$$ is the measurable part of the transmit sensitivity of the $$$i$$$-th transmit channel, $$$g_+=g_x+\text{i}g_y$$$ and $$$\vartheta^+=-\omega^2\mu_0(\varepsilon-\text{i}\sigma/\omega)+|\nabla\varphi_0^+|^2-\text{i}\nabla^2\varphi_0^++\text{i}\nabla^2\varphi_0^+\cdot(g_+,-\text{i}g_+,g_z)$$$. Then, the gradient is inverted by solving the minimization problem$$\varepsilon-\text{i}\frac{\sigma}{\omega}=\text{argmin}_u\left(\|g_+[u]-g_+\|^2+\|g_z[u]-g_z\|^2\right)\,,$$with the EPs constrained to a given value in a seed point selected by the user. The minimization is performed by solving the associated Euler equation with the finite element method. Also in this case the computational cost can be reduced by solving the problem in two dimensions. The implementation of G-EPT in EPTlib is still under development in order to remove the need of a seed point selected in advance by the user.
For all the implemented methods, the spatial derivatives are evaluated using the Savitzky-Golay filter⁷ with a kernel whose shape and size are arbitrarily chosen by the user. All the methods accept only one receive channel, whilst G-EPT needs more than 4 transmit channels.

EXAMPLE OF USAGE

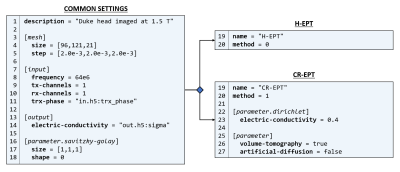
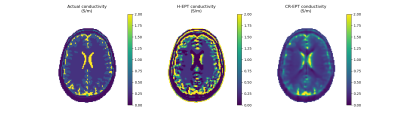
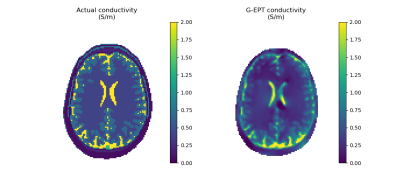
The implemented methods are tested on noiseless virtual measurements obtained by simulating the head of Duke⁸ radiated by a 1.5 T low-pass body coil and a 7 T 8-channel head coil. H-EPT and CR-EPT are applied with phase-approximation to the 1.5 T data according to the configuration files in Figure 1. CR-EPT has more operative parameters than H-EPT, precisely the boundary condition $$$\sigma=0.4$$$ S/m (skin conductivity), the choice of a three-dimensional evaluation and the absence of artificial diffusion. The results are shown in Figure 2. G-EPT is applied to the 7 T data according to the configuration file in Figure 3, where a two-dimensional reconstruction is selected and a seed point is defined. Figure 4 reports the result. Savitzky-Golay filter is applied on a minimal cross-shaped kernel for all the methods.

CONCLUSION

EPTlib is a newborn library with the ambition of growing to collect all the EPT methods proposed in literature. Contributors are welcomed to join in EPTlib development.

Acknowledgements

The results here presented have been developed in the framework of the 18HLT05 QUIERO project. This project has received funding from the EMPIR programme co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation programme.