3763
Diffusional Kurtosis Imaging in the Diffusion Imaging in Python Project1Champalimaud Research, Champalimaud Centre for the Unknown, Lisbon, Portugal, 2Cognition and Brain Sciences Unit, University of Cambridge, Cambridge, United Kingdom, 3Department of Physics and Chemistry “Emilio Segrè”, University of Palermo, Palermo, Italy, 4Institute for Learning and Brain Science and Department of Speech and Hearing, University of Washington, Seattle, WA, United States, 5Department of Psychology and eScience Institute, The University of Washington, Seattle, WA, United States, 6Department of Intelligent Systems Engineering, Luddy School of Informatics, Computing and Engineering, Indiana University Bloomington, Bloomington, IN, United States, 7Department of Pediatrics and Graduate School of Education, Stanford University, Stanford, CA, United States
Synopsis
Diffusion Kurtosis Imaging (DKI) estimates non-Gaussian diffusion in biological tissue from diffusion-weighted MRI, providing a useful marker for individual differences in tissue microstructure. We present a well-tested, well-documented open-source implementation of DKI as part of the DIPY (Diffusion Imaging in Python) project. The implementation provides standard DKI metrics, as well as extensions of the method for microstructure modeling and tractography. We demonstrate the use of these methods in openly available datasets.
Introduction
Diffusion Kurtosis Imaging (DKI) estimates non-Gaussian water diffusion in biological tissue1. These estimates are of interest because they were shown to better relate to microstructural alterations in health and diseases2,3 than measures based on the total anisotropy of diffusion which are highly confounded by tissue dispersion and fiber crossings4,5. Despite that DKI has significant relevance in both research and clinical applications, there is no free, and open-source implementation of the algorithms which limits the reproducibility of DKI results across studies. In this work, we implemented DKI in the Diffusion in Python project6 - a large collaborative open-source project which aims to provide well-tested, well-documented and comprehensive implementation of different dMRI techniques. We provide several extensions of the method that together provide a comprehensive toolbox for DKI analysis.Methods
DKI was implemented as part of the DIPY project6, relying on components of the scientific Python ecosystem7,8. The implementation provides standard DKI metrics, as well as several extensions: (1) an isotropic kurtosis index that is robust to noise and invariant to confounding effects due to tissue dispersion -- mean signal DKI (MSDKI)9; (2) a previously proposed DKI-based White matter Tract Integrity (WMTI) microstructural model for coherent fiber structures10; and 3) MSDKI-derived calculations that are equivalent to recently proposed spherical mean technique models (SMT)9,11. The DIPY implementation also includes DKI-based reconstruction of orientation distribution functions (ODFs) that can be used for tractography12,13.The software is tested using pytest and continuous integration. Detailed examples are provided in the DIPY documentation. We use numerical simulations for testing, and for demonstrating the properties of DKI metrics. To further demonstrate the use of our implementations, we analyzed an openly available dataset designed for evaluation of DKI methods14. This dataset was pre-processed using state-of-the-art algorithms already implemented in DIPY such as the Marcenko-Pastur PCA denoising15 and the sub-voxel pixel Gibbs artefact suppression algorithm16. Moreover, we use our implementations with cross-validation17 to assess how well DKI represents the diffusion data of a large sample from the Human Connectome Project18.
Results
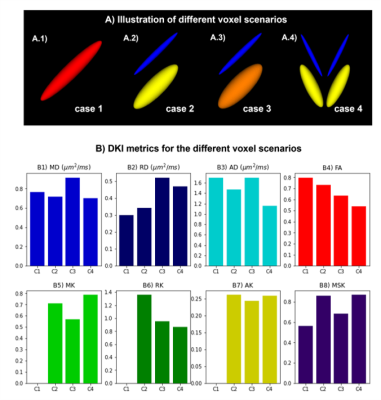
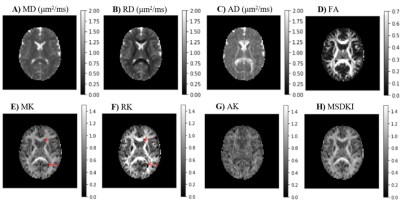
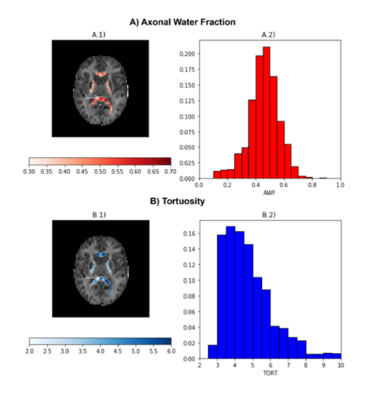
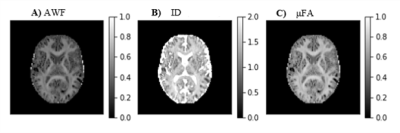
DKI provides information about both diffusion and kurtosis tensors. We demonstrate this with the DIPY implementation, using numerical simulations of several different tissue configurations (Fig. 1). While standard diffusion fractional anisotropy estimates show higher decreases when crossing fibers are incorporated into the simulations (Fig. 1D), standard mean kurtosis (MK) shows higher decreases when the radial diffusivity of simulations compartment 2 is increased (Fig. 1E). To note that the novel MSDKI index is invariant to added crossing compartments (Fig. 1H). We also demonstrate the spatial distribution of DKI metrics in the brain (Fig. 2), showing in particular that the MSDKI index provides low contrast between white matter regions with different white matter fiber dispersion degrees (Fig. 2H) and it is more robust to noise than the standard MK (Fig. 2E).We implemented two microstructure models that extend DKI. Fig. 3 shows the parametric maps and estimated histograms of the axonal volume fraction (AWF) and extracellular tortuosity computed from the white matter tract integrity model (WMTI) - histograms show similar value ranges than reported on the original WMTI paper10. Fig. 4 shows the SMT parametric maps computed from kurtosis estimates - SMT's AWF and microscopic fractional anisotropy (μFA) estimates (Fig. 2A and Fig. 2C) present a similar contrast than MDSKI maps (Fig. 3H).
In the Human Connectome Project dataset, we demonstrate that our DKI implementation represents diffusion-weighted signals more accurately than DTI (Fig. 5).
Discussion
An openly available, well-tested and well-documented implementation of DKI provides a resource and reference for further work with this technique. For users of the method in science applications, it provides an easy-to-install and easy-to-use way to leverage the advantages of DKI in their datasets.Our analysis demonstrates some important properties of DKI-based estimates. Particularly, they confirmed that MK and MSDKI are less affected by confounded tissue dispersion and crossing effects than standard estimates of diffusion anisotropy (Fig. 1 and Fig. 2). The similar contrast between the SMT and MSDKI estimates (Fig.3) confirms that SMT AWF and μFA estimates are just a normalized quantity of diffusion non-Gaussian diffusion degree9. Therefore, in future studies, SMT measures cannot be interpreted as accurate biophysical estimates of axonal water fraction and tissue microscopic anisotropy - instead they should be only used as normalized measures of the degree of non-Gaussian diffusion (with estimates ranging in a scale from 0 to 1).
Our analysis of HCP data demonstrates the utility of adopting DKI in datasets such as the HCP.
Conclusions
DKI in DIPY provides a well-tested, well-documented and comprehensive reference implementation for DKI. For methods developers, our implementation provides a reference framework that can be easily extended to incorporate other novel DKI advances or even its expansion to microstructural modeling or tractography. Moreover, our implementations provide a platform for wider use of DKI in research on brain disorders and cognitive neuroscience research. It will ease the translation of DKI advantages into clinical applications.Acknowledgements
DIPY development is supported through NIH grant 5R01EB027585-02 to Eleftherios Garyfallidis and Ariel Rokem. AR and JK are also supported through 1RF1MH121868-01 from the National Institutes for Mental Health/The BRAIN Initiative and through grants from the Gordon and Betty Moore Foundation and the Alfred P. Sloan Foundation to the University of Washington eScience Institute Data Science Environment, as well as support from the Washington Research Foundation to eScience and to the University of Washington Institute for Neuroengineering. The International Neuroinformatics Coordination Facility supported a research visit by RNH to work on DKI in DIPY.References
1. Jensen JH, Helpern JA, Ramani A, et al. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med. 2005; 53: 1432–1440 (2005).
2. Falangola MF, Jensen JH, Babb JS, et al. Age-related non-Gaussian diffusion patterns in the prefrontal brain. J. Magn. Reson. Imaging 2008; 28: 1345–1350.
3. Cheung JS, Wang E, Lo EH, Sun PZ. Stratification of heterogeneous diffusion MRI ischemic lesion with kurtosis imaging: evaluation of mean diffusion and kurtosis MRI mismatch in an animal model of transient focal ischemia. Stroke 2012; 43: 2252–4.
4. Jones DK, Knosche TR, Turner R. White matter integrity, fiber count, and other fallacies: The do’s and don’ts of diffusion MRI. NeuroImage 2013: 73; 239–254.
5. De Santis S, Drakesmith M, Bells S, et al. Why diffusion tensor MRI does well only some of the time: Variance and covariance of white matter tissue microstructure attributes in the living human brain. NeuroImage 2014; 89: 35–44.
6. Garyfallidis E, Brett M, Amirbekian B, et al. Dipy, a library for the analysis of diffusion MRI data. Front. Neuroinform. 2014; 8: 8.
7. Harris CR, Millman KJ, van der Walt SJ, et al. Array programming with NumPy. Nature 2020: 585; 357–362.
8. Virtanen P, Gommers R, Oliphant TE, et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 2020; 17: 261–272.
9. Henriques RN, Jespersen SN, Shemesh N. Microscopic anisotropy misestimation in spherical-mean single diffusion encoding MRI. Magn. Reson. Med. 2019; 81: 3245–3261.
10. Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. Neuroimage 2011; 58: 177–188.
11. Kaden E, Kelm ND, Carson RP, et al. Multi-compartment microscopic diffusion imaging. Neuroimage 2016; 139: 346–359.
12. Henriques RN, Correia MM, Nunes RG, Ferreira HA. Exploring the 3D geometry of the diffusion kurtosis tensor—Impact on the development of robust tractography procedures and novel biomarkers. Neuroimage 2015; 111: 85–99.
13. Jensen JH, Helpern JA, Tabesh A. Leading non-gaussian corrections for diffusion orientation distribution function. NMR Biomed. 2014; 27: 202–211.
14. Hansen B, Jespersen SN. Data for evaluation of fast kurtosis strategies, b-value optimization and exploration of diffusion MRI contrast. Sci Data 2016; 3: 160072 (2016).
15. Veraart J, Novikov DS, Christiaens D, et al. Denoising of Diffusion MRI using random matrix theory. Neuroimage 2016; 142:394-406.
16. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs‐ringing artifact removal based on local subvoxel‐shifts. Magn Reson Med 2016; 76: 1574–1581
17. Rokem A, Yeatman JD, Pestilli F, et al. Evaluating the accuracy of diffusion MRI models in white matter. PLoS One 2015: 10; e0123272.
18. Sotiropoulos SN, Jbabdi S, Xu J, et al. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage 2013: 80; 125–143.
Figures