3761
RIESLING: Radial Interstices Enable Speedy Low-volume Imaging1Neuroimaging, King's College London, London, United Kingdom, 2ASL Europe, GE Healthcare, Munich, Germany
Synopsis
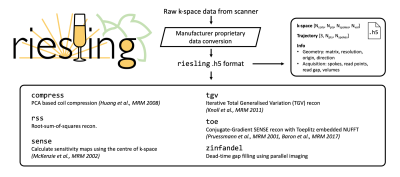
We present an image reconstruction toolbox tuned for 3D radial ZTE images named Radial Interstices Enable Speedy Low-volume imagING (RIESLING). RIESLING matches the image quality of existing toolboxes while enabling fast reconstructions of high resolution ZTE datasets.
Introduction
For many years Cartesian k-space acquisition has been the dominant paradigm for MR Imaging. Recently various forms of non-cartesian imaging have become more popular. One such method is zero echo time (ZTE)1,2 pulse sequences which have several unique advantages over conventional MR acquisitions, for instance the ability to visualise bone and its near silent acoustic properties3,4. The natural k-space acquisition scheme for volumetric ZTE imaging is 3D center-out radial. This presents distinct challenges for efficient reconstruction compared to 2D non-cartesian schemes, particularly when parallel imaging is considered. Hence, although several open-source recon toolboxes support both 2D and 3D non-cartesian imaging5,6,7, we developed a reconstruction toolbox specifically tailored towards 3D radial imaging, which we name Radial Interstices Enable Speedy Low-volume ImagiNG (RIESLING).Methods
Outline of SoftwareRIESLING is implemented in C++, utilising multi-threaded versions of both the Eigen tensor library8 and the FFTW library9. A simple HDF5 (.h5) file format was adopted which includes the k-space data, trajectory, and metadata such as matrix size and resolution. The methods implemented in RIESLING are listed in Figure 1. Following the gold-standard cgSENSE framework10, the key algorithmic steps are density compensation, interpolation (gridding), channel combination, and optionally regularisation. Here we describe how we tuned each step to best suit 3D radial imaging.
In 2D iterative reconstruction, density compensation is often omitted as it does not strongly affect convergence. In contrast, for 3D imaging, a very large number of non-cartesian points overlap in the centre of k-space and correct density compensation is therefore essential to stabilize convergence. While it is straightforward to obtain an analytic density compensation (~1/r2), this is only valid in the fully sampled case. Pipe & Menon showed that in 2D, once an acquisition is undersampled, analytic compensation leads to noise inflation by over-weighting the edges of k-space14. The correct weighting in the under-sampled regions is a constant. We empirically determined that for 3D radial the transition occurs at kmax/√R, where R is the acceleration rate, and provide both analytic weights and Pipe & Menon's iterative weight-finding scheme.
Interpolation is generally accomplished by convolution with a Kaiser-Bessel kernel and subsequent de-apodization11,12. In 3D, this convolution is expensive, as a 3x3x3 kernel requires 27 memory writes per non-cartesian point. Oesterle et al. showed that in 2D, the kernel can be omitted, provided that the cartesian grid is at least 2x oversampled13. ZTE sequences typically utilise 2x acquisition oversampling to increase the FoV to avoid folding artefacts from protons in the coil housing, and hence a 2x reconstruction grid is a natural fit. To parallelize the gridding, we build a list of non-cartesian index/cartesian coordinate pairs and then sort by the cartesian coordinates. The resulting list is trivially parallelized, and the cost of sorting is minimal.
The critical step in parallel imaging is the combination of multiple channel images. It has long been known that radial and spiral trajectories are suitable for self-calibration as they possess a fully sampled central region of k-space15. We exploit this property in RIESLING to produce sensitivity maps by gridding the central region of k-space with a modified density compensation16.
Previous work has demonstrated the power of regularisation for improving the image quality of undersampled images. We provide an implementation of the Total Generalised Variation (TGV) method, which has been shown to provide superior results to Total Variation (TV) for radial imaging17.
Modern multi-channel coils lead to large memory requirements. A typical 1 mm isotropic voxel size brain image with 32-channels reconstructed on a 2x oversampled grid requires 22Gb of memory at 32-bit float precision. To reduce the data size, we apply Principal Component Analysis coil-compression before reconstruction18.
Evaluation
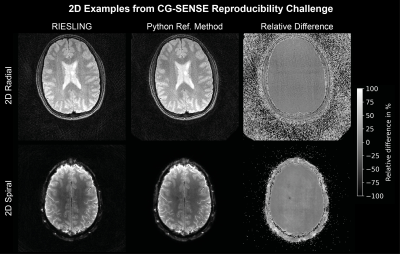
We compared RIESLING to the ISMRM cgSENSE reproducibility challenge data19, which contains 2D radial and spiral datasets. We also show results from a 3D radial ZTE sequence implemented on a 3T scanner (GE MR 750) equipped with a 32-channel (Nova Medical) head coil. One dataset is a volunteer scanned with an IR-prepared sequence (1 mm isotropic voxels, 220 mm isotropic FoV, 15.6 kHz bandwidth, TI 450 ms, FA 2°). The second is a half bottle of Riesling Eiswein (Johannisberg 2018, The Wine Society) scanned with a PD-weighted sequence (2 mm isotropic voxels, 220 mm isotropic FoV, 41.67 kHz bandwidth, FA 1°).
Results
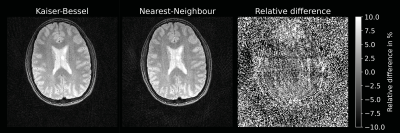
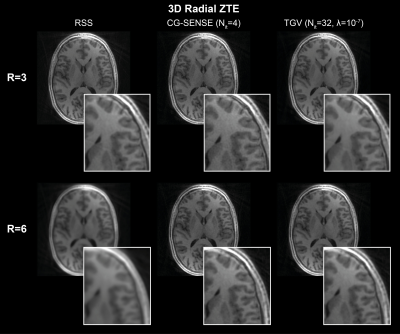
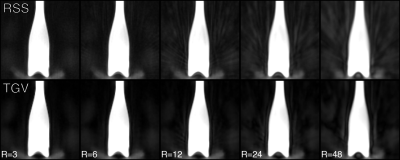
Figure 2 compares nearest-neighbour gridding to the kaiser-bessel method in the 2D dataset, showing negligible difference in image quality. All other images use nearest-neighbour gridding. Reconstruction of the 2D cgSENSE challenge dataset using RIESLING produced results strikingly similar to the Python reference method, as shown in Figure 3.The different reconstruction methods in RIESLING are demonstrated in Figure 4 using the 3D radial dataset. RIESLING is multi-threaded for fast performance even on a CPU - reconstructing these images on a 6-core Mac Mini took 15 seconds per iteration, for a total reconstruction time of 8 minutes. Finally, Figure 5 shows the bottle of Riesling scanned with progressively higher angular under-sampling, demonstrating the robustness of the 3D ZTE sequence against streaking artefacts.
Conclusion
RIESLING is an efficient reconstruction framework for 2D and 3D non-cartesian data. The code is open source and available on github at: github.com/spinicist/riesling.Acknowledgements
This work was supported by the Wellcome/EPSRC Centre for Medical Engineering [WT 203148/Z/16/Z] and the NIHR Clinical Research Facility at King's College Hospital.
References
[1] D. P. Madio and I. J. Lowe, “Ultra-Fast Imaging Using Low Flip Angles and FIDs,” Magn. Reson. Med., vol. 34, no. 4, pp. 525–529, 1995.
[2] M. Weiger and K. P. Pruessmann, “MRI with Zero Echo Time,” eMagRes, vol. 1, pp. 311–322, 2012.
[3] F. Wiesinger et al., “Zero TE MR bone imaging in the head,” Magn. Reson. Med., vol. 75, no. 1, pp. 107–114, 2016.
[4] S. Alibek et al., “Acoustic noise reduction in MRI using Silent Scan: An initial experience,” Diagnostic Interv. Radiol., vol. 20, no. 4, pp. 360–363, 2014.
[5] J. Tamir, F. Ong, J. Y. Cheng, M. Uecker, and M. Lustig, “Generalized Magnetic Resonance Image Reconstruction using The Berkeley Advanced Reconstruction Toolbox,” in ISMRM Workshop on Data Sampling and Image Reconstruction, 2016.
[6] F. Ong and M. Lustig, “SigPy: A Python Package for High Performance Iterative Reconstruction,” in Proc. Intl. Soc. Mag. Reson. Med. 27, 2019, p. 4819.
[7] M. S. Hansen and T. S. Sørensen, “Gadgetron: An open source framework for medical image reconstruction,” Magn. Reson. Med., vol. 69, no. 6, pp. 1768–1776, 2013.
[8] G. Guennebaud, B. Jacob, P. Avery, A. Bachrach, and S. Barthelemy, “Eigen v3.” 2010.
[9] M. Frigo and S. G. Johnson, “The Design and Implementation of FFTW3,” Proc. IEEE, vol. 93, no. 2, pp. 216–231, 2005.
[10] K. P. Pruessmann, M. Weiger, P. Börnert, and P. Boesiger, “Advances in Sensitivity Encoding With Arbitrary k-Space Trajectories,” Magn. Reson. Med., vol. 46, no. 4, pp. 638–651, 2001.
[11] J. A. Fessler, “On NUFFT-based gridding for non-Cartesian MRI,” J. Magn. Reson., vol. 188, no. 2, pp. 191–195, 2007.
[12] J. I. Jackson, C. H. Meyer, D. G. Nishimura, and A. Macovski, “Selection of a Convolution Function for Fourier Inversion Using Gridding,” IEEE Trans. Med. Imaging, vol. 10, no. 3, pp. 473–478, 1991.
[13] C. Oesterle, M. Markl, R. Strecker, F. M. Kraemer, and J. Hennig, “Spiral reconstruction by regridding to a large rectilinear matrix: A practical solution for routine systems,” J. Magn. Reson. Imaging, vol. 10, no. 1, pp. 84–92, 1999.
[14] J. G. Pipe and P. Menon, “Sampling density compensation in MRI: Rationale and an iterative numerical solution,” Magn. Reson. Med., vol. 41, no. 1, pp. 179–186, 1999.
[15] E. N. Yeh et al., “Inherently self-calibrating non-cartesian parallel imaging,” Magn. Reson. Med., vol. 54, no. 1, pp. 1–8, 2005.
[16] C. A. Baron, N. Dwork, J. M. Pauly, and D. G. Nishimura, “Rapid compressed sensing reconstruction of 3D non-Cartesian MRI,” Magn. Reson. Med., vol. 00, no. August, 2017.
[17] F. Knoll, K. Bredies, T. Pock, and R. Stollberger, “Second order total generalized variation (TGV) for MRI,” Magn. Reson. Med., vol. 65, no. 2, pp. 480–491, 2011.
[18] F. Huang, S. Vijayakumar, Y. Li, S. Hertel, and G. R. Duensing, “A software channel compression technique for faster reconstruction with many channels,” Magn. Reson. Imaging, vol. 26, no. 1, pp. 133–141, 2008.
[19] O. Maier et al., “CG-SENSE revisited: Results from the first ISMRM reproducibility challenge,” Magn. Reson. Med., no. October, pp. 1–19, 2020.
Figures