3757
Using GrOpt with Pulseq for Easy Prototyping of Pulse Sequences with Optimized Waveforms1Radiology, Stanford University, Stanford, CA, United States, 2Radiology, Veterans Affairs Health Care System, Palo Alto, CA, United States, 3Computer Science, Technical University of Munich, Garching, Germany, 4Cardiovascular Institute, Stanford University, Stanford, CA, United States
Synopsis
The objective of this work was to demonstrate the integration of two open-source MRI software packages: GrOpt and Pulseq. GrOpt allows for robust and fast optimization of gradient waveforms subject to various constraints, while Pulseq allows a flexible and straightforward approach to writing sequences and executing them on a scanner. We demonstrate example pulse sequences that integrate both software packages and show an imaging example from a PC-MRI experiment. The combination of GrOpt and Pulseq allows for optimized arbitrary gradient waveforms to be easily prototyped and run on a scanner.
Introduction
Gradient waveform design for MRI pulse sequences has traditionally been accomplished with an ad hoc combination of analytical methods based primarily on combining gradient waveforms into trapezoid-like shapes. These methods have proven to work well; however, a growing body of research has shown they can be improved upon with numerical optimization techniques1-10.By treating gradient waveform design as a numerical optimization problem, one can use constraints to define pulse sequence requirements (e.g. gradient moments) and hardware limitations (gradient and slewrate maxima). This allows for the design of time-optimal gradient waveforms, making the sequence more efficient. It also affords the opportunity to reduce artifacts (e.g. reduce eddy current induced artifacts) or better mitigate physiological constraints (e.g. reduce peripheral nerve stimulation, PNS).
Recently, an open-source, vendor-agnostic software package that provides a flexible framework for gradient optimization (GrOpt) has been described11. GrOpt allows for a wide range of waveforms to be designed, with very little compute time required (usually on the order of milliseconds). GrOpt enables both simple and complex gradient waveform designs to be easily solved on the scanner, but the arbitrarily shaped gradient waveforms can be difficult to implement within a specific vendor’s pulse sequence environment.
Pulseq is a software package12 that allows for fast prototyping of sequences on scanners by using a simple Matlab toolbox to generate sequence files, which can be executed directly on a scanner through a custom sequence that reads and executes GrOpt’s resultant Matlab gradient waveforms. The objective of this work was to demonstrate and provide code examples for the integration of GrOpt and Pulseq, allowing optimized gradient waveforms to be easily integrated on a scanner in a straightforward manner.
Methods
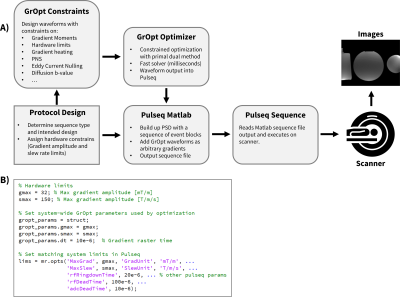
An overview of the workflow is presented in Figure 1A. First, system configuration and hardware design values are entered into Pulseq as well as GrOpt, so that waveforms remain consistent (Fig. 1B).GrOpt is written in C and includes Matlab (and Python) wrappers that enable direct integration with Pulseq. The Matlab implementation of Pulseq was used to generate the final sequences, which supports adding arbitrary gradient waveform blocks from GrOpt into the sequence timing. Gradient areas and timings can be easily exchanged between the two packages, allowing GrOpt to be used throughout the design process in combination with Pulseq designed components. The output of the Pulseq software is a sequence file that is copied onto a scanner and executed by the Pulseq protocol.
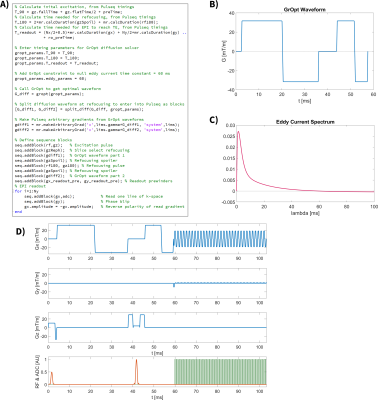
Demonstrations include several implemented examples of GrOpt optimized sequences in Pulseq. The first is an eddy current nulled EPI diffusion sequence (EN-CODE), as previously published10. This involves integrating the diffusion encoded gradient waveforms from GrOpt into a default Pulseq EPI sequence. The diffusion waveform is designed to maximize b-value, while nulling a given eddy current time constant (60ms) to mitigate distortion.
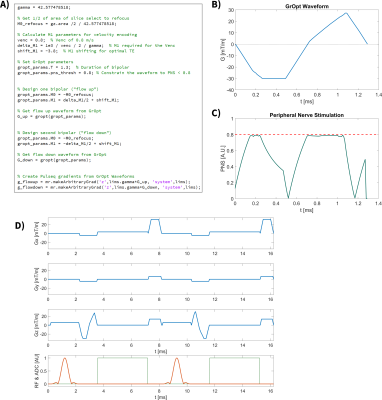
The second example presented is a peripheral nerve stimulation (PNS) constrained phase contrast MRI (PC-MRI) sequence6. This sequence adds two flow encoding bipolar gradients into a Pulseq SPGR sequence. The bipolars include a VENC (M1) constraint of 80 cm/s, and the sequence places a point-wise constraint on PNS, while using the full gradient amplitude and slew rate whenever possible. This allows for faster waveforms as compared to the standard method of globally derating the slew rate to accommodate PNS.
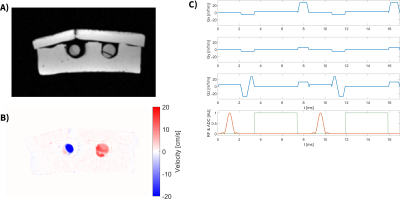
A GrOpt+Pulseq PC-MRI sequence using conventional, time-optimal bipolars was scanned on a 3.0T scanner (Siemens Skyra) using a flow phantom setup with known flow rate13. Images were reconstructed offline and investigated for artifacts and flow quantification.
All the code used to generate the sequences, and the sequence files themselves, are available at github.com/mloecher/gropt_pulseq.
Results
Figure 2 highlights the EN-CODE diffusion sequence, which shows the code required to add the optimized waveforms, the resultant GrOpt waveforms, and their eddy current response, as well as a portion of the full Pulseq sequence. Figure 3 shows a similar overview for the PNS constrained PC-MRI waveforms. Figure 4 shows images from the PC-MRI experiment. The measured flow rates from the Pulseq PC-MRI sequence were in excellent agreement with the programmed flow rate (62.8 mL/s Pulseq vs. 60.0 mL/s programmed). Compute times for all GrOpt portions of the waveform generation were <1 second, and the total waveform generation time was ~5 seconds for both examples to run Pulseq builds and checks.Discussion
In this work we demonstrated the use of Pulseq to more easily prototype optimized gradient waveforms generated by GrOpt. Sequences can be coded entirely in Matlab, with flexible options for a range of sequences. One of the limitations of this methodology is that sequences are only created for a very specific set of parameters and changing any parameter on the scanner UI requires re-generating the sequence files in Matlab. However, this could be advantageous for quality control protocols in multi-site/multi-vendor studies. A wide range of optimized waveforms can be tested with this framework, allowing for easier development and testing of new MR sequences. The methodology also allows for common acquisitions and reconstructions to be conducted on cross-vendor studies (Pulseq can currently run on Siemens and GE clinical scanners)14.Acknowledgements
R01 HL131823 and R01 HL152256 to DBEReferences
[1] O. P. Simonetti, J. L. Duerk, and V. Chankong, “MRI gradient waveform design by numerical optimization.,” Magnetic Resonance in Medicine, vol. 29, pp. 498–504, apr 1993.
[2] B. A. Hargreaves, D. G. Nishimura, and S. M. Conolly, “Time-optimal multidimensional gradient waveform design for rapid imaging,” Magnetic Resonance in Medicine, vol. 51,pp. 81–92, jan 2004.
[3] J. A. Derbyshire, D. A. Herzka, E. R. McVeigh, and R. J. Lederman, “Efficient implementation of hardware-optimized gradient sequences for real-time imaging.,” Magnetic Resonance in Medicine, vol. 64, pp. 1814–1820, Dec. 2010. [4] B. D. Bolster and E. Atalar, “Minimizing dead-periods in flow-encoded or -compensated pulse sequences while imaging in oblique planes.,” Journal of magnetic resonance imaging : JMRI, vol. 10, pp. 183–192, Aug. 1999.
[5] M. J. Middione, H. H. Wu, and D. B. Ennis, “Convex gradient optimization for increased spatiotemporal resolution and improved accuracy in phase contrast MRI,” Magnetic Resonance in Medicine, vol. 72, no. 6, pp. 1552–1564, 2014.
[6] M. Loecher, P. Magrath, E. Aliotta, and D. B. Ennis, “Time-optimized 4D phase contrast MRI with real-time convex optimization of gradient waveforms and fast excitation methods,” Magnetic Resonance in Medicine, vol. 82, no. 1, pp. 213–224, 2019.
[7] J. Sjölund, F. Szczepankiewicz, M. Nilsson, D. Topgaard, C.-F. Westin, and H. Knutsson,“Constrained optimization of gradient waveforms for generalized diffusion encoding,” Journal of Magnetic Resonance, vol. 261, pp. 157–168, 2015.
[8] Szczepankiewicz, Filip, et al. "Motion‐compensated gradient waveforms for tensor‐valued diffusion encoding by constrained numerical optimization." Magnetic Resonance in Medicine (2020).
[9] Yang, Grant, and Jennifer A. McNab. "Eddy current nulled constrained optimization of isotropic diffusion encoding gradient waveforms." Magnetic resonance in medicine 81.3 (2019): 1818-1832.
[10] Aliotta, Eric, Kévin Moulin, and Daniel B. Ennis. "Eddy current–nulled convex optimized diffusion encoding (EN‐CODE) for distortion‐free diffusion tensor imaging with short echo times." Magnetic resonance in medicine 79.2 (2018): 663-672.
[11] Loecher, Michael, Matthew J. Middione, and Daniel B. Ennis. "A gradient optimization toolbox for general purpose time‐optimal MRI gradient waveform design." Magnetic Resonance in Medicine 84.6 (2020): 3234-3245.
[12] Layton, Kelvin J., et al. "Pulseq: a rapid and hardware‐independent pulse sequence prototyping framework." Magnetic resonance in medicine 77.4 (2017): 1544-1552.
[13] Zimmermann J, Loecher M, Bäumler K, Cork TE, Gifford K, Marsden A, Fleischmann D, Ennis DB. In Vitro 4D-Flow and Pressure Mapping in the True and False Lumen of a Type-B Aortic Dissection Model. SCMR 24th Annual Meeting, San Diego, California (Virtual), 2021.
[14] Nielsen, Jon‐Fredrik, and Douglas C. Noll. "TOPPE: A framework for rapid prototyping of MR pulse sequences." Magnetic resonance in medicine 79.6 (2018): 3128-3134.
Figures