3741
Assessment of Uncertainty in Brain MRI Deformable Registration1Applied Mathematics, Technion, Haifa, Israel, 2Biomedical Engineering, Technion, Haifa, Israel
Synopsis
Unsupervised deep neural networks (DNN) are successfully employed to predict deformation-fields in neuroimaging studies. Bayesian DNN models enable safer utilization of DNN methods in neuroimaging studies, improve generalization and enable assessment of uncertainty in the predictions. We propose a non-parametric Bayesian approach to estimate the uncertainty in DNN-based algorithms for brain MRI deformable registration. We demonstrated the added-value of our Bayesian registration framework on the brain MRI (LPBA40) dataset compared to state-of-the-art VoxelMorph DNN. Further, we quantified the uncertainty of the registration and assessed its correlation with the out-of-distribution data.
Introduction
Deep neural networks (DNN) are currently used in wide range of computer vision and image processing tasks. Specifically, these methods play a key role in MRI analysis and reconstruction, in which they provide efficient solutions to challenging tasks such as MRI reconstruction from under-sampled data [1], and image registration [2,3], to name a few. However, the practical utilization of DNN in neuroimaging applications is hampered by the lack of computational mechanisms for quantifying the risks of failures in the DNN predictions, which is necessary to derive clinical and scientific conclusions in neuroimaging. Bayesian DNN models can enable a safer utilization of DNN methods in neuroimaging, improve generalization and assess the uncertainty of the predictions [4].Methods
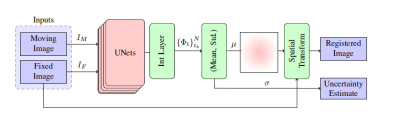
We treat the brain MRI registration DNN weights as random variables and aim to sample the posterior distribution of the model prediction. We efficiently sample the actual posterior distribution of the model weights using a SGLD mechanism [5]. To this end, we incorporate a noise scheduler that injects a time-dependent Gaussian noise to the gradients of the loss during the optimization process.Fig.1 illustrates the design of our Bayesian registration DNN framework. Our main building-block is a UNet-based CNN similar to the VoxelMorph model [2]. Given a pair of moving and target images as a 2-channel input, it predicts the deformation field. Sampling from the UNet outputs is analogous to having a set of stochastic UNets characterized by different weights; each operates on the same pair of moving and fixed images and models the corresponding deformation field. The operation of the system at the inference stage is as follows: it takes a pair of moving and target images and predicts the posterior deformation field by computing the average of the deformation field predictions obtained by the stochastic UNets. Lastly, it maps each pixel in the moving image by applying the spatial transform function.
Results and Discussion
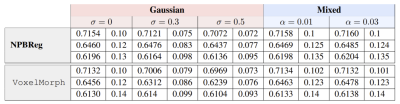
We used the LPBA40 database [6]. The LPBA40 database consists of brain MRI scans of 40 subjects with provided segmentation into 56 structures within the cortex. We assessed the performance of our Bayesian unsupervised DNN registration system by means of Dice score. We compared the registration result of our method and the baseline VoxelMorph [2]. We assessed the robustness of our approach against noisy images by corrupting the input images with two types of noise: Gaussian noise with various std and mixed structures [7], which generated a linear combination of the test example (i) and another example sampled randomly from the test set (j). Our Bayesian methods shows an improvement over VoxelMorph in noisy scenarios (Table 1, p-value<0.01). In addition, we assessed the ability of our uncertainty measures to predict out-of-distribution data. We produced out of distribution data by injecting Gaussian noise with different standard deviation to the input images. Then we computed the uncertainty maps of the deformation field. Our uncertainty scores were highly correlated with out-of-distribution data (Fig. 2, r>0.95, p<0.01).Conclusions
Incorporating Bayesian approaches in DNN-based systems has a significant impact on practical utilization in neuroimaging applications. The Bayesian methods provide principled mechanisms to quantify the risks of failures in the DNN predictions, which is necessary in the safety-critical neuroimaging applications. Our Bayesian DNN-based model improves generalization, allows the assessment of the uncertainty in the predictions and provides a principled mechanism to determine out-of-distribution data.Acknowledgements
Freiman, M. is a Taub fellow (supported by the Taub Family Foundation).References
[1] Shaul, Roy, et al. "Subsampled Brain MRI Reconstruction by Generative Adversarial Neural Networks." Medical Image Analysis (2020): 101747.
[2] Balakrishnan, Guha, et al. "An unsupervised learning model for deformable medical image registration." Proceedings of the IEEE conference on computer vision and pattern recognition. 2018.
[3] Yang, Xiao, et al. "Quicksilver: Fast predictive image registration–a deep learning approach." NeuroImage 158 (2017): 378-396.
[4] Neal, Radford M. Bayesian learning for neural networks. Vol. 118. Springer Science & Business Media, 2012.
[5] Welling, Max, and Yee W. Teh. "Bayesian learning via stochastic gradient Langevin dynamics." Proceedings of the 28th international conference on machine learning (ICML-11). 2011.
[6] Shattuck, David W., et al. "Construction of a 3D probabilistic atlas of human cortical structures." Neuroimage 39.3 (2008): 1064-1080.
[7] Freiman, Moti, Ravindra Manjeshwar, and Liran Goshen. "Unsupervised abnormality detection through mixed structure regularization (MSR) in deep sparse autoencoders." Medical physics 46.5 (2019): 2223-2231.
Figures