3653
Toward high-resolution mapping of microscopic anisotropy in the cortex using b-tensor diffusion imaging with a spiral readout at 7 Tesla1Department of Neurology and Neurosurgery, McGill University, Montreal, QC, Canada, 2McConnell Brain Imaging Center, Montreal Neurological Institute, McGill University, Montreal, QC, Canada, 3Department of Biomedical Engineering, McGill University, Montreal, QC, Canada
Synopsis
High-resolution diffusion-weighted imaging has been used to investigate the microstructure of the cortex in vivo. However, conventional linear diffusion encoding provides limited insight into the underlying microstructural differences between cortical areas. b-Tensor encoding disentangles macroscopic from microscopic anisotropy in voxels with complex fiber geometries. The SNR and thus resolution of these scans are limited by the longer diffusion encoding times. A DWI sequence with b-tensor encoding was implemented at 7T with a spiral readout trajectory and dynamic field monitoring to image cortical microstructure. Microscopic anisotropy maps of the brain are presented at 1.4 mm isotropic, within minimal distortions and blurring.
Introduction
Various MRI contrasts such as relaxometry and magnetisation transfer (MT) have been employed to map the microstructure and composition of the cerebral white and gray matter 1,2. Diffusion-weighted imaging (DWI) techniques offer complementary information about the tissue microstructure 3. However, conventional linear diffusion-encoding schemes show limitations in estimating microstructural features that are independent from the complex macroscopic fiber geometry in a voxel. b-Tensor encoding has shown promising results by encoding diffusion along a multi-dimensional trajectory in q-space instead of a single linear direction 4,5. b-Tensor encoding can be used to estimate microscopic anisotropy (µFA), which reflects the mean of the true microscopic anisotropy of the microenvironments in a voxel. This capability makes b-tensor DWI a suitable candidate for probing the complex microstructure of the cortex 6. However, this technique has a low signal-to-noise ratio (SNR) due to long diffusion-encoding times, which limits the achievable resolution. To increase the spatial resolution to investigate the cortex, we implemented the sequence at 7 Tesla (T) with a spiral readout to minimize signal loss due to T2 decay.Methods
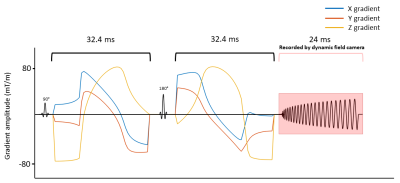
MR scanning was performed on a 7T Terra (Siemens, Erlangen, Germany) using a 32-channel receive coil on one human subject. Spherical and planar tensor encoding (STE and PTE) gradient waveforms were optimized using the Euclidian norm, a maximum gradient amplitude and slew rate of 80 mT/m and 100 T/m/s respectively, a heating coefficient of 0.9, and 100 temporal samples using Numerical Optimization of gradient Waveforms (NOW) 7. The duration of the waveforms before and after the refocusing pulse was 32.4 ms. Stejskal-tanner pulses were used for linear tensor encoding (LTE) with the same duration as the STE and PTE waveforms. We used the protocol described in Szczepankiewicz et al. 8, with diffusion-encoding strengths b = [100, 700, 1400, 2000] s/mm2. For spherical encoding, 10 rotations for each b-value were performed, and two repetitions were acquired. Linear and planar encoding were performed for 10, 10, 16, and 46 rotations for the same b-values, respectively.A spiral trajectory was designed using the Hargreaves algorithm 9 to minimize the duration for a maximum gradient amplitude of 35 mT/m and slew rate of 125 T/m/s. This resulted in a 24-ms readout for an in-plane resolution of 1.4×1.4 mm2, a field of view of 250×250 mm2, and a 4 times undersampled trajectory.
Diffusion scans were acquired with TE = 78 ms, TR = 4200 ms, and 3 slices of 1.4 mm thickness (Figure 1). A gradient-echo (GRE) sequence with 6 echos, TE1 = 3.13 ms, ΔTE = 1.15 ms, TR = 600 ms, slice thickness of 1.4 mm, and in-plane resolution of 1×1 mm2 was acquired for the same slices for coil sensitivity estimation and ΔB0 mapping. Total acquisition time was 22 minutes. All scans were monitored using a dynamic field camera (Skope MRT, Zurich, Switzerland) in a separate session.
The images were reconstructed using an in-house MATLAB script based on the expanded signal model, incorporating effects of static field nonuniformities as well as readout trajectory imperfections up to the 3rd order of spherical harmonics 10. This required inverting the eddy current compensation performed by the scanner. Coil sensitivity maps were obtained by reconstructing individual images of the first GRE echo for each coil, combining them as in Walsh et al. 11, and then using MatMRI toolbox 12. ΔB0 maps were estimated by temporal unwrapping of phase images from the multi-echo GRE acquisition, and then refined by smoothing using a variational method 13. The diffusion images were denoised 14, corrected for motion 15, and analysed using the multi-dimensional diffusion MRI (MD-dMRI) framework 15. The data were fitted to a covariance model to map mean diffusivity (MD), FA, and µFA.
Results and discussion
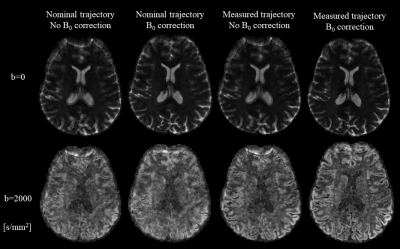
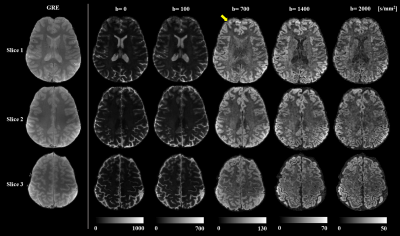
Image reconstruction was performed accounting for trajectory imperfections and static field nonuniformities. Figure 2 shows their impact on the reconstructed image quality of one slice and two different contrasts. Artifacts are more pronounced for high b-values due to eddy currents caused by the diffusion encoding gradients, which affect the fidelity of the readout trajectory.Reconstructed diffusion images in Figure 3 show fine details of the cortex in all contrasts with minimal blurring, a common artifact caused by spiral readouts. In comparison to the GRE images, the diffusion images show minimal distortions, which is crucial for investigation of the cortex. The shorter echo time achieved using a spiral readout resulted in a gain in SNR 16 that enabled us to acquire scans with considerably smaller voxel sizes (1.4 mm isotopic) in comparison to common b-tensor protocols with a 2-3 mm2 in-plane resolution and a 2-4 mm slice thickness 17–19.
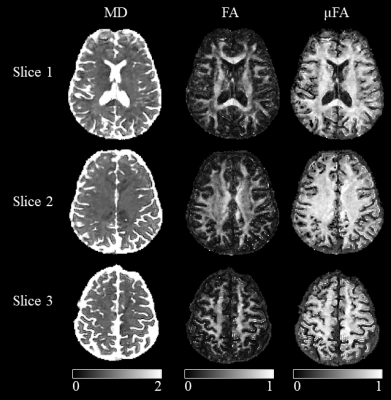
Mean diffusivity (MD), FA and µFA maps of 3 slices are shown in Figure 4. Similarly to previous works 20, the µFA of the cortex is much higher than FA, and the contrast within the white matter is much lower as well.
Conclusion
This study presents a b-tensor diffusion encoding sequence implemented at 7T with a spiral readout and dynamic field monitoring in order to achieve high-resolution images with minimal distortions, which is crucial for accurate alignment in multi-parametric studies. Further resolution improvements can be achieved by employing high-SNR readout strategies, such as 3-D trajectories.Acknowledgements
The authors would like to thank Dr. Cameron Cushing and Dr. Paul Weavers (Skope MR Inc, WI, USA), and Dr. Christian Mirkes (Skope Magnetic Resonance Technologies AG, Zurich) for their technical support and feedback on this work. Also, we would like to thank Dr. Marcus Couch (Siemens Collaboration Scientist) for his technical support, and Mr. Ronaldo Lopez (McConnell Brain Imaging Center) for helping with the human scan.
This project was funded by the Natural Sciences and Engineering Research Council of Canada, the Fonds de recherche du Québec – Santé, and Healthy Brains for Healthy Lives. The data was acquired at the McConnell Brain Imaging Centre, which is supported by the Canadian Foundation for Innovation, Brain Canada, and Healthy Brains for Health Lives.
References
1. Does, M. D. Inferring Brain Tissue Composition and Microstructure via MR Relaxometry. Neuroimage 182, 136–148 (2018).
2. Nürnberger, L. et al. Longitudinal changes of cortical microstructure in Parkinson’s disease assessed with T1 relaxometry. NeuroImage: Clinical 13, 405–414 (2017).
3. Stikov, N. et al. In vivo histology of the myelin g-ratio with magnetic resonance imaging. Neuroimage 118, 397–405 (2015).
4. Westin, C.-F. et al. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage 135, 345–362 (2016).
5. Nilsson, M. et al. Tensor‐valued diffusion MRI in under 3 minutes: an initial survey of microscopic anisotropy and tissue heterogeneity in intracranial tumors. Magn Reson Med 83, 608–620 (2020).
6. Lampinen, Z. et. al. Tensor-valued diffusion MRI differentiates cortex and white matter in malformations of cortical development associated with epilepsy. Epilepsia 61, 1701–1713 (2020).
7. Sjölund, J. et al. Constrained optimization of gradient waveforms for generalized diffusion encoding. J Magn Reson 261, 157–168 (2015).
8. Szczepankiewicz, F., Hoge, S. & Westin, C.-F. Linear, planar and spherical tensor-valued diffusion MRI data by free waveform encoding in healthy brain, water, oil and liquid crystals. Data in Brief 25, 104208 (2019).
9. Lee, J. H., Hargreaves, B. A., Hu, B. S. & Nishimura, D. G. Fast 3D imaging using variable-density spiral trajectories with applications to limb perfusion. Magn Reson Med 50, 1276–1285 (2003).
10. Wilm, B. J., Barmet, C., Pavan, M. & Pruessmann, K. P. Higher order reconstruction for MRI in the presence of spatiotemporal field perturbations. Magnetic Resonance in Medicine 65, 1690–1701 (2011).
11. Walsh, D. O., Gmitro, A. F. & Marcellin, M. W. Adaptive reconstruction of phased array MR imagery. Magn Reson Med 43, 682–690 (2000).
12. Baron, C. A., Dwork, N., Pauly, J. M. & Nishimura, D. G. Rapid Compressed Sensing Reconstruction of 3D Non-Cartesian MRI. Magn Reson Med 79, 2685–2692 (2018).
13. Lourakis, M. TV-L1 Image Denoising Algorithm. (2020).
14. Veraart, J., Fieremans, E. & Novikov, D. S. Diffusion MRI noise mapping using random matrix theory. Magn Reson Med 76, 1582–1593 (2016).
15. Nilsson, M. et al. An open-source framework for analysis of multidimensional diffusion MRI data implemented in MATLAB. (2018).
16. Lee, Y. et al. On the signal-to-noise ratio benefit of spiral acquisition in diffusion MRI. Magn Reson Med (2020) doi:10.1002/mrm.28554.
17. Lampinen, B. et al. Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: A model comparison using spherical tensor encoding. NeuroImage 147, 517–531 (2017).
18. Szczepankiewicz, F., Sjölund, J., Ståhlberg, F., Lätt, J. & Nilsson, M. Tensor-valued diffusion encoding for diffusional variance decomposition (DIVIDE): Technical feasibility in clinical MRI systems. PLOS ONE 14, e0214238 (2019).
19. Arezza, N. J. J., Tse, D. H. Y. & Baron, C. A. Rapid Microscopic Fractional Anisotropy Imaging via an Optimized Kurtosis Formulation. medRxiv 2020.11.23.20237099 (2020) doi:10.1101/2020.11.23.20237099.
20. Lawrenz, M., Brassen, S. & Finsterbusch, J. Microscopic diffusion anisotropy in the human brain: reproducibility, normal values, and comparison with the fractional anisotropy. Neuroimage 109, 283–297 (2015).
Figures