3635
Optimization of B0 Simulation Strategy in the Human Heart based on CT Images at limited Field of View1Department of Biomedical Engineering, Columbia University, New York, NY, United States, 2Chair of Cellular and Molecular Imaging, Comprehensive Heart Failure Center, University Hospital Wuerzburg, Wuerzburg, Germany, 3Department of Cardiovascular Imaging, Comprehensive Heart Failure Center, University Hospital Wuerzburg, Wuerzburg, Germany, 4Department of Radiology, Columbia University Medical Center, New York, NY, United States
Synopsis
B0 simulation in the heart based on thoracic CT images is a powerful tool to investigate cardiac B0 conditions in the general population for the development of an optimized cardiac B0 shimming strategy. Thoracic CT scans typically have a limited field of view posing a challenge to the accuracy of field simulations. Here we present a systematic analysis of errors introduced by B0 computations in the human heart from CT-based susceptibility distributions of limited field of view and present strategies to resemble B0 conditions in the human heart to achieve elevated accuracy with model-based addition of selected anatomical features.
Introduction
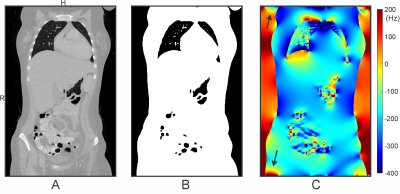
Human cardiac MRI adopting balanced steady-state free precession (SSFP) sequences suffers from dark band artifacts1 due to B0 inhomogeneity2,3. The best remedy for mitigating this issue is to homogenize B0 distribution in the heart through B0 shimming4. The development of an optimized cardiac B0 shimming strategy in the general population necessitates understanding B0 conditions encountered in the human heart. We recently presented proof-of-principle for efficiently obtaining cardiac B0 maps by field simulation based on susceptibility distributions derived from readily available whole-thoracic CT images5. However, thoracic CT scans typically have a limited Field of View (FOV) that does not include the entire body's susceptibility information, causing a challenge to field simulation accuracy due to 1) boundary effects potentially stretching across the entire FOV when using rapid FFT-based numerical methods6-8 and 2) lack of relevant anatomical structures contributing to B0 conditions in the heart such as head, shoulders, arms, and legs (Figure 1). Here, we present a systematic analysis of errors induced by B0 simulation in the heart from CT-based susceptibility distributions of limited FOV and strategies to achieve elevated accuracy with model-based addition of selected anatomical features.Methods
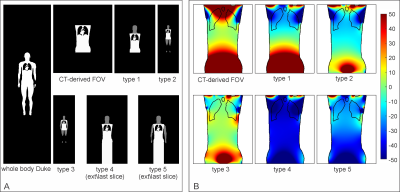
The fidelity of B0 field simulations in the human heart was analyzed employing two numerical models, "Duke" and "Ella"9 (Virtual Population V2.0 models, IT'IS Foundation, Zurich, Switzerland). A gold standard was established by computing B0 distributions as the superposition of dipole fields10 for the entire body, i.e., from head to toe. B0 simulations utilizing the FFT-based method and under specific conditions, e.g., limited FOV, were then compared to this gold standard. The simulation error was characterized as the standard deviation (STD) of field differences between the two methods in the heart. The effects induced by the discretization of susceptibility distributions and boundary effects of finite computation volume8 were investigated individually by calculating B0 maps at different spatial resolutions (2 mm through 9 mm isotropic) and zero-padding factors (1.5 to 6.0) to find the best possible accuracy while maintaining a matrix size that can be handled computationally (Dell Poweredge T440, CPU: Intel Xeon 4116, RAM: 64 GB). Field calculations were performed for 3 T using B0DETOX11 software.To mitigate the effects on B0 distribution in the heart caused by lack of anatomical structures, we investigated adopting anatomical parts from another generic body. Model Duke was cut to the FOV of a typical thoracic CT scan and extended from model Ella by adopting head, including shoulder (type 1), legs (type 2) and arms (type 3) step by step. Replacing the legs by repeating the last body slice instead of zero-filling was further investigated for types 2 and 3 to reduce matrix size, leading to types 4 and 5 (Figure 3A). The performance of these extension approaches in FFT-based field simulations were evaluated by analyzing the B0 field differences compared to the simulation using Duke's entire body.
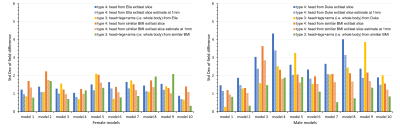
We further tested the performance of types 3 (all anatomical parts) and 4 (minimum matrix size) by applying them to 10 male and 10 female human models12 with various BMIs. We investigated the strategies 1) adopting parts from Duke to male models and Ella to female models and 2) extending models from another body with similar BMI by field comparison to each model’s entire body at 2.5 mm isotropic. The simulation error of type 4 at the highest achievable resolution (1 mm isotropic) was estimated by scaling the STD by a factor extrapolated from the simulation data.
Results
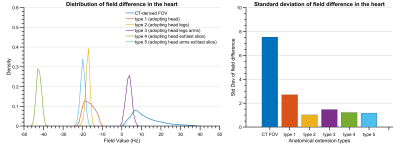
The standard deviation of the field differences between the FFT-based and dipole method decreased with improved zero-padding factor then converged at a factor between 2 and 3, beyond which spatial resolution has a more prominent effect on the simulation accuracy (Figure 2). The higher spatial resolution led to more accurate results with smaller STD values for all zero-padding factors. Therefore, we chose a zero-padding factor of 2.5 and the highest possible spatial resolution of 2 mm isotropic within the computation capability.All anatomical extension approaches showed substantially less B0 simulation errors than the original CT–type FOV with more homogeneous field differences and lower STD values (Figure 3B and 4). The anatomical extension type 3 adopting the body with a similar BMI exhibited the lowest B0 simulation error with an average STD of 1.2 Hz across female models and 1.1 Hz in male models (Figure 5). The STD values of type 4 at 1 mm resolution with similar BMI, scaled by a factor of 0.78, was more comparable to type 3. Type 4 was a suitable compromise to achieve high-resolution B0 simulation with less discretization error under limited computation power.
Discussion
Here we present an analysis of the impact of spatial resolution, zero-padding factor, and anatomical extension on cardiac B0 simulation accuracy at 3 T. We disentangled and quantified error sources associated with cardiac B0 distributions when computed from magnetic susceptibility distributions of limited FOV. We demonstrated that high B0 fidelity can be achieved with the model-based extension of human anatomy on a regular PC. The derived simulation approach will be used to compute cardiac B0 maps from a large set of CT images for the development of a population-based cardiac B0 shimming strategy.Acknowledgements
No acknowledgement found.References
1. Ferreira PF, Gatehouse PD, Mohiaddin RH, Firmin DN. Cardiovascular magnetic resonance artefacts. J Cardiovasc Magn Reson. 2013;15(1):41.
2. Atalay MK, Poncelet BP, Kantor HL, Brady TJ, Weisskoff RM. Cardiac susceptibility artifacts arising from the heart‐lung interface. Magn Reson Med. 2001;45(2):341-345.
3. Schär M, Kozerke S, Fischer SE, Boesiger P. Cardiac SSFP imaging at 3 Tesla. Magn Reson Med. 2004;51(4):799-806.
4. Juchem C, de Graaf RA. B0 magnetic field homogeneity and shimming for in vivo magnetic resonance spectroscopy. Analytical Biochemistry. 2017;529:17-29.
5. Shang Y, Theilenberg S, Mattar W, Terekhov M, Jambawalikar SR, Schreiber L, Juchem C. High Resolution Simulation of B0 Field Conditions in the Human Heart Based on Segmented CT Images. Proc Int Soc Magn Reson Med 2019;2184.
6. Marques J, Bowtell R. Application of a Fourier‐based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concepts Magn Reson. 2005;25B(1):65-78.
7. Salomir R, de Senneville BD, Moonen CT. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concepts Magn Reson. 2003;19B(1):26-34.
8. Koch KM, Papademetris X, Rothman DL, de Graaf RA. Rapid calculations of susceptibility-induced magnetostatic field perturbations for in vivo magnetic resonance. Phys Med Biol. 2006;51(24):6381-6402.
9. Gosselin MC, Neufeld E, Moser H, Huber E, Farcito S, Gerber L, Jedensjo M, Hilber I, Di Gennaro F, Lloyd B, Cherubini E, Szczerba D, Kainz W, Kuster N. Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0. Phys Med Biol. 2014;59(18):5287-5303.
10. Muller-Bierl B, Graf H, Steidle G, Schick F. Compensation of magnetic field distortions from paramagnetic instruments by added diamagnetic material: measurements and numerical simulations. Med Phys. 2005;32(1):76-84.
11. Juchem C. B0DETOX - B0 Detoxification Software for Magnetic Field Shimming. Columbia TechVenture (CTV), License CU17326 2017;innovation.columbia.edu/technologies/cu17326_b0detox
12. Segars WP, Sturgeon G, Mendonca S, Grimes J, Tsui BM. 4D XCAT phantom for multimodality imaging research. Med Phys. 2010;37(9):4902-4915.
Figures