3607
Three-dimensional cardiac T1 mapping using subspace and sparsity constrained direct estimation1Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States, 2LTCI, Telecom Paris, Institut Polytechnique de Paris, Paris, France
Synopsis
Cardiac T1 mapping is a powerful MR imaging technique for quantitative assessment of microstructural changes in myocardial tissues. Existing methods are limited in terms of spatial coverage and through-plane resolution due to limitations in acquisition speed and the presence of cardiac and respiratory motion. This work presents a direct reconstruction framework, which allows estimation of 3D T1 maps from sparsely sampled k-space data using physical modeling through the Bloch equation, low-rank constraints on the dynamic images and sparsity constraints on the estimated T1 maps.
Introduction
Cardiac T1 mapping provides quantitative assessment of microstructural changes in myocardial tissues and is widely used for detection of cardiomyopathies and evaluation of myocardial structure[1]. Cardiac T1 mapping is challenging due to physiological motion. Methods have been proposed for 3D T1 mapping of the heart utilizing accelerated imaging with ECG-gated acquisitions over single[2]/multiple breath-holds[3] or using respiratory bellows or navigators [4–6]. Recently, low-rank based approaches have been proposed to resolve respiratory and cardiac motion by exploiting correlations in a high-dimensional subspace. This enables T1 mapping with non-ECG-gated acquisitions [7–9]. However, these works involve estimation of T1 as a separate process subsequently after image reconstruction, and do not fully utilize the physical model of signal dynamics related to T1 recovery during image reconstruction. Direct parametric mapping has been proposed for 2D cardiac T1 mapping and has shown improved results over indirect estimation [10]. We propose a direct estimation framework for free-breathing 3D cardiac T1 mapping, which allows estimation of T1 maps from sparsely sampled k-space data using physical modeling through the Bloch equation, low-rank constraints on the dynamic images and sparsity constraints on the estimated T1 maps. We validate performance of the proposed method using in-vivo data acquired on a 3T MR scanner.Methods
T1 maps are reconstructed using a combination of subspace-based image reconstruction and fitting to a physical model of the signal governed by the Bloch equation. The proposed method solves the optimization problem stated in Fig. 1. The constrained optimization problem consists of data fidelity and a pair of regularization terms, solved for finding the spatial bases denoted by $$$U_s$$$ and parametric maps $$$\theta$$$ (including T1 and transmit B1). The spatio-temporal distribution of the signal is modeled by a set of spatial bases $$$U_s$$$ and temporal bases $$$V_t$$$. Two regularizers are used: one penalizing the spatial-spectral sparsity of the MR signal and the other penalizing the total variation (TV) in the estimated T1 map. The function $$$f$$$ maps the estimated parameters to the spatio-temporal MR images through solutions of the Bloch equation. The optimization problem is solved using ADMM [12] which results in the sequence of updates listed in Fig. 1. The first step (Eq. (2)) updates $$$U_s$$$ using a low-rank constrained reconstruction with a $$$\ell_1$$$ sparsity penalty. The second step (Eq. (3)) consists of a penalized fitting problem to update parametric images. A second ADMM is performed to decouple the TV and fitting terms and therefore allow a pixel-wise fitting operation. This pixel-wise fitting problem is solved using a grid search on the nonlinear parameters (T1 and transmit B1) of the signal model. To eliminate the effect of motion, fitting is performed on individual motion phases. The second subproblem of this nested ADMM is a TV denoising problem which can be efficiently solved.Results
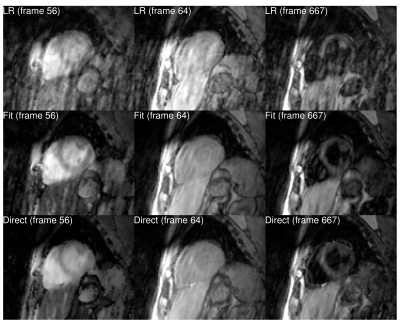
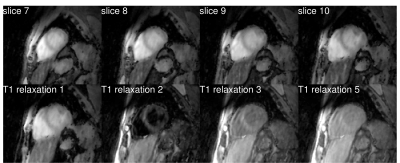
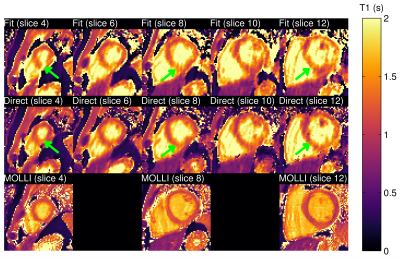
One healthy subject was scanned on a 3T Siemens Trio scanner (Siemens Healthcare, Erlangen, Germany) using an inversion recovery sequence following a 5-(3)-5-(3) protocol: non-selective inversion pulses were applied every 8 cardiac cycles with different delay times of 100 and 180 ms; k-space data were acquired at the end of diastole in 5 cardiac cycles and no data acquisitions were performed in the following 3 cardiac cycles to allow for T1 recovery. The k-space data was acquired using variable density sampling on a Cartesian grid, each frame containing 68 k-space lines, including 12 training lines for estimation of the temporal bases [13]. The matrix size was 384x162x16 with resolution of 2.8x2.8x8 mm$$$^3$$$. Other acquisition parameters were: TR = 3 ms, TE = 1.5 ms, flip angle = 6°. The total acquisition time was 20 minutes. A separate acquisition with 2D MOLLI [14] was performed for comparison. A comparison of images obtained using low-rank reconstruction without physical model (LR), synthesized images obtained after applying simple fit on images from low-rank reconstructions (Fit), and images obtained with the proposed direct estimation method (Direct) is shown in Fig. 2. Images from low-rank reconstruction exhibited aliasing artifacts which degraded image quality. Synthesized images showed reduction of these artifacts. The proposed direct estimation approach further improved the image quality with suppression of aliasing artifacts. This was also confirmed in images for different slices and T1 recovery time (Fig. 3). Estimated T1 maps from the indirect estimation (i.e., from synthesized images) and the proposed direct estimation method are shown for several slices in Fig. 4. As indicated by the green arrows, indirect estimation resulted in apparent nonuniformity of the T1 values within the myocardium. The proposed direct reconstruction method showed improvement in T1 estimation better matching with those from MOLLI in terms of myocardial shape and thickness.Conclusion
We present a direct estimation framework for free-breathing 3D cardiac T1 mapping. The method allows estimation of 3D T1 maps from sparsely sampled k-space data using physical modeling through the Bloch equation, low-rank constraints on the dynamic images and sparsity constraints on the estimated T1 maps. The performance of the proposed method is validated in-vivo.Acknowledgements
This work was supported in part by the National Institutes of Health under awardnumbers: T32EB013180, R01CA165221, R01HL118261, R21MH121812,R01HL137230, K01EB030045, and P41EB022544.References
[1] Messroghli DR, Moon JC, Ferreira VM, Grosse-Wortmann L, He T, Kellman P, et al. Clinical recommendations for cardiovascular magnetic resonance mapping of T1, T2, T2* and extracellular volume: A consensus statement by the Society for Cardiovascular Magnetic Resonance (SCMR) endorsed by the European Association for Cardiovascular Imaging (EACVI). Journal of Cardiovascular Magnetic Resonance 2017;19:75.
[2] Chen Y, Lo W-C, Hamilton JI, Barkauskas K, Saybasili H, Wright KL, et al. Single breath-hold 3D cardiac T1 mapping using through-time spiral GRAPPA. NMR in Biomedicine 2018;31:e3923.
[3] Wang S-C, Patel AR, Tanaka A, Wang H, Ota T, Lang RM, et al. A novel profile/view ordering with a non-convex star shutter for high-resolution 3D volumetric T1 mapping under multiple breath-holds. Magnetic Resonance in Medicine 2017;77:2215–24.
[4] Weingartner S, Akcakaya M, Roujol S, Basha T, Stehning C, Kissinger KV, et al. Free-breathing post-contrast three-dimensional T1 mapping: Volumetric assessment of myocardial T1 values. Magnetic Resonance in Medicine 2015;73:214–22.
[5] Guo R, Chen Z, Wang Y, Herzka DA, Luo J, Ding H. Three-dimensional free breathing whole heart cardiovascular magnetic resonance T1 mapping at 3 T. Journal of Cardiovascular Magnetic Resonance 2018;20:64.
[6] Nordio G, Bustin A, Henningsson M, Rashid I, Chiribiri A, Ismail T, et al. 3D SASHA myocardial T1 mapping with high accuracy and improved precision. Magma 2019;32:281–9.
[7] Qi H, Jaubert O, Bustin A, Cruz G, Chen H, Botnar R, et al. Free-running 3D whole heart myocardial T1 mapping with isotropic spatial resolution. Magnetic Resonance in Medicine 2019;82:1331–42.
[8] Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie Y, Wang N, et al. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nature Biomedical Engineering 2018;2:215–26.
[9] Shaw JL, Yang Q, Zhou Z, Deng Z, Nguyen C, Li D, et al. Free-breathing, non-ECG, continuous myocardial T1 mapping with cardiovascular magnetic resonance multitasking. Magnetic Resonance in Medicine 2019;81:2450–63.
[10] Wang X, Kohler F, Unterberg-Buchwald C, Lotz J, Frahm J, Uecker M. Model-based myocardial T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH cardiovascular magnetic resonance 2019.
[11] Liang Z-P. Spatiotemporal Imaging with Partially Separable Functions. IEEE International Symposium on Biomedical Imaging, 2007, p. 988–91.
[12] Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends in Machine Learning 2011;3:1–22
[13] Han PK, Horng DE, Marin T, Petibon Y, Ouyang J, El Fakhri G, Ma C. Free-Breathing Three-Dimensional T1 Mapping of the Heart Using Subspace-Based Data Acquisition and Image Reconstruction. IEEE Engineering in Medicine and Biology Society Conference, 2019, p. 4008–4011
[14] Kellman P, Wilson JR, Xue H, Ugander M, Arai AE. Extracellular volume fraction mapping in the myocardium, part 1: Evaluation of an automated method. Journal of Cardiovascular Magnetic Resonance 2012;14:63.
Figures