Introduction

Quantitative cardiac T1 mapping is of increasing interest in clinical cardiovascular magnetic resonance (CMR) imaging [1,2]. Recent developments on free-breathing T1 mapping [3,4] have enabled high-resolution T1 mapping at multiple cardiac phases without breathhold, overcoming the limitations of the conventional breathhold techniques such as MOLLI [5] and SASHA [6]. These methods usually extract motion (respiration and/or cardiac) signals from a non-Cartesian sampled k-space center using self-gating, followed by a motion-resolved image reconstruction and pixel-wise fitting. Meanwhile, model-based reconstructions have been developed for cardiac T1 mapping [7-9]. The latter directly estimates myocardial parameter maps from k-space enabling very high acceleration. In this work, we combine these strategies using a motion-resolved model-based reconstruction for free-breathing T1 mapping with a free-running inversion-recovery radial FLASH sequence. Validations of the proposed method have been performed on an experimental phantom and two healthy subjects.

Theory and Methods

Sequence Design and Motion Estimation

The free-breathing T1 mapping sequence is shown in Fig 1. It consists of 1) a non-selective inversion 2) continuous radial FLASH readout with a tiny golden-angle ~$$$23.63^\circ$$$ 3) and a time gap (5 second) between inversions to ensure recovery of the longitudinal magnetization. The above process was repeated 20 times, resulting a total acquisition time of around 3 minutes. After data acquisition, an adapted SSA-FARY technique [10] was applied on the k‐space center of all radial spokes and all coils to extract the signal component that is most relevant for respiratory motion. Cardiac motion synchronization was accomplished with the signal recorded using an external ECG device.

Motion-Resolved Model-Based Reconstruction

The acquired k-space data is sorted into 6 respiration and 17 cardiac phases. To estimate parameter maps from all phases, a previously developed model-based reconstruction [8,9] is extended: the estimation of parameter maps and coil sensitivity maps from all states is formulated as a nonlinear inverse problem:
$$\begin{equation}\begin{split}\hat{x} &= \text{argmin}_{x} \|\sum_{i=1}^{N_{{R}}}\sum_{j=1}^{N_{{C}}}F_{i,j}(x) -\widetilde{Y}_{i,j} \|_{2}^{2} + \alpha R(x_{{p}}) + \beta U(x_{{c}}) \\&s.t. \quad x \in D\end{split}\end{equation}$$
with $$$F$$$ a nonlinear operator [8] mapping all unknowns $$$x$$$ to the sorted $$$k$$$-space data $$$\widetilde{Y}$$$. $$$N_{{R}}$$$, $$$N_{{C}}$$$ are the numbers of respiration, cardiac phases respectively. $$$x_{{p}}$$$ contains steady-state signal $$$M_{ss}$$$, equilibrium signal $$$M_{0}$$$ and effective relaxation rate $$$R_{1}^{*}$$$ of each motion state, $$$x_{{c}}$$$ is the set of corresponding coil sensitivity maps. $$$R(\cdot)$$$ is the regularization on the parameter maps:$$\begin{equation}R(x_{{p}}) = \|Wx_{{p}}\|_1 + \|x_{p}^{R}\|_{\text{TV}} + \|x_{p}^{C}\|_{\text{TV}}\end{equation}$$ with $$$\|Wx_{{p}}\|_1$$$ the joint $$$\ell_{1}$$$-Wavelet spatial regularization, $$$\|x_{p}^{R}\|_{\text{TV}}$$$ and $$$\|x_{p}^{C}\|_{\text{TV}}$$$ the temporal total variation (TV) regularization [11] along the respiration and cardiac dimensions, respectively. $$$U({\cdot})$$$ represents the Sobolev norm enforcing the smoothness of coil sensitivity maps. $$$\alpha$$$ and $$$\beta$$$ are the regularization parameters for parameter and coil sensitivity maps, respectively. $$$D$$$ is a convex set ensuring $$${R^{*}_{1}}$$$ to be nonnegative.
Similar to [8,9], the above nonlinear inverse problem is solved by the IRGNM algorithm. To enable multiple regularizations, the ADMM algorithm [12] is employed to solve the linearized subproblem in each Gauss-Newton step.

Data Acquisition

All MRI experiments were performed on a Magnetom Skyra 3T (Siemens Healthineers, Erlangen, Germany). Combined thorax and spine coils with 26 channels were utilized for all scans. Phantom measurements were performed with simulated respiration and cardiac signals (respiration cycle: 3 second, heart rate: 60 bpm). The other acquisition parameters were: FOV: $$$256 \times 256$$$ mm$$$^{2}$$$, matrix size: $$$192 \times 192$$$, slice thickness 6 mm, TR/TE = 3.27/1.98 ms, bandwidth 810 Hz/pixel. All in-vivo measurements were acquired using the nominal flip angle $$$6^{\circ}$$$ and repeated twice. All data processing was done offline and implemented in BART [13].

Results

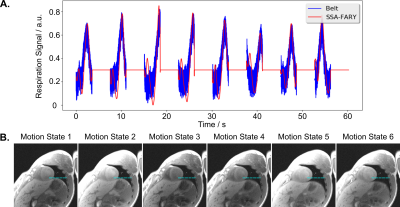
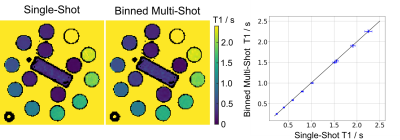
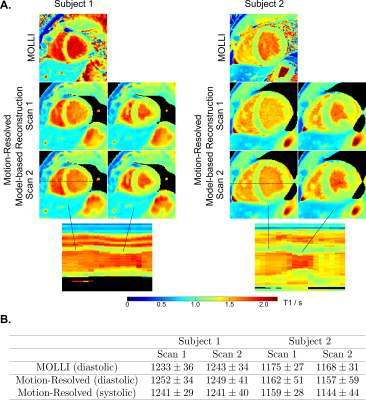
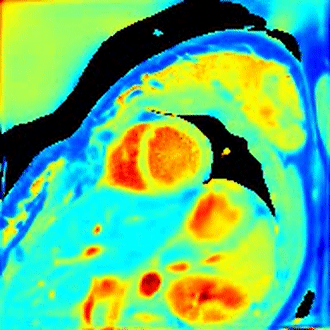
Fig 2A shows an extracted respiration signal against the respiration belt signal. The corresponding bin images of 6 respiratory motion states are presented in Fig 2B. The clearly motion-resolved motion images suggest that the adapted SSA-FARY technique could resolve respiratory motion. Fig 3 compares single-shot phantom T1 map [9] and the multi-shot T1 map estimated by motion-resolved model-based reconstruction. Visual inspection reveals good agreement between these two T1 maps. This finding is further confirmed by the quantitative ROI-analysed T1 values shown in Fig 3 (right). Fig 4A depicts MOLLI T1 map (mid-diastolic) and two representative motion-resolved T1 maps (mid-diastolic and mid-systolic) for two repetitive scans and two subjects. The line profiles along the motion dimension are shown in the bottom. The small visual difference between the repetitive scans demonstrates good intra-subject reproducibility of the proposed method, which is again confirmed by the quantitative results in Fig 4B. Additionally, myocardial T1 values of the proposed method are also in a similar range as MOLLI. Note the lateral area of the T1 map from the second subject is slightly blurred which may due to an inaccurate cardiac motion estimation. Finally, Fig 5 presents a dynamic T1 mapping example at the end-expiration state for subject 1.

Discussion and Conclusion

This work develops a free-breathing myocardial T1 mapping technique using a free-running inversion-recovery radial FLASH sequence and a motion-resolved model-based reconstruction. Initial results on an experimental phantom and two healthy subjects have demonstrated good accuracy, precision and reproducibility of the proposed method. However, the present work is limited in the number of subjects and imperfect motion estimation. Further investigation and more clinical validations of the proposed method will be explored in future studies.

Acknowledgements

Supported by the DZHK (German Centre for Cardiovascular Research).