3591

Constrained UNFOLD (CoUNFOLD)-a New Constrained Reconstruction for Hyperpolarized 13C Pyruvate Imaging

Zhan Xu¹, Christopher M Walker¹, Collin J Harlan¹, Keith A Michel¹, Gary V Martinez¹, and James A Bankson^1,2
¹Imaging Physics, MD Anderson Cancer Center, Houston, TX, United States, ²UT Health Graduate School of Biomedical Sciences, The University of Texas MD Anderson Cancer, Houston, TX, United States

Synopsis

A new pharmacokinetic-model-based constrained reconstruction method CoUNFOLD is introduced for hyperpolarized 13C pyruvate imaging. This method extended classic UNFOLD method by introducing model constraint which described the signal evolution of multiple substrates. CoUNFOLD successfully accelerated the data acquisition, and the reconstruction was implemented on single channel. An in silico experiment demonstrated the accuracy of reconstruction at a reduction factor of 2. The quantitative estimation of the conversion ratio from pyruvate to lactate was achieved with high accuracy when peak pyruvate SNR was as low as 20

Purpose

Hyperpolarized (HP) MRI using [1-¹³C]-pyruvate has been demonstrated as a non-invasive approach to monitor dynamic metabolic exchange in cancer imaging with tremendous sensitivity and specificity^1.The apparent conversion rate of HP 13C pyruvate to lactate (k_pl) reflects aerobic glycolysis (the Warburg effect) and has been shown as an important imaging biomarker for staging cancer and assessing response to therapy. However, HP MRI is challenging because magnetization is finite, nonstationary, and nonrenewable. Because the downstream metabolites of pyruvate is SNR-limited, HP dynamic imaging is usually acquired at an expense of low spatial or temporal resolution. Data reduction strategies can be used to improve resolution and reduce the burden of spatiotemporal encoding. Here we propose and investigate a new model-based constrained reconstruction algorithm, Constrained UNFOLD (CoUNFOLD), to enhance image resolution from an undersampled broadband echo-planar imaging sequence² with alternating spectral-spatial excitation of key metabolites.

Theory:

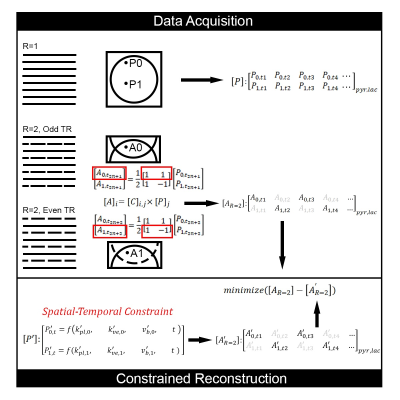
CoUNFOLD implements imaging acceleration in the same way as UNFOLD³, by reducing the FOV at each acquisition, as presented in Figure 1. The acceleration ratio R is defined as 1 for a full resolution acquisition and reflects the ratio of fully sampled to undersampled data in accelerated acquisition. When an object is undersampled at R=2, only half the data points in k-space are acquired at the odd (or even) phase encoding steps. In a dynamic acquisition, alternating subsets of data can be acquired at each repetition. Correspondingly, each alised voxel point (such as A₀ or A₁) in the half FOV aliased image is the superposition of two points (P₀ and P₁) from the original fully encoded FOV image. The relationship between A_m and P_n is demonstrated by the linear equation $$$A_{m}=C_{m,n}\times P_{n}$$$ , where $$$C_{m,n}=\frac{1}{R} exp^{-2\pi j\cdot m\cdot n}$$$ , $$$m,n=1,...,R$$$.
The time varying spatial undersampling scheme encodes some of the spatial information (k) into the temporal domain (t), and standard UNFOLD resolves the aliasing via distinct temporal modulation on P₀ and P₁ in the same image. Unlike UNFOLD, CoUNFOLD reconstruction is based on the pharmacokinetic model, which defines the dynamic evolution of multiple substrates from different images. As a result, the unaliasing of A₀ (or A₁) is achieved concurrently with the estimation of model parameters that in turn predicts full FOV images.

Method

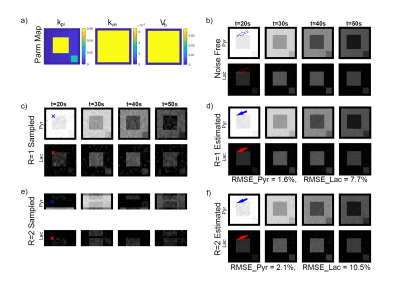
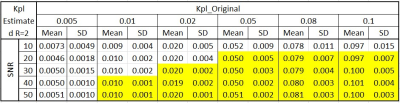
A digital reference object (DRO) with predefined pharmacokinetic model parameters was used to synthesize full FOV images, which can be seen in Figure 2a and 2b. The model accounts for two chemical pools (HP pyruvate and lactate), and two well-mixed physical compartments (vascular and extravascular) ⁴. The dynamic metabolite curves at each voxel are defined by three primary parameters: k_pl, the apparent conversion rate for HP pyruvate into lactate; k_ve, the extravasation rate; and v_b, the extracellular volume fraction. All other nuisance parameters, including T1_Pyr and T1_Lac, were designated as constants over all locations. The flip angle was set to 20 degrees for both pyruvate and lactate over all 60 repetitions (TR=2s). The k_plmap is designed to simulate a FOV (matrix size 16-by-16) with regions at different kpl rates. Gaussian white noise was added to simulate a full resolution acquisition (Figure 2c) with a maximum pyruvate SNR of 30. The noisy images were then fit to estimate the primary parameters and noise-free, fully encoded images (Figure 2d).
Two voxels sampled at R=2 were repeated 100 times under various SNRs to test the accuracy for quantitative estimation of k_pl. The target voxel was synthesized at various k_pl values, while the background voxel was set at k_pl=0.1, The k_ve, v_b, and all other parameters were identical for both voxels.

Result

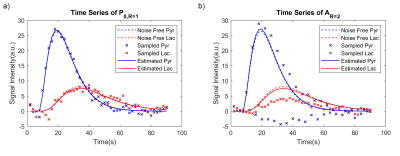
When R=2, the aliased image series presented a dark/bright alternative pattern as a result of summation (odd TRs) / subtraction (even TRs) of two voxels (P₀ and P₁) that were $$$\frac{FOV}{2}$$$ away from each other (Figure 2e). This is also reflected by the drastically fluctuated time series of a randomly selected voxel located in the upper half of the FOV (blue ‘x’ in Figure 3b). These images were used as an input to CoUNFOLD, which successfully reconstructed unaliased images with high accuracy. The fractional RMSE of reconstructed pyruvate images over all spatial locations was merely 2.1% with respect to noise-free images. The fractional RMSE of lactate images was 10.5%, due in part to the low SNR of lactate signal.

The quantitative estimation of k_pl presented a high accuracy under certain limitations, as shown in table 1. Both high k_pl and high SNR improved the accuracy. When k_pl was as low as 0.01 the minimal SNR to reach reliable k_pl estimation (mean and SD < 10%, as highlighted in Table 1) was 40, while a lower peak SNR of 20 was needed for a k_pl of 0.1 to achieve the same performance.

Discussion & Conclusion

CoUNFOLD is a promising image reconstruction approach for accelerated HP [1-¹³C] pyruvate imaging with high accuracy. It also presented the potential to be a quantitative approach under sufficient SNR and metabolic conditions. Future work will test the reconstruction performance at higher undersampling ratio and its reliability in retrospective and prospective phantom and human studies.

Acknowledgements

This work was supported in part by the National Cancer Institute of the National Institutes of Health (R01CA211150). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.

References

[1] Golman, K., et al. (2006) Metabolic imaging by hyperpolarized 13C magnetic resonance imaging for in vivo tumor diagnosis. Cancer research 66, 10855-10860

[2] Gordon, J.W., et al. (2017) Development of a symmetric echo planar imaging framework for clinical translation of rapid dynamic hyperpolarized (13) C imaging. Magn. Reson. Med., 77, 826-832

[3] Madore, B., et al. (1999) Unaliasing by fourier-encoding the overlaps using the temporal dimension (UNFOLD), applied to cardiac imaging and fMRI. Magn. Reson. Med., 42, 813-828

[4] Bankson, J.A., et al. (2015) Kinetic Modeling and Constrained Reconstruction of Hyperpolarized [1-13C]-Pyruvate Offers Improved Metabolic Imaging of Tumors. Cancer research 75, 4708-4717

Figures

Data acquisition and constrained reconstruction scheme of CoUNFOLD. P stands for a pixel in the full FOV image, A stands for an aliased pixel in the undersampled (R stands for the ratio) image with reduced FOV, A’ is the estimated aliased pixel that is calculated under the same undersampling scheme as A from the CoUNFOLD reconstructed image. The solid and dashed lines represent, respectively, the acquired and skipped phase steps in k-space.

Representative acquired and reconstructed images from full resolution images (R=1) and undersampled images (R=2). (a) Maps of primary parameters of the digital reference object. (b) Noise-free pyruvate and lactate images from four time points. (c, d) Full resolution images sampled at SNR=30, and the estimated images from them using the pharmacokinetic model. (e, f) Undersampled images at SNR=30, and the CoUNFOLD reconstructed images from them. The arrows and crosses indicate voxels at the same location from different image modalities, whose time series are shown in Figure 3.

The time series at the same voxel location from different undersampling rates. (a) The sampled metabolite series ('x') at SNR=30 are fluctuating along the noise free series (dash lines), while the estimated series (solid) from pharmacokinetic model matches the noise free series with slight offset. (b) The undersampled pyruvate series (blue 'x') at SNR=30 fluctuate drastically around the noise-free series(dashed lines) and the lactate series(red 'x') are severely deviated, but the CoUNFOLD restored series (solid) match the noise free series only with moderate offset.

Estimation accuracy of kpl from CoUNFOLD reconstructed images of undersampled images at R=2. Estimation root mean square error RMSE and standard deviation (SD) is over 100 runs. The reliable estimation, defined as whose RMSE and SD both have less than 10% from the actual kpl, are highlighted.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

3591