3587
A genetic algorithm-optimized hetero-nuclear polarization transfer pulse sequence for metabolic imaging1Cancer Research UK Cambridge Institute, University of Cambridge, Li Ka Shing Centre, Robinson Way, Cambridge, United Kingdom, 2Department of Radiology, University of Cambridge, School of Clinical Medicine Box 218, Cambridge Biomedical Campus, Cambridge, United Kingdom, 3Department of Information Technology and Electrical Engineering, ETH Zurich, Rämistrasse 101, Zurich, Switzerland, 4Department of Biochemistry, University of Cambridge, Tennis Court Road, Cambridge, United Kingdom
Synopsis
An optimized polarization transfer pulse designed using a genetic algorithm is presented, which has greater immunity to the effects of B0 and B1 field inhomogeneity and ~2 times lower peak B1 compared to the BINEPT pulse sequence. The optimization provides a simple framework that accounts for finite pulse lengths and relaxation and outputs a shaped pulse on each frequency channel. Performance was tested on a [15N2]urea phantom at thermal equilibrium, where the polarization transferred from protons to 15N was 1.32 times greater than that transferred using BINEPT. Partial transfer of polarization from hyperpolarized 15N to proton was also demonstrated.
Introduction
Pulse sequence design can be challenging due to both an involved theoretical description and experimental imperfections, which can reduce the efficiency of a pulse sequence. For example, in a typical polarisation transfer sequence such as INEPT (insensitive nuclei enhanced by polarization transfer), which has been used recently for metabolic imaging with hyperpolarized [1-13C]pyruvate1,2, hardware constraints can reduce the increased sensitivity imparted by proton detection of the hyperpolarized X-nucleus1,3. These polarization transfer sequences have employed adiabatic pulses, however a compromise has to be made between frequency selectivity and their robustness to B1 inhomogeneity. Polarization transfer efficiency can also be reduced with longer adiabatic pulses, which is particularly severe when there is strong J-coupling and the polarization transfer element of the sequence is consequently much shorter. Relaxation losses, driven by higher numbers of strongly coupled spins and longer transfer times, result in decreased sensitivity4. The high energy deposition and peak B1 amplitude of adiabatic pulses is also a problem for clinical applications. As a potential solution to this problem, we investigated pulse sequence optimization using a genetic algorithm. A genetic algorithm is a stochastic solver working with a "population" of solutions and discovering subspaces of the overall search space at every iteration according to probabilistic lower bounds. Therefore, convergence to a global optimum is possible with no initial guess and convexity requirements on the cost function5. A further advantage over the gradient based approaches such as optimal control6,7 is that a cost function gradient does not need to be calculated, therefore constraints are easy to incorporate and including time-steps among optimization variables does not imply additional complexity. We demonstrate the feasibility of this approach with full transfer of 1H to 15N polarization in a [15N2]urea phantom (J = 90 Hz) at thermal equilibrium, where the performance of the optimized pulse sequence was compared with the BINEPT8 seqeunce (B1-insensitive nuclear enhancement through polarization transfer) and in a partial transfer of 15N polarization to 1H in a hyperpolarized [15N2]urea phantom3.Methods
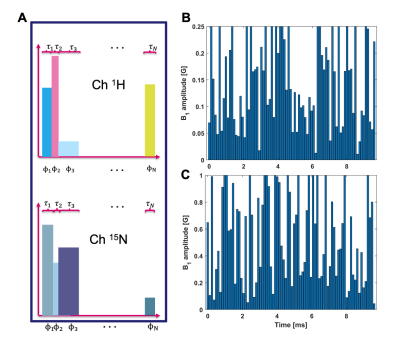
The optimization treats the pulse sequence as a shaped pulse on each frequency channel. The pulses are discretized to N number of time-steps. Each pulse point has an amplitude, duration and phase, giving rise to three degrees of freedom per RF channel (see Figure 1). The only restriction is the number of time-steps, which gives an upper bound for the number of RF pulses. The amplitude of the RF pulses can be constrained to match the performance of the transmit coil. Relaxation is estimated by means of an uncorrelated random fields model. Spin dynamics simulations are performed in the cost function. The value of the cost function is obtained by comparing the final density operator, which is the result after the transfer block, to the preferred density operator. The preferred density operator is user specified and reflects the desired result, e.g. all magnetization is on the proton x-axis. The cost function is evaluated over a range of frequency offsets and B1 amplitudes to yield robust transfer. The spin dynamics were simulated with in-house Matlab (The Mathworks, Natick, Massachusetts) scripts. The transfer values were validated using SpinDynamica (www.spindynami ca.soton.ac.uk) in Wolfram Mathematica (version 11; Wolfram Research, Inc, Champaign, Illinois) and showed good agreement. Experiments were performed using a 7T MRI scanner (Agilent, Palo Alto, CA) with a home-built dual-tuned 1H-15N transmit-receive surface coil, which allowed simultaneous pulsing on both frequency channels.Results
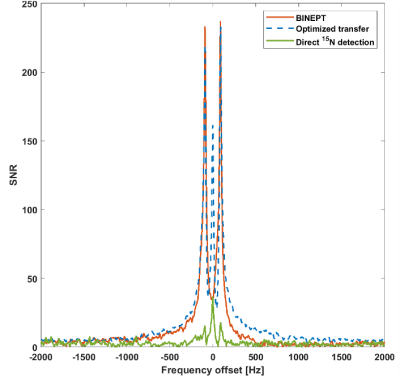
Polarization transfer from proton to 15N in an [15N2]urea phantomPolarization is transferred from the two magnetically equivalent protons to the 15N nucleus. The integral of the 15N triplet with the proposed method was 1.32 and 9.79 times higher when compared to that obtained using BINEPT and direct 15N detection respectively. The optimized sequence better preserved the multiplet structure, which is believed to be lost due to anti-phase magnetization resulting from the long adiabatic pulses (Figure 2). The proposed method also required more than 2 times lower peak B1 compared to the BINEPT pulse sequence.
Partial polarization transfer from 15N to proton in a hyperpolarized [15N2]urea phantom
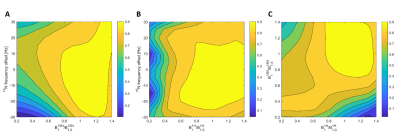
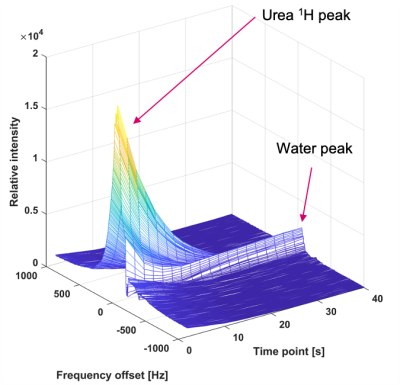
Polarization is transferred from the hyperpolarized 15N nucleus to the protons in discrete packets to demonstrate the feasibility of dynamic experiments. The importance of such an experiment is discussed in the paper describing the IRRUPT sequence3, a partial transfer version of BINEPT. Simulations showed ΔB0 and B1 robustness comparable to IRRUPT (Figure 3.). The signal was observable for up to 24 s (12 repetitions) even though the injection of the hyperpolarized solution to the Eppendorf-tube significantly degraded the shim and therefore the transfer efficiency (Figure 4)
Discussion
The genetic algorithm-optimized pulse sequence showed an improved performance in polarization transfer experiments over the BINEPT sequence, with a more than two times lower peak B1 amplitude. The feasibility of robust partial transfer of polarization was also demonstrated. The drawback is the computational complexity imparted by the spin-dynamics simulation for every cost function evaluation. However, for the [15N2] urea phantom and surface coil configuration used in these studies this took only a few hours on an average PC. This proposed approach could increase SNR in metabolic imaging studies9-16 where X nucleus hyperpolarization is detected via spin-coupled protons.Acknowledgements
This work was funded by Cancer Research UK Grants (C197/ A17242, C197/A16465, C9685/A25177) and by the European Union's Horizon 2020 Research and Innovation Program under FETOPEN grant agreement no. 858149.References
1. Wang J, Kreis F, Wright AJ, Hesketh RL, Levitt MH, Brindle KM. Dynamic 1H imaging of hyperpolarized [1-13C]lactate in vivo using a reverse INEPT experiment. Magnetic Resonance in Medicine 2018;79:741-7
2. von Morze C, Reed GD, Larson PE, Mammoli D, Chen AP, Tropp J, et al. In vivo hyperpolarization transfer in a clinical MRI scanner. Magnetic Resonance in Medicine 2018;80:480-7
3. Kreis F, Wright AJ, Somai V, Katz-Brull R, Brindle KM. Increasing the sensitivity of hyperpolarized [15N2]urea detection by serial transfer of polarization to spin-coupled protons. Magnetic Resonance in Medicine 2020;84:1844-56
4. Keeler J. Understanding NMR Spectroscopy. 2013
5. Bajpai P, Kumar M. Genetic Algorithm - an Approach to Solve Global Optimization Problems. Indian Journal of Computer Science and Engineering 2010;1:199-206
6. Khaneja N, Reiss T, Kehlet C, Schulte-Herbrüggen T, Glaser SJ. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. Journal of Magnetic Resonance 2005;172:296-305
7. Subrahmanian MV, Dregni AJ, Veglia G. Optimal design of offset-specific radio frequency pulses for solution and solid-state NMR using a genetic algorithm. Modern Magnetic Resonance 2018:605-15
8. Merkle H, Wei H, Garwood M, Uǧurbil K. B1-insensitive heteronuclear adiabatic polarization transfer for signal enhancement. Journal of Magnetic Resonance (1969) 1992;99:480-94
9. Gallagher FA, Woitek R, McLean MA, Gill AB, Manzano Garcia R, Provenzano E, et al. Imaging breast cancer using hyperpolarized carbon-13 MRI. Proceedings of the National Academy of Sciences 2020;117:2092
10. Chung BT, Chen HY, Gordon J, Mammoli D, Sriram R, Autry AW, et al. First hyperpolarized [2-13C]pyruvate MR studies of human brain metabolism. J Magn Reson 2019;309:106617
11. Wang ZJ, Ohliger MA, Larson PEZ, Gordon JW, Bok RA, Slater J, et al. Hyperpolarized 13C MRI: State of the Art and Future Directions. Radiology 2019;291:273-84
12. Chen H-Y, Aggarwal R, Bok RA, Ohliger MA, Zhu Z, Lee P, et al. Hyperpolarized 13C-pyruvate MRI detects real-time metabolic flux in prostate cancer metastases to bone and liver: a clinical feasibility study. Prostate Cancer and Prostatic Diseases 2020;23:269-76
13. Laustsen C, Nielsen PM, Qi H, Løbner MH, Palmfeldt J, Bertelsen LB. Hyperpolarized [1,4-13C]fumarate imaging detects microvascular complications and hypoxia mediated cell death in diabetic nephropathy. Scientific Reports 2020;10:9650
14. Guglielmetti C, Najac C, Didonna A, Van der Linden A, Ronen SM, Chaumeil MM. Hyperpolarized 13C MR metabolic imaging can detect neuroinflammation in vivo in a multiple sclerosis murine model. Proceedings of the National Academy of Sciences 2017:201613345
15. MacKenzie JD, Yen YF, Mayer D, Tropp JS, Hurd RE, Spielman DM. Detection of inflammatory arthritis by using hyperpolarized 13C-pyruvate with MR imaging and spectroscopy. Radiology 2011;259:414-20
16. Sriram R, Nguyen J, Santos JD, Nguyen L, Sun J, Vigneron S, et al. Molecular detection of inflammation in cell models using hyperpolarized 13C-pyruvate. Theranostics 2018;8:3400-7
Figures