3557
Convolutional Neural Networks for Super-resolution of Hyperpolarized 129Xe MR Images of the Lung1Medical Physics, Duke University, Durham, NC, United States, 2Biomedical Engineering, Duke University, Durham, NC, United States, 3Radiology, Duke University, Durham, NC, United States
Synopsis
Although hyperpolarized 129Xe gas exchange MRI enables imaging ventilation, barrier, and RBC components in a single breath-hold, the necessary under-sampling imposed by limited imaging time constrains image resolution. Therefore, it is common to acquire an additional dedicated ventilation scan, which increases cost and imaging time. Instead, we demonstrate that deep convolutional neural networks with template-based augmentation can be trained to transform under-sampled low-resolution 129Xe ventilation images to a level of detail comparable to that of a dedicated ventilation scan. We evaluate the performance of multiple super-resolution models based on signal-to-noise ratio and structural similarity.
Introduction
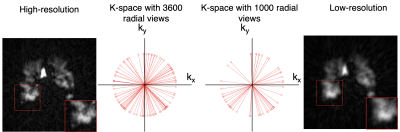
Although hyperpolarized 129Xe gas exchange MRI enables single-breath imaging of ventilation, barrier, and RBC components, the under-sampling imposed by limited scan duration constrains image resolution1. For example, radial Dixon imaging2 acquires ~ 1000 radial ventilation views vs. a dedicated scan that can be acquired with ≥3600 views. Therefore, an additional ventilation scan is typically ordered, despite increased cost and time. However, it may be possible to recover high-sampling-level quality from under-sampled Dixon-based ventilation images by exploiting recent advancements in convolutional neural networks (CNNs) for single image super-resolution (SISR)3. These deep learning models have been proposed to enhance image resolution for not only natural images but also MR images3. However, such methods have not been applied to 129Xe MRI. To this end, we created a training dataset for hyperpolarized 129Xe MRI and evaluate the performance of three SISR models, namely 1) SRCNN4 2) CSN5 and 3) RDN6. We demonstrate that these CNN models can largely recover high-resolution structure from under-sampled acquisitions, while even increasing SNR.Methods
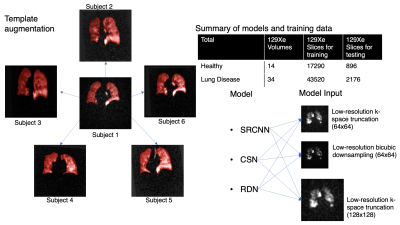
1) Dataset preparation and generation3D radial ventilation images were acquired at 3T (Siemens Magnetom Trio – VB19) on 48 subjects (14 healthy, 34 patients with lung disease) using the following parameters: views=3600; TR/TE=4.5/0.45ms; flip angle=1.5; FOV=40cm. The same subjects underwent 3D Dixon gas exchange MRI - using a randomized 3D Halton spiral radial sequence (views=1000, FOV=40cm). The high-resolution training targets were generated by reconstructing the full 3600-radial-views. All images were reconstructed to a 128x128x128 matrix from the k-space data using a kernel sharpness of 0.327 and clipped in the coronal direction to 128x128x64 to encompass only slices that contain the thoracic cavity.
Three low-resolution training datasets were created by a) reconstructing a 1000-radial-view subset of the k-space data (Fig. 1) b) down-sampling the resulting images from (a) by a factor of 2 via bicubic interpolation and c) down-sampling the high-resolution images (3600-radial-views) by a factor of 2 via bicubic interpolation. Although the down-sampling from method b) may seem superfluous, it is included to quantify information recovery in the simple down-sampling process.
The original 48 image volumes for training (3 low-resolution inputs, 1 high-resolution target) were increased 20-fold by template-based augmentation8. Here, all 3D volume were registered to 20 randomly selected 3D volumes from within the same set via deformable registration9 to yield 48x20x64 = 61,440 single-slice training examples (Fig. 2). Both the 48 original dedicated ventilation and Dixon ventilation image volumes were reserved as test datasets.
2) Model training
The 3 CNN models of increasing network complexity (SRCNN, CSN, and RDN) were implemented and tested. Each was trained to the high-resolution target using minibatches of 16 image patches of size 32x32 that were randomly extracted from the low-resolution image. Each model was implemented in Tensorflow-1 and trained on an NVIDIA Geforce RTX 3090 GPU for 500k steps. Training used the Adam optimizer10 with the default hyperparameters. The learning rate was initialized as 10-4 and underwent piecewise constant decay every 20,000 steps.
3) Data analysis
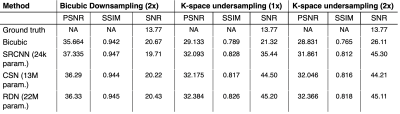
The performance of each network trained with each input dataset was evaluated by comparing SNR, peak-SNR (PSNR), and SSIM11 to that of simple cubic up-sampling of the low-resolution image. The SSIM was evaluated for only inside the thoracic cavity mask. SNR was calculated as the signal inside the thoracic cavity mask divided by the noise in the ROIs outside the mask. We then performed two-way RM-ANOVA and Tukey’s multiple comparison tests for each imaging metric to establish statistical differences in performance between models.
Results
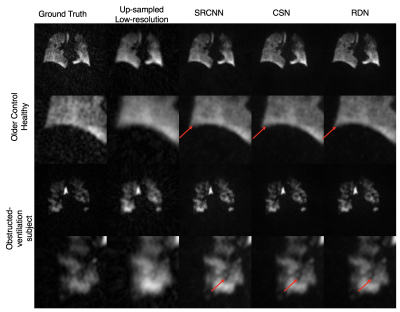
Figure 3 shows the images resulting from each of the models compared to the high-resolution ground truth in two subjects, one without, and one with ventilation defects. It demonstrates that each CNN increases the sharpness of the thoracic cavity boundary while also reducing the noise outside the lung. The small defect in the right lung is smeared out in the original low-resolution image but has been recovered by each of the models.Figure 4 summarizes the PSNR, SSIM, and SNR for each experiment. For columns 2 and 3, all CNN models have statistically significant higher PSNR and SSIM compared to the bicubic counterpart, indicating that each more faithfully reconstructs the high-resolution image compared to the standard upscaling of the low-resolution image. Moreover, for columns 2 and 3, each CNN model produces a significantly higher SNR than both the low-resolution image and the ground truth. This may indicate that the model is unable to map the noise from the under-sampled low-resolution image to the high-resolution output, suggesting that the super-resolution network has serendipitous denoising properties.
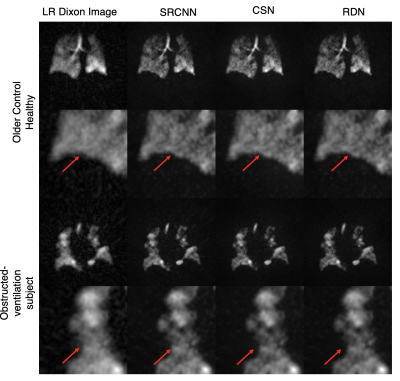
Moreover, despite not being trained on any of the Dixon image volumes, each model is able to produce sharper edges and accentuate ventilation defects (Figure 5).
Discussion
Quantitative comparison of PSNR, SSIM, and SNR demonstrate that each of these CNNs not only is capable of enhancing image resolution, but also significantly improves SNR. Notably, the relatively small SRCNN model achieved similar results to CSN and RDN in terms of PSNR and SSIM, suggesting that small networks may suffice for 129Xe MRI applications. Further work should include texture analysis of images for differentiating model performance, combining information from different degradation inputs, and extension to 3D networks.Acknowledgements
R01HL105643, R01HL12677, NSF GRFP DGE-1644868References
1. He, M. et al. Generalized Linear Binning to Compare Hyperpolarized 129Xe Ventilation Maps Derived from 3D Radial Gas Exchange Versus Dedicated Multislice Gradient Echo MRI. Acad. Radiol. 27, e193–e203 (2020).
2. Wang, Z. et al. Quantitative analysis of hyperpolarized 129Xe gas transfer MRI. Med. Phys. 44, 2415–2428 (2017).
3. Yang, W. et al. Deep Learning for Single Image Super-Resolution: A Brief Review. IEEE Trans. Multimed. 21, 3106–3121 (2019).
4. Dong, C., Loy, C. C., He, K. & Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 38, 295–307 (2016).
5. Zhao, X., Zhang, Y., Zhang, T. & Zou, X. Channel Splitting Network for Single MR Image Super-Resolution. IEEE Trans. Image Process. 28, 5649–5662 (2019).
6. Zhang, Y., Tian, Y., Kong, Y., Zhong, B. & Fu, Y. Residual Dense Network for Image Super-Resolution. Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit. 2472–2481 (2018). doi:10.1109/CVPR.2018.00262
7. Robertson, S. H. et al. Optimizing 3D noncartesian gridding reconstruction for hyperpolarized 129 Xe MRI-focus on preclinical applications. Concepts Magn. Reson. Part A 44, 190–202 (2015).
8. Tustison, N. J. et al. Convolutional Neural Networks with Template-Based Data Augmentation for Functional Lung Image Quantification. Acad. Radiol. 26, 412–423 (2019).
9. Avants, B. B., Tustison, N. J. & Johnson, H. Advanced Normalization Tools (ANTS). (2014).
10. Kingma, D. P. & Ba, J. L. Adam: A method for stochastic optimization. 3rd Int. Conf. Learn. Represent. ICLR 2015 - Conf. Track Proc. 1–15 (2015).
11. Wang, Z., Bovik, A. C., Sheikh, H. R. & Simoncelli, E. P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 13, 600–612 (2004).
Figures