3537

Removal of Partial Fourier-Induced Gibbs (RPG) Ringing artifacts in MRI

Hong-Hsi Lee¹, Dmitry S Novikov¹, and Els Fieremans¹
¹New York University School of Medicine, New York, NY, United States

Synopsis

Gibbs-ringing artifact in magnitude images obtained by using partial Fourier (PF) acquisition and zero filling interpolation is modeled analytically, and a correction pipeline based on modifying the local subvoxel-shifts method is proposed. With the understanding of oscillating convolution kernel due to the PF acquisition, the ringings in magnitude images can be robustly removed without the need of ad hoc image models and tuning parameters. The effects of ringings on diffusion metrics are further demonstrated in numerical phantoms and in vivo diffusion data. The proposed pipeline removes most ringings in magnitude images and stabilizes estimations of diffusion metrics.

Introduction

Gibbs-ringing in MR images results in signal oscillations around tissue boundaries and biases quantitative parameters, such as the diffusivity and kurtosis in diffusion MRI (dMRI)$$$\,$$$[1]. In case of fully sampled data, ringing is caused by the symmetric truncation of k-space$$$\,$$$[2,3] and can be robustly removed by local subvoxel-shifts$$$\,$$$[4]. In the case of partial-Fourier (PF) data, however, the asymmetric truncation of k-space$$$\,$$$[5] leads to additional ringing of wider intervals in the PF-sampling dimension that cannot be corrected solely based on magnitude images reconstructed via zero filling$$$\,$$$[4]. Here, we develop a pipeline for the Removal of PF-induced Gibbs-ringing (RPG) to remove ringing patterns of different periods by applying local subvoxel-shifts twice. The proposed pipeline is validated on numerical phantoms and demonstrated on in vivo dMRI measurements.

Method

$$$\bf{}Theory$$$
For PF acquisition of factor $$$pf$$$, k-space data is asymmetrically truncated at cutoffs $$$k=-\nu{}K_{\rm{}max}$$$ and $$$+K_{\rm{}max}$$$, where
$$\nu=2pf-1<1\,,\quad \frac{1}{2}<pf<1\,.$$
The Fourier transform of this k-space modulation yields a point spread function (PSF) $$$P_\nu(x)$$$ accounting for Gibbs-ringing patterns in image space:
$$P_\nu(x)\equiv\int_{-\nu K_{\rm{}max}}^{K_{\rm{}max}}\frac{{\rm{}d}k}{2\pi}e^{ikx}=\frac{1}{2\pi{}ix}\left(e^{iK_{\rm{}max}x}-e^{-I\nu{}K_{\rm{}max}x}\right)\,.\quad\quad(1)$$
This function has sinusoidal oscillations at both cutoffs, with periods $$$2\pi/K_{\rm{}max}$$$ and $$$2\pi/\nu{}K_{\rm{}max}$$$. Given that the voxel size $$$\Delta{}x=\pi/K_{\rm{}max}$$$ is half the smallest period, we see that the ringing patterns correspond to intervals
$$x_r=\Delta{}x$$
and
$$x_\nu=\frac{\Delta{}x}{\nu}=\frac{\Delta{}x}{2pf-1}>\Delta{}x\,.$$
Here we defined the $$$\it{}interval$$$ of a ringing pattern as the distance of peak-to-valley or valley-to-peak along x- and/or y-directions in the magnitude image.

The real part of the PSF in Eq.$$$\,$$$(1) is an even function that is nonzero at $$$x=0$$$. In contrast, the imaginary part of the PSF is an odd function that is equal to zero at $$$x=0$$$. For the most part, the ringing patterns arise by the convolution with PSF's real part,
$${\rm{}Re}\,P_\nu(x)=\frac{1}{2\Delta{}x}\left[{\rm{}sinc}\left(\pi\frac{x}{x_r}\right)+\nu\cdot{\rm{}sinc}\left(\pi\frac{x}{x_\nu}\right)\right]\,,$$
where $$${\rm{}sinc}(x)\equiv\sin{}x/x$$$. The first ringing pattern of interval $$$x_r$$$ is exactly the same as the ordinary Gibbs-ringing of fully sampled data, and the second ringing pattern has an interval $$$x_\nu$$$ wider than the first one. Here, we list $$$x_\nu$$$ for commonly used under-sampling factors:
$$x_\nu=\begin{cases}\frac{4}{3}\Delta{}x\,,&pf=7/8\,;\\2\Delta{}x\,,&pf=6/8\,;\\4\Delta{}x\,,&pf=5/8\,.\end{cases}$$

$$$\bf{}Ringing\,removal\,pipeline:\,SuShi\,vs\,RPG$$$

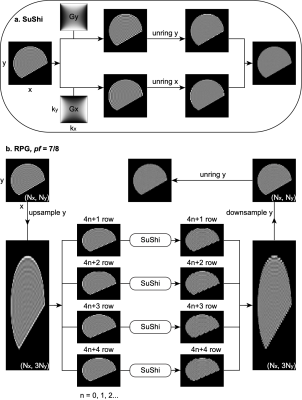
For fully sampled data, Figure 1a illustrates the 2D local Subvoxel-Shifts (SuShi) method for ringing removal$$$\,$$$[4]. In$$$\,$$$1D$$$\,$$$case,$$$\,$$$by$$$\,$$$shifting$$$\,$$$the$$$\,$$$image$$$\,$$$in$$$\,$$$a$$$\,$$$subvoxel$$$\,$$$level,$$$\,$$$the$$$\,$$$optimal$$$\,$$$shift$$$\,$$$for$$$\,$$$each$$$\,$$$voxel$$$\,$$$is$$$\,$$$individually$$$\,$$$determined$$$\,$$$by$$$\,$$$minimizing$$$\,$$$the$$$\,$$$local$$$\,$$$signal$$$\,$$$oscillations$$$\,$$$around$$$\,$$$the$$$\,$$$voxel,$$$\,$$$and$$$\,$$$the$$$\,$$$signal$$$\,$$$at$$$\,$$$the$$$\,$$$original$$$\,$$$position$$$\,$$$is$$$\,$$$linearly$$$\,$$$re-interpolated$$$\,$$$to$$$\,$$$the$$$\,$$$grid$$$\,$$$before$$$\,$$$shifting.$$$\,$$$To generalize to 2D, "weighting" filter functions $$$G_x\,,\,G_y$$$ with a saddle-like structure in Fourier domain were introduced$$$\,$$$[4]. After applying $$$G_x$$$ to the original image $$$I$$$, the ringing is suppressed in y-direction and enhanced in x-direction in the filtered image $$$I_x$$$, and vice versa for $$$G_y\,,\,I_y$$$. Removing ringings in $$$I_x$$$ using 1D local subvoxel-shifts along x-direction ("unring x") results in a corrected image $$$J_x$$$. Similarly, applying "unring y" to $$$I_y$$$ leads to a corrected $$$J_y$$$. Their sum yields the final corrected image $$$J=J_x+J_y$$$.
For $$$pf=7/8$$$ (Figure$$$\,$$$1b), to remove ringings of intervals $$$x_r=\Delta{}x$$$ and $$$y_\nu=\frac{4}{3}\Delta{}y$$$, we up-sample the original image by 3 fold in y-direction and divide it into 4 smaller sub-images and apply SuShi in each sub-image respectively. After combining corrected sub-images together and down-sampling the combined image by 3 fold in y-direction, we use "unring y" to remove remaining ringing of interval $$$y_r=\Delta{}y$$$.
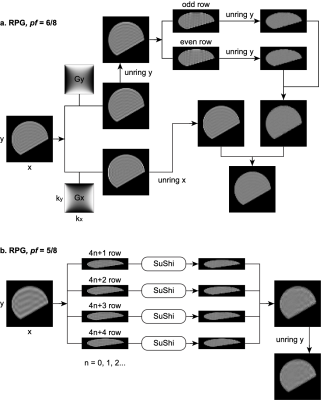
For $$$pf=6/8$$$ (Figure$$$\,$$$2a), we apply $$$G_x\,,\,G_y$$$ to the original image $$$I$$$, resulting in filtered images $$$I_x\,,\,I_y$$$. (1) We apply "unring y" to $$$I_y$$$ to remove ringing of interval $$$y_r=\Delta{}y$$$, yielding an intermediate image $$$J_y$$$. Then we divide $$$J_y$$$ into two sub-images and apply "unring y" to each of them to remove ringing of interval $$$y_\nu=2\Delta{}y$$$. Combining the two corrected sub-images, we obtain the first corrected image $$$\tilde{J}_y$$$. (2) We apply "unring x" to $$$I_x$$$ to remove ringing of interval $$$x_r=\Delta{}x$$$, leading to the second corrected image $$$J_x$$$. Finally, their sum yields the final output $$$J=\tilde{J}_y+J_x$$$.
For $$$pf=5/8$$$ (Figure$$$\,$$$2b), to remove ringings of intervals $$$x_r=\Delta{}x$$$ and $$$y_\nu=4\Delta{}y$$$, we divide the original image into 4 sub-images and apply SuShi to 4 sub-images respectively. After combining sub-images together, we use "unring y" to remove remaining ringing of interval $$$y_r=\Delta{}y$$$.

$$$\bf{}Numerical\,simulation$$$
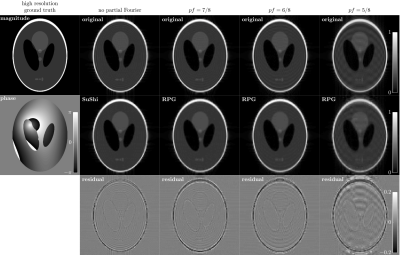
We created a 2D Gibbs-ringing phantom by taking the center k-space data ($$$90\times90$$$ matrix), defining the range $$$k_{x,y}\in\left[-K_{\rm{}max},+K_{\rm{}max}\right]$$$, of a ground truth image of a $$$900\times900$$$ Shepp-Logan phantom with additional phase$$$\,$$$[6] (Figure$$$\,$$$3). The center k-space data was further zeroed in $$$k_y\in\left[-K_{\rm{}max},-\nu K_{\rm{}max}\right]$$$ to simulate the data of PF acquisition ($$$pf=7/8,6/8,5/8$$$) in the phase-encoding direction. We did not recover zeroed k-space data using PF reconstruction; instead, we applied Fourier transform and took magnitude images.

$$$\bf{}In\,vivo\,MRI$$$
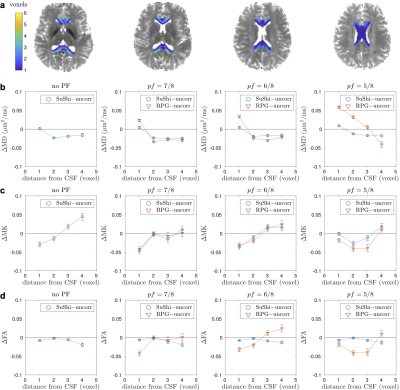
A 27-year-old female underwent imaging on a 3T Siemens Prisma with a 20-channel head coil after providing consent. dMRI measurements using monopolar pulsed-gradient spin-echo sequence were repeated for fully sampled data and PF acquisition ($$$pf=7/8,6/8,5/8$$$). Images were reconstructed via zero filling. For each scan, we obtained 4 b=0 images and 84 diffusion-weighted-images of b=[0.25,1,2]ms/$$$\mu$$$m$$$^2$$$. Resolution$$$=1.7\times1.7\times3$$$mm$$$^3$$$. TR/TE=3700/96ms. Maps of mean diffusivity (MD), fractional anisotropy (FA), and mean kurtosis (MK) were calculated$$$\,$$$[7].

Ringings in above images were removed using RPG.

Results

For magnitude images of the numerical phantom, the RPG pipeline robustly removes Gibbs-ringings due to PF acquisitions of $$$pf=7/8,6/8\,$$$(Figure$$$\,$$$3). For $$$pf=5/8$$$, the corrected image still has ringings.

For in vivo data, the RPG pipeline corrects the underestimated MD values in white matter around ventricles due to PF-induced Gibbs-ringing of $$$pf=7/8,6/8\,$$$(Figure$$$\,$$$4). For $$$pf=5/8$$$, the MD map after applying RPG looks blurred.

The effect of ringing removal (SuShi/RPG) on MD/FA/MK in corpus callosum is shown in Figure 5.

Discussion and Conclusions

RPG$$$\,$$$corrects$$$\,$$$Gibbs-ringing$$$\,$$$artifacts$$$\,$$$in$$$\,$$$PF-acquired$$$\,$$$magnitude$$$\,$$$MRI$$$\,$$$with$$$\,pf=7/8,6/8$$$,$$$\,$$$thereby$$$\,$$$removing$$$\,$$$the$$$\,$$$bias$$$\,$$$in$$$\,$$$quantitative$$$\,$$$MR$$$\,$$$metrics.$$$\,$$$For$$$\,pf=5/8$$$,$$$\,$$$RPG$$$\,$$$ringing$$$\,$$$removal$$$\,$$$leads$$$\,$$$to$$$\,$$$excessive$$$\,$$$image$$$\,$$$blurring$$$\,$$$due$$$\,$$$to$$$\,$$$the$$$\,$$$interaction$$$\,$$$between$$$\,$$$image$$$\,$$$phase$$$\,$$$map$$$\,$$$and$$$\,$$$complex$$$\,$$$PSF$$$\,$$$in$$$\,$$$Eq.$$$\,$$$(1)$$$\,$$$(we$$$\,$$$only$$$\,$$$consider$$$\,$$$its$$$\,$$$real$$$\,$$$part$$$\,$$$contribution$$$\,$$$in$$$\,$$$RPG$$$\,$$$pipeline).$$$\,$$$Considering$$$\,$$$the$$$\,$$$benefit$$$\,$$$of$$$\,$$$PF$$$\,$$$acquisition$$$\,$$$and$$$\,$$$the$$$\,$$$feasibility$$$\,$$$of$$$\,$$$ringing$$$\,$$$removal,$$$\,$$$we$$$\,$$$suggest$$$\,$$$applying$$$\,$$$PF=6/8,$$$\,$$$which$$$\,$$$is$$$\,$$$already$$$\,$$$adopted$$$\,$$$as$$$\,$$$the$$$\,$$$default$$$\,$$$in$$$\,$$$dMRI$$$\,$$$protocols$$$\,$$$of$$$\,$$$many$$$\,$$$large$$$\,$$$studies,$$$\,$$$e.g.,$$$\,$$$Human$$$\,$$$Connectome$$$\,$$$Project$$$\,$$$[8],$$$\,$$$Adolescent$$$\,$$$Brain$$$\,$$$Cognitive$$$\,$$$Development$$$\,$$$study$$$\,$$$[9],$$$\,$$$and$$$\,$$$UK$$$\,$$$Biobank$$$\,$$$[10].

Acknowledgements

Research was supported by the National Institute of Neurological Disorders and Stroke of the NIH under awards R01 NS088040 and R21 NS081230, and was performed at the Center of Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), an NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).

References

1. Veraart, J., Fieremans, E., Jelescu, I. O., Knoll, F., & Novikov, D. S. (2016). Gibbs ringing in diffusion MRI. Magnetic resonance in medicine, 76(1), 301-314.

2. Henry Wilbraham. On a certain periodic function. The Cambridge and Dublin Mathematical Journal, 3:198–201, 1848.

3. Willard Gibbs. Fourier’s series. Nature, 59(1522):200, 1898.

4. Elias Kellner, Bibek Dhital, Valerij G Kiselev, and Marco Reisert. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magnetic resonance in medicine, 76(5):1574–1581, 2016.

5. G McGibney, MR Smith, ST Nichols, and A Crawley. Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI. Magnetic resonance in medicine, 30(1):51–59, 1993.

6. Mark Chiew. Partial Fourier. https://users.fmrib.ox.ac.uk/~mchiew/docs/PartialFourier.html.

7. Jensen, J. H., Helpern, J. A., Ramani, A., Lu, H., & Kaczynski, K. (2005). Diffusional kurtosis imaging: the quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 53(6), 1432-1440.

8. Sotiropoulos, S. N., Jbabdi, S., Xu, J., Andersson, J. L., Moeller, S., Auerbach, E. J., ... & Feinberg, D. A. (2013). Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage, 80, 125-143.

9. Casey, B. J., Cannonier, T., Conley, M. I., Cohen, A. O., Barch, D. M., Heitzeg, M. M., ... & Orr, C. A. (2018). The adolescent brain cognitive development (ABCD) study: imaging acquisition across 21 sites. Developmental cognitive neuroscience, 32, 43-54.

10. Alfaro-Almagro, F., Jenkinson, M., Bangerter, N. K., Andersson, J. L., Griffanti, L., Douaud, G., ... & Vidaurre, D. (2018). Image processing and Quality Control for the first 10,000 brain imaging datasets from UK Biobank. Neuroimage, 166, 400-424.

Figures

Fig 1. Removing Gibbs-ringing in 2D images. a. Ordinary local subvoxel-shifts (SuShi) pipeline [3] for the fully sampled data. b. Removal of PF-induced Gibbs-ringing (RPG) of pf = 7/8.

Fig 2. Removing Gibbs-ringing in 2D images (continued). a. RPG of pf = 6/8. b. RPG of pf = 5/8.

Fig 3. Numerical simulations of Gibbs-ringing removal in 2D magnitude images of the Shepp-Logan phantom with phase. The first two rows show images of the signal magnitude before and after ringing removal, and the third row shows residual maps. For pf = 7/8 and 6/8, the RPG pipeline robustly removes PF-induced ringings, whereas for pf = 5/8 the corrected image still has non-trivial amount of ringings after applying RPG, potentially caused by the interaction of the images phase in high resolution ground truth and the convolution kernel in Eq. (1).

Fig 4. Mean diffusivity (MD) map baed on diffusion-weighted-images (DWIs) before and after Gibbs-ringing removal using local subvoxel-shifts (SuShi) and RPG, with the residual of MD before and after corrections. The unit of MD is $$$\mu$$$m$$$^2$$$/ms.

Fig 5. The differences of MD, MK, and FA before and after ringing removal in a. corpus callosum (CC) ROIs consisting of voxels distant from the ventricles by 1-6 voxels. b-d. The MD, MK and FA were calculated based on b=0 images and DWIs before and after ringing removals using SuShi or RPG pipeline. The "uncorr" denotes uncorrected data. The SuShi only slightly corrected the underestimated MD in CC voxels close to ventricles. In contrast, the RPG resulted in stronger corrections on the underestimated MD in these voxels. Further, FA and MK decreased after ringing removal using SuShi or RPG.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

3537