3536
Ringing Artifacts Reduction with Low-Pass Filtered Deblurring Kernels
Dinghui Wang1 and James G. Pipe1
1Radiology, Mayo Clinic, Rochester, MN, United States
1Radiology, Mayo Clinic, Rochester, MN, United States
Synopsis
Spiral imaging has been used in many applications for its fast imaging speed, high scan efficiency and low sensitivity to motion. However, ringing artifacts are often observed in regions where the field map Δf0 changes rapidly in space, especially with long spiral readouts. The goal of this work is to address this issue with a modified deblurring model that weights more on low spatial frequencies. Simulation and volunteered data have demonstrated that the ringing artifacts can be substantially reduced by the proposed method.
I. Introduction
Spiral imaging has many favorable characteristics such as fast imaging, high SNR efficiency and low sensitivity to motion. It has been implemented for high resolution brain imaging1 along with the advancements in the spiral Dixon technique2. However, deblurring remains challenging in regions where the field map Δf0 changes rapidly in space, especially with long spiral readouts3. At the highest spatial frequencies in k-space, accumulated phase differences among adjacent voxels could reach or exceed 180 degree in these regions. Furthermore, intra-voxel de-phasing will also cause magnitude decay of the signal. Both factors contribute to ringing artifacts. Theoretically, modeling4,5 of the intra-voxel de-phasing in the deblurring algorithm would mitigate the ringing artifacts. However, it can be challenging to establish an accurate model in practice because the exact distribution of Δf0 are often difficult to estimate. In this study, we propose to use a modified deblurring model that adaptively increases the weighting of low spatial frequencies to mitigate the ringing artifacts.II. Theory
The deblurred images can be obtained by iteratively solving$$$B^HBf = B^Hg$$$. (1)
in which g represents the blurred TE image(s) and f represents the underlying true image(s). For spiral water-fat imaging, g presents the water and fat images. B is the procedure of the blurring, while BH is conjugate transpose of B. Instead of using operations on large matrices, the processes B and BH are computed by spatially varying image-space convolution using blurring and deblurring kernels, respectively2. We propose to modify equation (1) to
$$$(LB)^H(LB)f = (LB)^HLg$$$. (2)
where L is a low-pass filter. Eq. (2) can be solved iteratively similarly as (1). The kernels corresponding to LB are the low-pass filtered version of kernels corresponding to B.
III. Methods
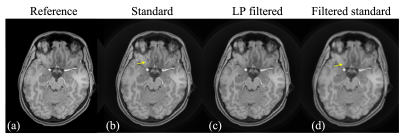
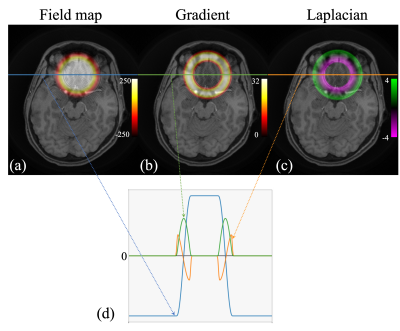
SimulationSimulation was performed for a water image (figs.1-2). The field map Δf0 has a localized rapidly varying region as shown in fig.2 (a). The peak magnitude of the gradient of Δf0 reaches 31.3 Hz/pixel (fig.2(b)). Spiral k-space data were simulated using a discrete Fourier transform with four times spatial oversampling, from which the blurred image at TE = 0 ms were reconstructed. The readout length of the spiral trajectories was 16.3 ms.
Data acquisition
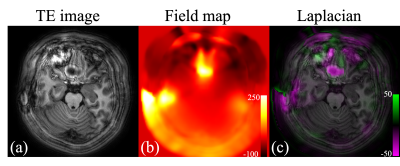
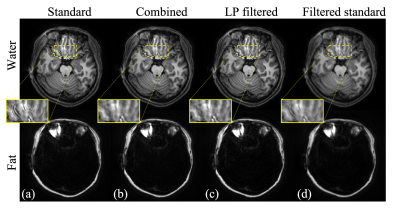
Volunteer brain images were acquired on 3T Philips scanners (Philips Healthcare, Best, The Netherlands). A 3D T1-weighted MP-RAGE data set was collected with distributed spiral trajectories6. The resolution was 1 mm by 1 mm by 2 mm. The spiral readout length was 19.7 ms. Data at two TEs with ΔTE = 1.15 ms were collected for water-fat imaging. A 2D T2-weighed spin-echo data set with fat-suppression was also acquired. The in-plane resolution was 1 mm by 1mm with slice thickness of 4 mm. The spiral readout length was 45 ms. The Field maps of Δf0 were obtained from separate low-resolution scans.
Reconstruction
Blurred TE images were reconstructed by standard gridding methods. Next, deblurred images were computed with the standard model described by Eq. (1) and the proposed model by Eq. (2) respectively. A Hanning window of a diameter of 90% of the k-space was used for the low-pass filter L. Masks were computed based on the product of the magnitude of laplacian of Δf0 and the spiral readout length to combine the two sets of results. The results from the standard method were also low-pass filtered using the same filter L for comparison.
IV. Results and Discussion
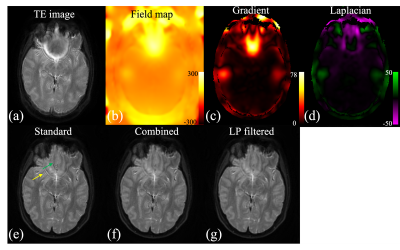
In the simulation results shown in fig.1, the ringing artifacts are substantially mitigated by deblurring using the proposed model. The residual ringing of the proposed method is significantly less than the ringing in the low-pass filtered images from the standard method (pointed by yellow arrows), yet the resolution reduction of the latter is much more evident than the former. The simulation has also demonstrated that the ringing artifacts start to occur near the peaks and valleys of the Laplacian of the field map Δf0 as shown in fig. 2.Results from the volunteer data (figs.3-5) are are consistent with the simulation results. Similarly, deblurring using the proposed model reduces the ringing artifacts. The images are much sharper than the low-pass filtered result of standard deblurring. The overall resolution is further preserved by combining the results from the standard method and the proposed deblurring, using masks determined based on the readout length and the laplacian of Δf0. There are some residual ringings when readout length is 45 ms as shown in fig. 5. Incorporating an intra-voxel de-phrasing model might further improve the performance.
Acknowledgements
This work was funded by Philips Healthcare.References
1. Li Z, et al. A spiral spin-echo MR imaging technique for improved flow artifact suppression in T1-weighted postcontrast brain imaging: A comparison with cartesian turbo spin-echo. Am J Neuroradiol. 2016; 37 (4):642-7.
2. Wang D, Zwart NR, Pipe JG. Joint water-fat separation and deblurring for spiral imaging. Magn Reson Med. 2018;79:3218-3228.
3.Noll DC, Fessler JA, Sutton BP. Conjugate phase MRI reconstruction with spatially variant sample density correction. IEEE Trans Med Imaging 2005;24:325–336.
4.Yablonskiy AD, Sukstanskii AL, Luo J, Wang X, Voxel spread function method for correction of magnetic field inhomogeneity effects in quantitative gradient-echo-based MRI, Magn Reson Med. 2013; 70(5): 1283–1292, 2013.
5.Ngo G, Cerjanic A, Sutton BP, Improved image quality for long readout imaging using piecewise linear field map model. in proceeding of the 28th Science Meeting of ISMRM, Paris, France, 2018. Abstract 175.
6. Turley D, Pipe JG. Distributed spirals: A new class of three-dimensional k-space trajectories. Magn Reson Med. 2012; 70(2): 413-419.
Figures
Figure 1 Comparison of the simulation results. A reference water image (a) was used in the simulation. Ringing artifacts (yellow arrow) can be seen in the deblurred image (b) using the standard deblurring method, which are mitigated using the proposed deblurring method with low-pass filtered deblurring kernels (c). A simple low-pass filtering (d) of the image in (b) does not mitigate the ringing to the same extent.
Figure 2 Relationship of field map and ringing artifacts. Field map (in the range of [-250, 250] Hz) (a), magnitude of the gradient of the field map (in the range of [0, 32] Hz/pixel) (b) and the Laplacian of the field map (in the range of [0, 4] Hz/pixel2) (c) are overlaid on the image of the standard deblurred image. Their values through a horizontal line are plotted in (d). Note that the ringing artifacts start to occur near the peaks and valleys of the Laplacian.
Figure 3 3D MPRAGE brain data. Laplacian of the field map Δf0 is used to identify regions tend to have ringing artifacts. (a) one of the TE images. (b) Δf0 in the range of [-100, 250] Hz. (c) Laplacian of the field map Δf0 overlaid on the TE image (a).
Figure 4 Comparison of results. A mask computed based on the Laplacian of Δf0 was used to combine the results of the standard deblurring (a) and the proposed method (c). The combined results are shown in (b). Water and fat in (a) were also low-pass filtered (d). Note that the residual ringing inside the yellow boxes is significantly less in (c) (d) compared to (d).
Figure 5 Results of 2D T2-weighted images with spiral readout length of 45 ms. (a) is the blurred TE image. the field map and and its gradient and laplacian are shown in (b)-(d), respectively. A mask computed based on the Laplacian of Δf0 (d) was used to combine the results of the standard deblurring (e) and the deblurring with low-pass filtered kernels (g). The combined results are shown in (f). The ringing artifacts (pointed by the arrows) in (e) are mitigated in (f) and (g).