Introduction

Gibbs ringing artefacts are a ubiquitous feature of MR images. They can mask genuine features in the images, and make quantification unreliable when different images are used jointly in fitting procedures. Filtering is employed routinely on MRI scanners, and provides effective mitigation of the artefacts at the expense of resolution. Alternative approaches have been proposed to reduce these artefacts, including extrapolation of data outside of the acquired region of k-space [1-3], machine learning approaches [4], and the use of subvoxel shifts [5].
This study focuses on the subvoxel shifts method, which has become more widely used over the last few years due to its simplicity and computational efficiency. This method relies on the suppression of Gibbs ringing artefacts in 1D by shifting the sampling points of an acquired line using the Fourier shift theorem, so as to find the subvoxel shift that minimises the amount of oscillation in the immediate vicinity of a given point of interest. Once this optimal shift is identified, the intensity at the point of interest is obtained by linear interpolation of the two nearest resampled points back to the original sampling location.
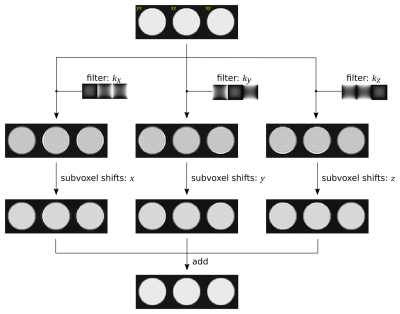
This is extended to 2D images by judicious use of filtering in the Fourier domain, in a way that attenuates high frequencies along a given axis while amplifying high frequencies along the perpendicular axis. After filtering, each line of the image along the direction of high frequency amplification is processed independently to remove ringing artefacts using the 1D subvoxel shifts procedure. This is repeated in the orthogonal direction, and the two resulting images are added together to produce the final image with vastly reduced ringing artefacts.
However, one of the limitations of the original proposal is that it operates in 2D, making it unsuitable for 3D volumetric acquisitions. The aim of this study is to extend the technique to the 3D domain.

Methods

The extension of this method to 3D is illustrated in Figure 1, and consists of the following simple modifications: (i) the filtering and 1D subvoxel shifts are applied in all 3 axes separately; and (ii) the filters are modified to match the 3D nature of the problem, as described below.
For the method to work as intended, the filters need to satisfy two requirements: (i) they must sum to one to ensure preservation of the overall spatial frequency content of the image following the final summation and so preserve image resolution; and (ii) each filter needs to effectively suppress ringing artefacts in directions orthogonal to the direction along which the subvoxel shifts are to be applied. The filters proposed in the original 2D technique take the form $$$G_x=C_y/(C_x+C_y)$$$ and $$$G_y=C_x/(C_x+C_y)$$$ and where $$$C_i=1+cos(k_i/k_i^{max})$$$ (the Hahn function). For the 3D case, we propose to modify the filters to take the form: $$$G_x=C_y C_z/(C_x C_y+C_x C_z+C_y C_z)$$$, and similarly for $$$G_y$$$ & $$$G_z$$$, satisfying the requirements laid out above.
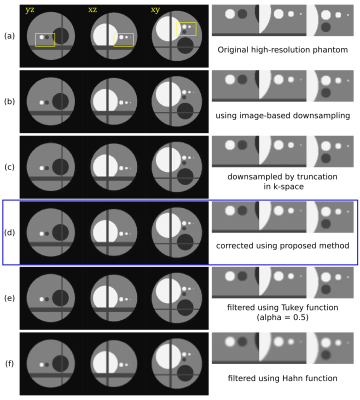
These modifications were assessed using a numerical phantom, produced by Fourier transform truncation of a high-resolution image. Various levels of noise were then added to the image in the complex domain, followed by magnitude transformation to produce images with realistic artefacts. For comparison, the high-resolution original image was also downsampled in the image domain to yield an image free of ringing artefacts (using the MRtrix3 mrgrid command). In addition, images were also produced by truncation in the Fourier domain with filtering using Tukey ($$$\alpha=0.5$$$) and Hahn functions respectively.
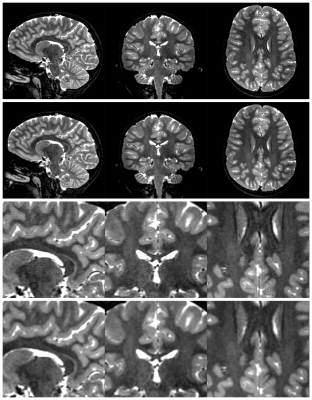
To investigate the effectiveness of the proposed method in practice, a 3D T2-weighted scan was also processed (Philips Achieva 3T, Turbo Spin Echo, TR=2500ms, TE=350ms, FA=90°, 1mm isotropic voxel size, 188×240×240 matrix, no filtering), and the results assessed by visual inspection.

Results & discussion

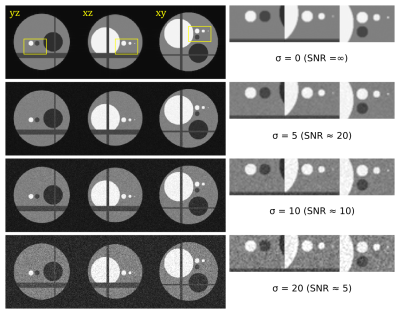
The results obtained using the 3D numerical phantom are shown in Figures 2 & 3. The lower-resolution image obtained using simple truncation of k-space contains significant Gibbs ringing artefacts compared to the equivalent image obtained via image-based downsampling, as expected. The proposed method suppresses these artefacts very effectively, while preserving image resolution. For comparison, filtering in the Fourier domain using Tukey ($$$\alpha=0.5$$$) and Hahn functions are shown, showing good suppression of ringing artefacts but with the expected loss of resolution.
The method is robust to noise, with the images produced remaining faithful to the original down to SNR=5 (Figure 3). Note that small details in the images are preserved using this approach, and remain clearly visible even in the presence of noise.
In the in vivo brain data, Gibbs ringing artefacts can clearly be seen in the original image, which are effectively suppressed using the proposed approach. Processing time for this dataset was 4.5s on an AMD Ryzen 9 3950X 16-Core CPU running Arch Linux.

Conclusion

The method of subvoxel shifts for removal of Gibbs ringing artefacts can trivially be extended to 3D, and shares many of the same properties. It is effective and computationally efficient, and will hopefully prove useful in applications where these artefacts are currently problematic.

Acknowledgements

This work was supported by ERC grant agreement no. 319456, by core funding from the Wellcome/EPSRC Centre for Medical Engineering [WT203148/Z/16/Z] and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London and/or the NIHR Clinical Research Facility. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health and Social Care.