Introduction

Diagnostic capabilities of diffusion magnetic resonance imaging (dMRI) are largely dependent on the gradients used to encode the thermal motion of water molecules within biological tissue. Advancements in gradient hardware have the potential to broaden the clinical role of dMRI, however, image quality suffers from eddy currents induced by strong diffusion encoding gradients¹. A variety of correction techniques exist that aim to correct the effects of eddy currents, including the post-processing technique “eddy” offered by the software library FSL. With this approach, corrections to data are made by accounting for eddy currents whose behaviors are characterized by long time constants, or in other words are approximately static in time². While generally effective for the traditional Pulsed Gradient Spin Echo (PGSE) diffusion sequence, this correction method does not necessarily apply to advanced forms of dMRI, such as Oscillating Gradient Spin Echo (OGSE)³. In this work, the performance of an in-house algorithm which, contrary to existing approaches, includes an exponential term with a finite time-constant to model eddy currents that decay on shorter time scales (Eq. 1), was evaluated by correcting in-vivo PGSE and OGSE brain images and comparing correction quality with existing correction methods. $$A_{\tau,i}e^{-t/\tau_i} + A_{inf,i}\qquad(1)$$
where A_𝜏,i and A_inf,i are eddy current amplitudes, 𝜏_i is a finite time-constant, and i = {0,x,y,z} corresponds to the B₀, G_x, G_y, and G_z eddy currents, respectively.

Methods

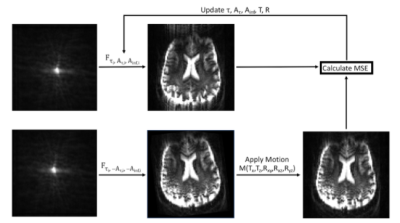
Opposite polarity diffusion gradients produce distortions that are equal in magnitude, but opposite in direction⁴. Accordingly, the algorithm iteratively takes image pairs acquired with opposite polarity diffusion gradients and applies identical yet inverse corrections to the data based on Eq. 1, until the mean squared error is minimized, as outlined in Figure 1. Two healthy male subjects were scanned on a 7T head-only MRI (Siemens). Single-shot echo-planar imaging (EPI) diffusion MRI data was acquired using PGSE (0Hz) and cosine modulated trapezoidal OGSE (40Hz). The OGSE frequency was based on optimized diffusion dispersion sequence parameters determined by Arbabi et al⁵. The remaining parameters were 4 directions at b = 750 s/mm², 6 averages, echo time = 124 ms, field of view = 224 × 224 mm², 2 mm isotropic resolution, 40 slices of 2 mm thickness and scan time 9.5 minutes. The spatially varying field dynamics up to third order in space were also measured after image acquisitions using a field monitoring system (Skope) to validate the performance of the algorithm by comparing it to a new gold standard correction tool. Images were corrected using FSL eddy, the algorithm’s time-constant (TCEDDY; Eq. 1 A_inf,i only) and time-varying (TVEDDY; Eq. 1) versions, and field monitoring (FM) using all acquired spatial orders and an iterative model-based reconstruction approach. Correction quality was assessed by comparing the mean square error between corrected pairs of images. Additionally, to validate the corrections made by the algorithm, field monitored eddy current phase variations of the zeroth and first order were used to simulate eddy-current distorted raw data, that was then processed using TCEDDY and TVEDDY. The algorithm’s zeroth and first order corrections were then compared to the ground truth eddy current phase deviations to assess correction accuracy.

Results

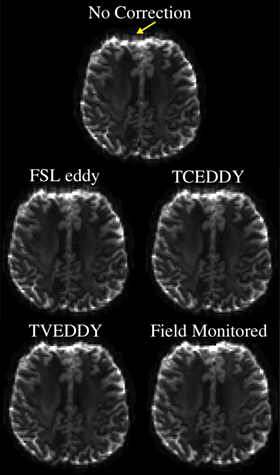
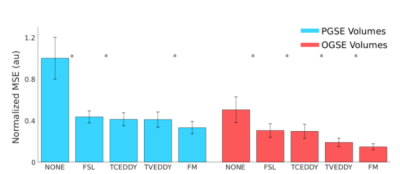
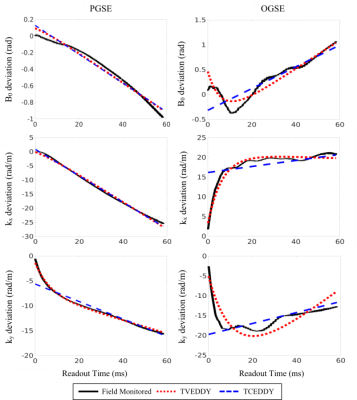
In the uncorrected OGSE image (Fig. 2), blurring is seen to extend past the edges of the frontal lobe, which is still apparent after correction with FSL eddy and TCEDDY. This artifact is reduced significantly using the time-varying eddy current model, which is qualitatively comparable to the field monitored correction. In Figure 3, decreasing average MSE values are reported for FSL eddy correction, TCEDDY, TVEDDY, and FM respectively. Statistically significant changes in MSE (p < 0.01) were observed between subsequent correction techniques, excluding the comparison between the PGSE correction using TCEDDY and TVEDDY. Comparison of the correction profiles to the ground truth (Fig. 4) shows how both approaches accurately correct PGSE distortions, but only TVEDDY partially corrects the time varying eddy currents observed for OGSE.

Discussion

In PGSE volumes, there was no significant difference between correction with TVEDDY or TCEDDY which is consistent with the conventional assumption that modelling eddy current decay is not necessary for PGSE, as the linear phase shifts are adequately handled using a static eddy current model. Figure 4 further illustrates how eddy current distortions from PGSE sequences generally exhibited linear behavior that could be modelled using a single exponential term with an infinite decay constant (TCEDDY). Conversely, the OGSE distortions displayed more complex eddy current evolution which are not accurately characterized by single-term exponentials. They are better captured using TVEDDY, where an additional eddy current term with a finite time constant provides additional degrees of freedom to correct for time-varying eddy currents. Overall, this resulted in reduced image blurring for OGSE volumes (Fig. 2), which has the potential to improve robustness of diffusion metric analysis.

Conclusion

This work presented and validated a new computational method for correcting diffusion gradient eddy currents that notably outperforms FSL eddy for OGSE acquisitions. The capacity to correct distortions induced by advanced dMRI techniques without the substantial cost of a field monitoring system will promote the development and clinical application of dMRI.