Introduction

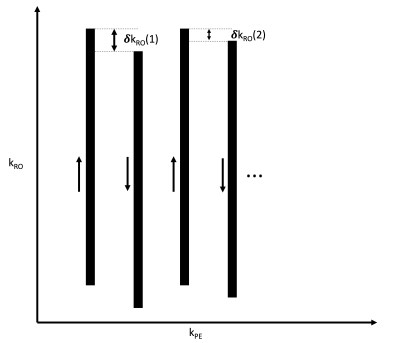
Nyquist ghosting arising from mis-alignment of k-space lines in echo-planar imaging (EPI) [1] is a well-known and characterized issue (figure 1). In modern clinical MRI scanners, the eddy currents responsible for this effect, induced by fast gradient switching, are usually well understood, and a correction scheme based on navigator measurement of the linear phase term between forward and reverse read-out lines is normally sufficient to suppress the image artefact. However, at ultra-high field strength such as 7T, EPI Nyquist ghosting has again become a concern. In this work we explore dynamic variation of the linear phase term across the EPI read-out train, through computer simulations and acquired experimental data. In the presence of such effects, existing correction methods will not be sufficient. In particular, we consider temporal oscillations of linear phase and identify two distinct effects from such oscillations: i) offset between the navigator-measured linear phase and the average linear-phase in the read-out train, ii) line-by-line variation in the linear-phase. The objective of this work is to characterize and understand these effects in more detail, and to show the observation of such effects in exploratory data acquired on 3T and 7T systems. Explicit line-by-line correction of phase appears to improve, but not completely resolve, the ghosting observed.

Methods

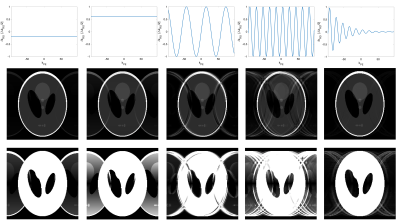
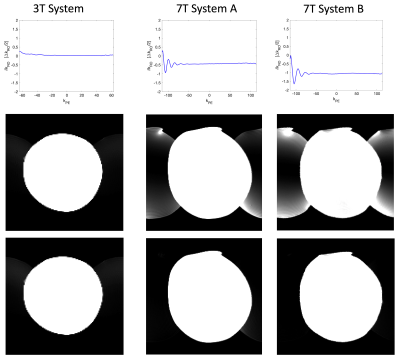
Simulated data: the effect of offset and oscillations in the linear phase term δk_RO across the EPI read-out train was calculated in Matlab using the standard digital (Shepp-Logan) phantom at a matrix size of 230x230. Different oscillation frequency, amplitude, and damping was applied, with the resulting ghosting evaluated visually as well as quantified using ghost-to-image signal ratio and RMSE.
Experimental: a phantom was scanned using an unaccelerated spin-echo single-shot EPI with transverse orientation and right-left phase encoding direction, both on 3T (Siemens MAGNETOM Prisma) with 128x128 matrix and at 7T (Siemens MAGNETOM Terra) with 230x230 matrix. Both protocols used an echo-spacing of 1 ms. Each experiment was repeated twice; once with phase-encoding (PE) enabled and once disabled, in order to collect repeated phase-reversed ‘navigator’ lines for the whole of k-space. Using the second dataset with PE disabled, we calculated the linear phase between each pair of forward/reverse read-out lines throughout the whole EPI train. These values were then subtracted to the navigator-measured linear-phase δk_RO,nav and plotted as function of k_PE. Finally, the default navigator-based reconstruction of the first dataset with PE enabled was compared to a modified reconstruction where the linear phase was corrected according to the line-by-line measurement.

Results

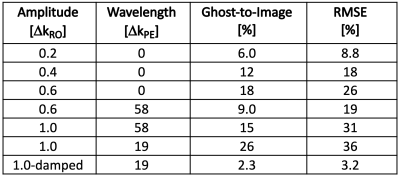
Example simulations are shown in figure 2 for linear and oscillating phase offsets, and ghost-to-image ratios as well as root-mean-squared-error (RMSE) values are listed in table 1. Significant visual ghosting correlates with a ghost-to-image ratio of above 10%, whereby image quality is substantially reduced. Already at a δk_RO value of 0.2 Δk_RO, corresponding to a time delay of less than 1μs in our experimental protocol, the ghost-to-image ratio exceeds 5%. The ghosting arising from oscillating phase offset gives a more complex artefact, with increased severity at higher frequency (table 1). A damped oscillation, as expected, contributes less overall ghosting dependent on the decay constant relative to the acquisition of the echo train. Experimental data from the non-phase-encoded readout train at 7T shows the presence of both an overall offset, and a damped oscillating term. This was observed to be similar on two different 7T systems, whereas equivalent analysis of 3T data showed essentially no net offset or oscillation (figure 3). Correspondingly, the ghosting observed for standard navigator-correction was clearly greater for the 7T systems. Reconstruction of the 7T images using explicit correction of each line pair using the non-PE data resulted in a substantial reduction of observed ghosting.

Discussion and Conclusion

Navigator-based methods for correction of Nyquist-ghosting in EPI assume that the misalignment between forward and reverse PE-lines is constant throughout the whole EPI read-out train. In this work, observed Nyquist ghosting indicates that this is not necessarily the case in ultra-high field systems. Conventional 3-line navigator algorithms for phase correction are insufficient to capture any oscillating component, and as an indirect result may not correctly capture the overall linear offset. Correction using explicit line pairs from the whole echo train leads to improvement in image quality, as illustrated in figure 3. This can be implemented by adding a separate reference scan (with PE disabled) at the beginning of the sequence. However, in practice it may prove difficult to ensure sufficient accuracy of the phase measurement for all slices and coil elements. Hybrid solutions with extended or integrated navigators are also possible. This study only considered unaccelerated single-shot EPI with relatively long echo-spacing of 1 ms, where oscillations were damped before passing through k_PE = 0; accelerated versions reaching k_PE= 0 much sooner may therefore accentuate the ghosting. Further work needs to be carried out in order to characterize this issue in more detail and identify the source. Based on our independent measurement at two different 7T MR systems, it seems plausible that this is not due to any system-specific miscalibration of the gradient system, and will require implementation of specific phase-correction algorithms.

Acknowledgements

We would like to thank David Porter and Graeme Keith at the University of Glasgow for data acquisition on one of the 7T systems.