3526
FID-navigated phase correction for multi-shot 3D EPI acquisitions
Tess E Wallace1,2, Tobias Kober3,4,5, Simon K Warfield1,2, and Onur Afacan1,2
1Computational Radiology Laboratory, Boston Children's Hospital, Boston, MA, United States, 2Radiology, Harvard Medical School, Boston, MA, United States, 3Advanced Clinical Imaging Technology, Siemens Healthcare, Lausanne, Switzerland, 4Radiology, Lausanne University Hospital and University of Lausanne, Lausanne, Switzerland, 5LTS5, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland
1Computational Radiology Laboratory, Boston Children's Hospital, Boston, MA, United States, 2Radiology, Harvard Medical School, Boston, MA, United States, 3Advanced Clinical Imaging Technology, Siemens Healthcare, Lausanne, Switzerland, 4Radiology, Lausanne University Hospital and University of Lausanne, Lausanne, Switzerland, 5LTS5, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland
Synopsis
Segmented 3D EPI yields higher SNR compared to conventional 2D EPI but is highly sensitive to shot-to-shot B0 variations, which result in image artifacts and compromise the achievable tSNR. In this work, we use FIDnavs combined with an augmented reconstruction strategy to compensate for the adverse effects of spatiotemporal field variations in 3D EPI. We demonstrate that FIDnavs can rapidly and accurately estimate B0 field changes up to second order in three dimensions and that FID-navigated augmented reconstruction results in improved 3D EPI image quality and temporal stability of the BOLD signal time course.
Introduction
Segmented 3D EPI yields a substantial boost in SNR efficiency compared to conventional 2D acquisitions1,2, which can be leveraged to achieve higher spatial and/or temporal resolution. This reduces partial-volume effects and signal dropout and improves statistical power in fMRI, facilitating improved localization of activation. However, as image acquisition occurs over a longer time scale (up to several seconds), 3D EPI is more sensitive to B0 fluctuations that occur due to physiological mechanisms, motion, and hardware instabilities. These shot-to-shot phase variations corrupt individual image volumes and reduce the temporal SNR (tSNR) of the BOLD time course3. In this work, we demonstrate improved 3D EPI image quality and tSNR in the presence of spatiotemporal B0 fluctuations using FID-navigated field monitoring combined with augmented reconstruction.Methods
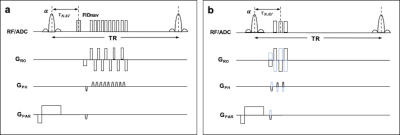
FID-navigated B0 Measurement. An FIDnav module (400 μs duration) was embedded in each repetition of a 3D EPI sequence (Fig. 1a). A forward model of the FIDnav signal was simulated using a multi-channel, low-resolution segmented 3D EPI reference image (Fig. 1b) acquired twice with reversed gradient polarities (TA~90 s). Spatiotemporal field changes were approximated using 3D spherical harmonic functions up to second order and a non-linear iterative algorithm was used to solve for B0 inhomogeneity coefficients (N=9) from the measured FIDnavs each TR4.MRI Data Acquisition. An ADNI phantom was scanned at 3T (MAGNETOM Skyra; Siemens Healthcare, Erlangen, Germany) using a 20-channel head coil. FID-navigated multi-shot EPI images (TNAV 4 ms; TE/TR 42/100 ms; FA 15°; matrix size 112x112x64; resolution 2 mm isotropic; bandwidth 812 Hz/px) were acquired with reference and modified (X+5 μT/m; Y+5 μT/m; X2-Y2+50 μT/m2) shim settings. Multi-gradient-echo (MGRE) field maps were also acquired for comparison. Raw data was combined from the two 3D EPI acquisitions (32 partition encodes per shim setting) to simulate phase variations during image encoding.
A volunteer was also scanned at 3T (MAGNETOM Prisma) following written, informed consent. Two FID-navigated multi-shot EPI images (TNAV 4 ms; TE/TR 30/89 ms; FA 20°; matrix size 112x112x44; resolution 2 mm isotropic; bandwidth 1440 Hz/px) were acquired using a 64-channel head coil in (i) a resting position and (ii) while the volunteer touched his nose. Corrupted 3D EPI images were synthesized by combining raw data from the two conditions. A whole-brain dynamic 3D EPI time series was also acquired with identical scan parameters (90 repetitions in 6 minutes) with field perturbations induced by continuous nose touching.
Image Reconstruction. The relationship between the measured k-space data $$$k$$$ and underlying image $$$\rho$$$ can be written as $$$k=E\rho$$$ where $$$E$$$ is the encoding operator. Considering the presence of susceptibility-induced geometric distortions that vary between shots, the encoding operator can be written:
$$E^i=M^iFG^i\psi^iP^i$$
where $$$P^i$$$ is a vector of phase errors corresponding to the $$$i$$$th k-space segment denoted by the mask $$$M^i$$$; $$$\psi^i$$$ is a spatial warping operator, $$$G^i$$$ is a gridding operator and $$$F$$$ is the discrete Fourier transform. The underlying image may then be estimated via a least-squares solution using iterative conjugate gradient optimization:
$$\min_{\rho}=\sum_{i}\left\| k^i-E^i\rho\right\|_2^2$$
B0 changes up to second order estimated from FIDnavs were superimposed onto the static field map, computed from MGRE images using SPM5. Image warping was performed with the NUFFT toolbox, using min-max interpolation on a 2x oversampled grid to preserve high spatial frequency components6. Data was compressed into eight virtual coils7, and augmented reconstruction was applied to each coil prior to channel combination. Normalized root-mean-square error (NRMSE) was calculated relative to the reference image. For the dynamic EPI time-series, tSNR was evaluated in the segmented brain region following rigid-body alignment in SPM for both conventional and FID-navigated augmented reconstruction.
Results
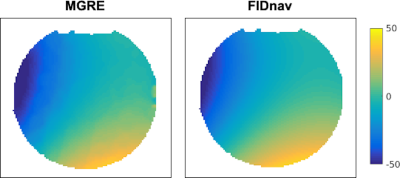
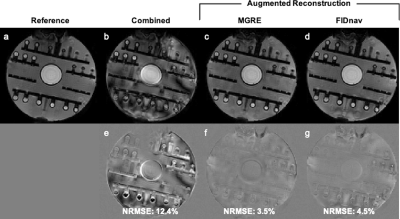
The proposed FID-navigated approach accurately estimated the applied field changes in the ADNI phantom compared to pixel-wise field maps computed from MGRE (Fig. 2). Combining data with different shim settings resulted in blurring, shading, and residual distortion artifacts in the 3D EPI image (Fig. 3b). These were mitigated by applying FID-navigated augmented reconstruction (Fig. 3d), with results comparable to augmented reconstruction using ground-truth MGRE field maps for each shim setting (Fig. 3c).Similarly, for the volunteer data (Fig. 4), combining data from two different poses resulted in substantial artifacts in the 3D EPI reconstruction (NRMSE 9.2%). These were corrected using FID-navigated augmented reconstruction (NRMSE 4.3%), which achieved highly similar results to augmenting the reconstruction with ground-truth MGRE field maps (NRMSE 4.1%).
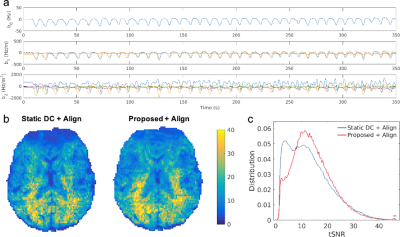
Field fluctuations measured using FIDnavs during nose touching are shown in Figure 5a. Axial tSNR maps are shown in Figure 5b for both conventional and FID-navigated augmented reconstruction. Applying the proposed method to compensate for second-order field fluctuations improved the mean tSNR within the brain by 7.2% (Fig. 5c).
Discussion
In this work, we demonstrate that FIDnavs can accurately estimate spatiotemporal B0 field changes up to second order in three dimensions. FIDnavs minimally impact the timing of the 3D EPI acquisition, enabling rapid field estimates for each shot. Combining FIDnav field monitoring with augmented reconstruction successfully mitigates artifacts that arise due to phase inconsistencies between segments in 3D EPI, facilitating a substantial improvement in tSNR. FID-navigated 3D EPI is promising for a variety of applications including high-resolution fMRI and susceptibility-weighted imaging, as well as compensating for motion-induced field changes in prospective correction.Acknowledgements
This work was supported in part by NIH grants R01 EB019483, IDDRC U54 HD090255, a pilot grant (PP-1905-34002) from the National Multiple Sclerosis Society and an Early Career Award (#14989) from the Thrasher Research Fund.References
1. Poser BA, Koopmans PJ, Witzel T, Wald LL, Barth M. Three dimensional echo-planar imaging at 7 Tesla. Neuroimage 2010;51:261–266.
2. Afacan O, Hoge WS, Janoos F, Brooks DH, Morocz IA. Rapid full-brain fMRI with an accelerated multi shot 3D EPI sequence using both UNFOLD and GRAPPA. Magn. Reson. Med. 2012;67:1266–1274.
3. van der Zwaag W, Marques JP, Kober T, Glover G, Gruetter R, Krueger G. Temporal SNR characteristics in segmented 3D-EPI at 7T. Magn. Reson. Med. 2012;67:344–352.
4. Wallace TE, Polimeni JR, Stockmann JP, Hoge WS, Kober T, Warfield SK, Afacan O. Dynamic distortion correction for functional MRI using FID navigators. Magn. Reson. Med. 2020:1–14. doi: 10.1002/mrm.28505.
5. Statistical Parametric Mapping, Wellcome Trust Centre for Neuroimaging, London, UK.
6. Sutton BP, Noll DC, Fessler JA. Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities. IEEE Trans. Med. Imaging 2003;22:178–188.
7. Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn. Reson. Med. 2013;69:571–582.
Figures
Figure 1. Pulse timing diagram showing FID-navigated 3D EPI scan (a) and reference scan (b) with reversed gradient polarities shown in blue.
Figure 2. Comparison of field difference maps (in Hz) measured from multi-gradient-echo (MGRE) data and FIDnavs for changing shim settings in the ADNI phantom. FID-navigated field estimates are in excellent agreement with ground-truth pixel-wise field maps.
Figure 3. Axial slice through 3D EPI image of ADNI phantom with reference shim settings (a), synthetic corrupted image combining data from two shim settings (b), and augmented reconstruction using ground-truth MGRE field maps (c) and FIDnav field estimates (d). Difference images relative to the reference image are also shown (e–g). Image quality is substantially improved with both ground-truth and FID-navigated augmented reconstruction.
Figure 4. Axial slice through 3D EPI image in a volunteer acquired in the reference position (a), combined image from reference position and nose touching (b), and augmented reconstruction using ground-truth MGRE field maps (c) and FIDnav field estimates (d). Difference images relative to the reference image (e–g). FID-navigated augmented reconstruction successfully compensates for artifacts in the combined image with B0 variations.
Figure 5. Zeroth-, first- and second-order B0 inhomogeneity coefficients estimated from FIDnavs during continuous nose touching (a). Axial slice through tSNR maps computed from 3D EPI scan with nose touching for conventional (static distortion correction + realignment) and the proposed FID-navigated augmented reconstruction (b). Distribution of tSNR within the whole-brain region for conventional and proposed reconstruction strategies (c). FID-navigated augmented reconstruction substantially improves tSNR of 3D EPI in the presence of spatiotemporal field fluctuations.