Introduction

In MRI fast imaging can be achieved through a combination of non-cartesian sampling trajectories, such as spirals, and iterative reconstruction techniques, such as parallel imaging (PI) and compressed sensing (CS). Drawbacks of this approach include slower convergence of the reconstruction and the appearance of artifacts induced by B₀-inhomogeneity. An efficient way to address the former issue is the use of k-space preconditioning as demonstrated by Ong et al.¹ B₀-related artifacts can be mitigated by using an expanded signal model. The latter is popularly evaluated using either time segmentation (TS) or frequency segmentation (FS), both of which lead to a high computational burden.² In this work, we investigate a fast reconstruction method, which combines the k-space preconditioned primal dual hybrid gradient method (PDHG), proposed in Ref. 1, and the B₀-aware signal model. In particular, we show how the preconditioner can be efficiently computed for this model. Moreover, we propose a generalized SVD-based approximation to more efficiently evaluate the B₀-aware imaging operator, which results in a further reduction of computation time.

Theory

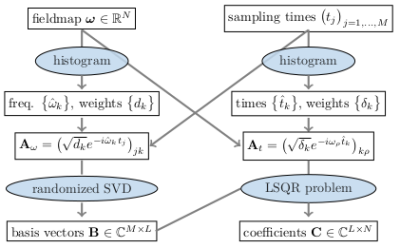
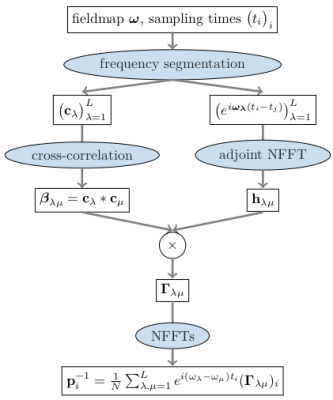
MRI reconstruction can be formulated as a convex optimization problem of the form$$\underset{\mathbf{x}}{\text{argmin}}\left\lVert{(\mathbf{F}_1\ldots\mathbf{F}_C)^T}\mathbf{x}-\mathbf{y} \right\rVert_2^2+R(\mathbf{x}),$$where $$$\mathbf{x}\in\mathbb{C}^N$$$ denotes the image to be reconstructed, $$$\mathbf{y}\in\mathbb{C}^{CM}$$$ the measured data and $$$R$$$ is a regularization term. $$$\mathbf{F}_c\in\mathbb{C}^{M\times{N}}$$$ describes the signal encoding for the c^th channel$$\big(\mathbf{F}_c\big)_{mn}=s_{cn}e^{-2{\pi}i\mathbf{k}_m\cdot\mathbf{r}_n}e^{-i\omega_n(t_m-t_E)}=s_{cn}e^{-2{\pi}i\mathbf{k}_m\cdot\mathbf{r}_n}E_{mn},$$where the matrix $$$\mathbf{E}\in\mathbb{C}^{M\times{N}}$$$ models the effect of B₀-inhomogeneity. Often this term is neglected, which leads to common artifacts, such as the blurring artifacts associated with spiral acquisitions. To efficiently evaluate the B₀-aware imaging operator, both TS and FS expand the matrix $$$\mathbf{E}$$$ using different sets of $$$L{\ll}M$$$ basis vectors chosen a priori. The evaluation of the imaging operator can then be achieved using $$$L$$$ Non-Uniform FFTs (NFFT). A problem with these approaches is the optimal choice of $$$L$$$, which can differ for different slices of a 2d acquisition depending on the field map at hand. As discussed in Ref. 2, a more optimal approach would be to compute the SVD of $$$\mathbf{E}$$$. However, this approach was not considered practical, due to the associated numerical effort. To fix this issue we propose a histogram-based strategy, which is outlined in Fig. 1. A benefit of this approach is that the appropriate number of basis functions can be estimated from the singular values of the binned matrix $$$\mathbf{A}_\omega$$$.

When using non-cartesian trajectories, a second drawback are long reconstruction times due to slow convergence of the iterative reconstruction methods. A popular method to accelerate convergence is to apply density compensation. As matter of fact, it was observed that this can increase reconstruction error.³ As an alternative, Ong propososed a fast reconstruction method, which uses the PDHG in combination with a diagonal k-space preconditioner of the form$$\underset{\mathbf{p}}{\text{argmin}}\left\lVert\text{diag}(\mathbf{p})\mathbf{FF}^H-\mathbf{1}\right\rVert_2^2,$$ where $$$\mathbf{F}$$$ denotes the encoding operator. To use this method with the B₀-aware signal model, we show that the k-space preconditioner can be computed efficiently using NFFTs, as is outlined in Fig. 2.

Methods

To test our method, we used the in-vivo brain dataset accompanying the MEDI toolbox.^4,5 The complex-valued image data was used to estimate the field map for each slice. The diagonal k-space preconditioner was computed for two variable density spiral trajectories with 3/2 interleaves and readout durations of 22/50 ms. Next k-space data was simulated for an 8 channel acquisition using the spiral with 3 interleaves and the obtained field maps. Image reconstruction was performed using $$$\ell_1$$$-regularization in the Wavelet domain. The reconstruction problem was solved using 30 iterations of PDHG both with and without diagonal k-space preconditioning. In order to evaluate the imaging operator, we used the proposed method and compared it to the TS approach with $$$L=10$$$ and $$$L=20$$$.

Results

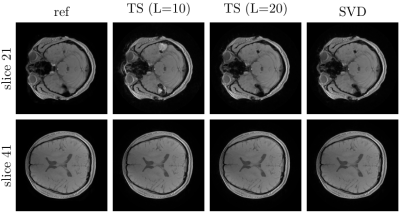
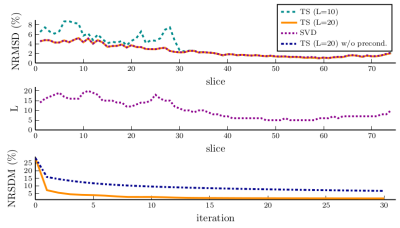
Before considering the reconstruction results, we show examples of the obtained preconditioners in Fig. 3. As can be seen the results closely match the preconditioner computed without field map information even for trajectories with long readouts. Thus, it seems reasonable to neglect the field map when computing the preconditioner in order to reduce precomputation times. The convergence plots shown in Fig. 5 illustrate the improved convergence caused by the preconditioner.

Concerning the signal model, Figs. 4 and 5 show the advantages of the proposed SVD-based approximation. As can be seen, the value of $$$L$$$ required for an artifact-free reconstruction takes on values from 6 to 20 depending on the slice. The proposed method adapts $$$L$$$ correspondingly and achieves high-quality reconstructions using $$$L=10$$$ basis functions on average. This directly translates into reduced reconstruction times due to the smaller number of NFFTs to be performed. Finally, we note that precomputation times for the SVD-based approximation were similar to those for TS.

Conclusion

This work proposes a fast method for image reconstruction of undersampled non-cartesian MRI data subject to B₀-inhomogeneity. To accelerate convergence a diagonal k-space preconditioner is used. Our results demonstrate that the latter is almost invariant with respect to B₀. Thus, it can be efficiently approximated by neglecting B₀ in its computation.

Moreover, we use a generalized SVD-based approximation to evaluate the B₀-aware imaging operator. The proposed method automatically adapts the number of basis functions to the field map at hand. As a consequence, the method helps obtaining images with low artifact level, while minimizing the reconstruction time.

Acknowledgements

No acknowledgement found.