3489
Improved Segmentation of MR Brain Images by Integrating Bayesian and Deep Learning-Based Classification1Institute for Medical Imaging Technology, School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, 2Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States
Synopsis
Accurate segmentation of brain tissues is essential for brain imaging applications. Classical Bayesian methods rely on good probability functions to produce good segmentation results. This paper presents a new method to synergistically integrate classical Bayesian segmentation with deep learning-based classification. A cluster of patch-based position-dependent neural networks were trained to effectively capture the joint spatial-intensity distributions of brain tissues. This cluster of patch networks significantly extends the capability of classical Markov Random field models and conventional statistical brain atlases. By combining the classical Bayesian classifier with the proposed networks, our method significantly improved segmentation results compared with the state-of-art methods.
Introduction
Accurate segmentation of brain tissues from MR images is essential for many brain imaging applications. While Bayesian classification-based methods1-4 and deep learning-based methods5-8 have had tremendous impact on the field over the last two decades, the accuracy of MR brain image segmentation still remains to be improved. To illustrate the problem, Fig. 1 shows a set of segmentation results obtained using the widely applied SPM segmentation tool.1 As can be seen, subtle tissue details such as cerebrospinal fluid (CSF) and white matter (WM) branches were poorly segmented. This problem was largely due to the inherent problem associated with learning the underlying high-dimensional spatial-intensity distributions of brain tissues using the classical Markov Random Field (MRF) model or its variants.2-4 Recently, deep learning-based methods have demonstrated good potentials to overcome this problem.5-8 However, large amounts of training data are needed to make such a trained network practically useful without overfitting and with good generalization capability.This paper presents a new method to synergistically integrate classical Bayesian segmentation with deep learning-based classification. The proposed method was validated using brain MR images and achieved improved segmentation compared with classical Bayesian and deep learning-based methods.
Method
The proposed method effectively utilizes the complementary strengths of Bayesian and deep learning-based classification. The overall processing pipeline is shown in Fig. 2a, which contains three integral components: a) a Bayesian classifier, b) a neural network (NN) classifier consisting of a cluster of position-dependent patch-based networks, and c) a fusion network that integrates the Bayesian and NN classification results and a statistical brain atlas.a) Bayesian classifier
The Bayesian classifier was built following the existing methods.1 The likelihood function of each tissue was modeled by a mixture of Gaussians: $$p(y_i|x_i=c,\boldsymbol{\mu}_c,\boldsymbol{\sigma}_c{,\boldsymbol{\lambda}}_c)\ =\sum_{m=1}^{M_c}{\frac{\lambda_{c_m}}{\sqrt{2\pi\sigma_{c_m}^2}}exp(-\frac{\left(y_i-\mu_{c_m}\right)^2}{2\sigma_{c_m}^2})}$$where $$$y_i$$$ and $$$x_i$$$ represent the image intensity and tissue label at the $$$i^{th}$$$ voxel respectively, and $$$\left\{{\boldsymbol{\mu}_c,\boldsymbol{\sigma}_c{,\boldsymbol{\lambda}}_c}\right\}$$$ are the model parameters, estimated from training data using the Levenberg-Marquardt algorithm.
b) Position-dependent NN classifier
Determining $$$p(x_i|\boldsymbol{y})$$$ without invoking any statistical model is computationally infeasible. To simplify the problem, we assumed $$$p(x_i|\boldsymbol{y})=p(x_i|\boldsymbol{y}_{\boldsymbol{s}_i})$$$, as is often done in classical MRF models, where $$$\boldsymbol{y}_{\boldsymbol{s}_i}$$$ is the sub-volume centered at the $$$i^{th}$$$ voxel. We then trained a cluster of position-dependent patch-based neural networks to model $$$p(x_i|\boldsymbol{y}_{\boldsymbol{s}_i})$$$ $$$(i=1,..,N)$$$ to capture the local joint spatial intensity distributions for the entire image. This cluster of patch-based networks can be viewed as a generalization of the MRF model, without imposing spatial stationarity and Gaussianity.
Specifically, we quantized the probability values of a brain atlas to $$$L$$$ levels and the collection of voxels with the same quantized probability value were treated to have the same spatial-intensity distribution and modeled by a single network. The parameters $$$\boldsymbol{\theta}$$$ of the single network $$${g(\boldsymbol{y}}_{\boldsymbol{s}_m};\boldsymbol{\theta})$$$ was optimized by minimizing the commonly used cross-entropy loss based on the training data pair $$$\left\{{{\boldsymbol{y}}_{\boldsymbol{s}_m},b_m}\right\}$$$ selected for the corresponding probability level: $$\min_{\boldsymbol{\theta}}{\left\{-\frac{1}{M}\sum_{m=1}^{M}{b_m\ log\ {g(\boldsymbol{y}}_{\boldsymbol{s}_m};\boldsymbol{\theta})\ +\ (1-b_m)\ log\ (1-log\ {g(\boldsymbol{y}}_{\boldsymbol{s}_m};\boldsymbol{\theta}))}\right\}}$$The detailed implementations of the proposed NN system are illustrated in Fig. 2b.
Compared with classical MRF models, the proposed method characterized the spatial intensity dependence with highly representative features learned without expensive training. Compared with spatial atlas that captures only spatial statistics of brain tissues across the population, the proposed method captured spatial-intensity distributions of each tissue at each point in space. Compared with existing NN classifiers that captured local spatial-intensity distributions using a single network for the entire brain, the proposed method reduced the within-class variations of the spatial-intensity distribution for each position. As a result, spatial heterogeneity of local spatial-intensity distributions was better modeled and learned.
c) Fusion network
The final classification decision was made by fusing the outputs from the Bayesian classifier, the position-dependent NN classifier and a statistical atlas. This was done by utilizing a fusion network that learns a non-linear mapping from the concatenated outputs of the individual classifier to the final decision, trained with categorical cross-entropy loss. The detailed architecture of the fusion network is shown in Fig. 2c.
Results
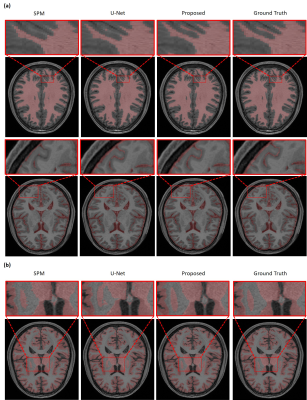
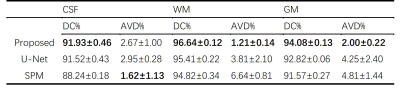
The performance of our proposed method has been evaluated using a range of in vivo brain data, especially those from the human connectome project (HCP).9 The advantages of using position-dependent patch-based networks to capture local spatial-intensity distributions are illustrated in Fig. 3, where significant improvements in tissue segmentation can be seen. A comparison of the proposed method with state-of-art methods is shown in Fig. 4. As can be seen from Fig. 4a, the CSF and WM branches were best segmented by the proposed method. Compared with the deep learning-based method, the proposed method achieved substantially improved segmentation of the deep gray matter, as shown in Fig. 4b. Table 1 shows the comparison between the proposed method and state-of-art methods quantitatively, further demonstrating the improved performance of our proposed method.Conclusions
This paper presents a new method to improve brain tissue segmentation by integrating the outputs from a Bayesian classifier, a novel NN classifier consisting of a cluster of patch-based networks, and a statistical atlas through a fusion network. The proposed method achieved improved segmentation performance of brain tissues compared with Bayesian segmentation and deep learning-based methods. The method will supplement existing methods to provide accurate segmentation of brain tissues for various brain imaging applications.Acknowledgements
No acknowledgement found.References
1. Ashburner J, Friston KJ. Unified segmentation. Neuroimage. 2005;26(3):839-851.
2. Fischl B, Salat DH, Busa E, et al. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33(3):341-355.
3. Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001;20(1):45-57.
4. Tu Z, Narr KL, Dollar P, et al. Brain anatomical structure segmentation by hybrid discriminative/generative models. IEEE Trans Med Imaging. 2008;27(4):495-508.
5. Sun L, Ma W, Ding X, et al. A 3D Spatially Weighted Network for Segmentation of Brain Tissue From MRI. IEEE Trans Med Imaging. 2020;39(4):898-909.
6. Moeskops P, Viergever MA, Mendrik AM, et al. Automatic Segmentation of MR Brain Images With a Convolutional Neural Network. IEEE Trans Med Imaging. 2016;35(5):1252-1261.
7. Dou Q, Yu L, Chen H, et al. 3D deeply supervised network for automated segmentation of volumetric medical images. Med Image Anal. 2017;41:40-54.
8. Chen H, Dou Q, Yu L, et al. VoxResNet: Deep voxelwise residual networks for brain segmentation from 3D MR images. Neuroimage. 2018;170:446-455.
9. Van Essen DC, Smith SM, Barch DM, et al. The WU-Minn Human Connectome Project: an overview. Neuroimage. 2013;80:62-79.
Figures
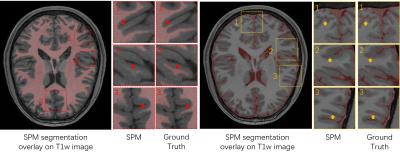
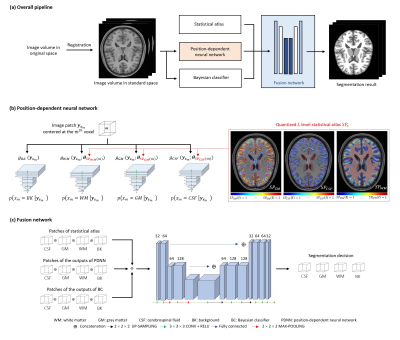
Fig. 2. Schematic of the proposed method. (a) The overall pipeline. (b) The position-dependent neural network. A large quantized probability level L would reduce the region-wise training data size, which could cause an overfitting problem, while a small L would be inadequate to characterize the heterogeneity of local spatial-intensity distributions. In the current implementation, L was empirically selected as 10. (c) The architecture of the decision level fusion network.