3439

MR Fingerprinting with B-tensor encoding scheme for simultaneous measure of relaxation and microstructure diffusion

Maryam Afzali¹, Lars Mueller¹, Ken Sakaie², Siyuan Hu³, Yong Chen⁴, Mark Griswold⁴, Derek K Jones¹, and Dan Ma³
¹Cardiff University Brain Research Imaging Centre (CUBRIC), School of Psychology, Cardiff University, Cardiff, United Kingdom, ²Imaging Institute, Cleveland Clinic, Cleveland, OH, United States, ³Biomedical Engineering, Case Western Reserve University, Cleveland, OH, United States, ⁴Radiology, Case Western Reserve University, Cleveland, OH, United States

Synopsis

Diffusion magnetic resonance imaging provides information about microstructural features of a sample. Relaxometry on the other hand is sensitive to the biochemical environment of the underlying microstructure. Recent studies show that using conventional Stejskal-Tanner experiment, separating compartmental features is challenging and therefore b-tensor encoding and diffusion-relaxometry were proposed to mitigate this challenge. Magnetic resonance fingerprinting (MRF) can quantify multiple tissue parameters in one scan. Here, we implement multi-dimensional MR Fingerprinting scan with linear and spherical tensor encoding (LTE, and STE) and show the feasibility of estimating $$$T_1,\;\rm{and}\;T_2$$$ relaxation times and diffusivity on NIST, microstructure phantom and in vivo brain scans.

Introduction

Diffusion magnetic resonance imaging (dMRI) is a powerful tool to investigate tissue microstructure ^1,2. However, disentangling the compartmental properties of the tissue is degenerate using dMRI alone, and therefore several works have suggested the combination of dMRI with relaxometry to disentangle the compartmental effects ^3-7. Recent studies also show that using the conventional Stejskal-Tanner encoding ⁸ has a fundamental drawback because the effect of isotropic diffusivity, dispersion, and microscopic anisotropy are mixed together. B-tensor encoding ⁹ was proposed to mitigate this problem and different combinations of $$$T_1$$$, $$$T_2$$$, and diffusion with and without b-tensor encoding were used in several studies ^10-16. Microscopic fractional anisotropy ($$$\mu FA$$$) that can be extracted from the combination of linear and spherical tensor encoding (LTE and STE) is a useful measure of anisotropy at the microscopic level when the conventional fractional anisotropy (FA) is not able to present the anisotropy in the underlying microstructure properly. The main challenge of in vivo applications of joint relaxometry-diffusion is the long acquisition times. Magnetic resonance fingerprinting (MRF) is a fast quantitative imaging technique that is able to quantify multiple tissue parameters simultaneously ¹⁷. In this work, we integrate free-waveform ^18,19 b-tensor diffusion encoding into the MRF framework to achieve multi-dimensional relaxation-diffusion encoding (md-MRF scan) and demonstrate the feasibility of simultaneously quantifying $$$T_1$$$, $$$T_2$$$, diffusivity, and proton density in a single scan.

Method

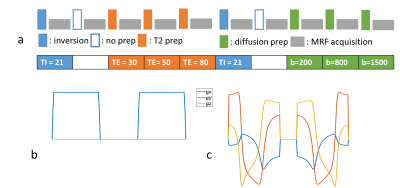
Sequence design: As shown in Figure 1, a multi-dimensional MRF (mdMRF) sequence was designed with multiple preparation modules including inversion with multiple TI times, T2 preparations with multiple TE times and diffusion preparations with multiple b-shells. After each preparation module, 48 images were acquired with varying flip angles using single-shot spiral readouts. The timings and b-values of such preparation and readout unit are listed in Figure 1a. We implemented mdMRF with linear tensor diffusion encoding (LTE) and spherical tensor diffusion encoding (STE) separately [9]. The STE gradient waveforms, shown in Figure 1c, were designed using the NOW toolbox with eddy current and concomitant field compensation [18,19]. In the mdMRF scan with LTE diffusion preparations (mdMRF-LTE), the acquisition units shown in Figure 1a was repeated multiple times with varying sampling directions. Because STE already measures isotropic diffusion, no gradient rotation was applied in the mdMRF-STE scan.
Acquisition and MRF mapping: the mdMRF-LTE and STE scans were performed on a relaxation-diffusion phantom, microstructure phantom [17] and in vivo scans on two Prisma scanners at two different institutions. For the in vivo scans, the mdMRF-LTE was acquired with 20 directions and the mdMRF-STE was acquired with one direction. The image resolution was 1.5x1.5 mm2 and 5 mm slice tickness. The scan time of the mdMRF-LTE scan was five minutes and the scan time of the mdMRF-STE scan was 50 seconds. The data from mdMRF-LTE were used to quantify $$$T_1$$$, $$$T_2$$$, ADC, FA, and proton density maps simultaneously and the data from mdMRF-STE scan was used to quantify $$$T_1$$$, $$$T_2$$$, ADC, and proton density maps.
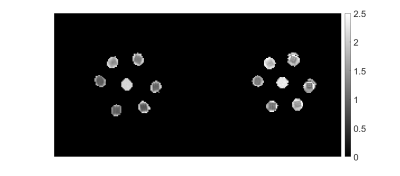
Phantom and in vivo scans: The phantom results were compared to those from conventional b-tensor diffusion scans. The microstructure phantom [20] had 6 samples where each includes one (#1, #5, #6) or two (#2, #3, #4) blocks of ~24 fibre layers (10 mm × 10 mm) inside a 15 ml centrifuge tube filled with deionized water. There was also a free water phantom in the middle labeled with number 0.
Microstructure phantom conventional diffusion scan: The microstructure phantom was scanned on a 3T Prisma MR imaging system with 80 mT/m gradients (Siemens Healthineers, Erlangen, Germany). One coronal slice with $$$1.5\times1.5\, mm^2$$$ in-plane resolution and 5 mm slice thickness and a 128128 matrix size. The acquisition protocol comprised one b=0 and 4 non-zero shells (b=200, 800, 1500, 3000 $$$s/mm^2$$$) in 20 directions per shell. We extracted some diffusion indices including mean diffusivity, fractional anisotropy, microscopic fractional anisotropy, isotropic diffusivity.

Results

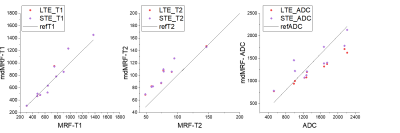
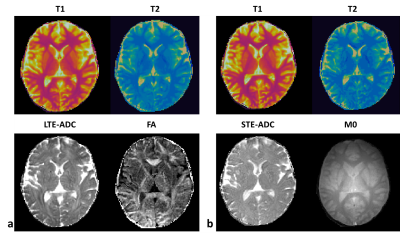
Figure 2 compares the $$$T_1$$$, $$$T_2$$$, and ADC values of a relaxation-diffusion phantom acquired from mdMRF-LTE and mdMRF-STE with those from the standard measurement. For the isotropic diffusion phantom, the $$$T_1$$$, $$$T_2$$$, and diffusivity results from mdMRF-LTE and STE are in good agreement. The $$$T_2$$$ from mdMRF scans were overestimated as compared to the measurement from a standard single echo spin-echo measurement. Figure 3 shows the $$$T_1$$$, $$$T_2$$$, ADC and FA maps from an mdMRF-LTE scan and $$$T_1$$$, $$$T_2$$$, ADC, $$$M_0$$$ maps from an mdMRF-STE scan. The results of microstructure phantom are illustrated in Figure 4. The ADC maps in the left are obtained using conventional diffusion MRI while the results in the right are from mdMRF-LTE scan. There is a good agreement between the contrast of the ADC maps from conventional MRI and the one from mdMRF-LTE scan.

Discussion and Conclusion

In conclusion, we showed the feasibility of extracting the T1, T2 relaxation times simultaneously with the apparent diffusion coefficient in the presence of b-tensor encoding in MRF. To the best of our knowledge, this is the first application of free gradient waveforms in MRF. The results of this work can be extended to clinical studies for tumor investigation where b-tensor encoding such as STE has shown promising results in non-MRF diffusion scans ¹¹.

Acknowledgements

The data were partially acquired at the UK National Facility for In Vivo MR Imaging of Human Tissue Microstructure funded by the EPSRC (grant EP/M029778/1), and The Wolfson Foundation. MA and DKJ are supported by a Wellcome Trust Investigator Award (096646/Z/11/Z) and a Wellcome Trust Strategic Award (104943/Z/14/Z). DM and SH are supported by NIH R21 EB026764 and R01 NS109439. The authors would like to thank Filip Szczepankiewicz and Markus Nilsson for providing the pulse sequences for b-tensor encoding.

References

[1] Le Bihan, Denis, et al. "MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders." Radiology 161.2 (1986): 401-407.

[2] Callaghan, Paul T., C. D. Eccles, and Y. Xia. "NMR microscopy of dynamic displacements: k-space and q-space imaging." Journal of Physics E: Scientific Instruments 21.8 (1988): 820.

[3] De Santis, Silvia, et al. "Improved precision in CHARMED assessment of white matter through sampling scheme optimization and model parsimony testing." Magnetic resonance in medicine 71.2 (2014): 661-671.

[4] Veraart, Jelle, Dmitry S. Novikov, and Els Fieremans. "TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental $$$T_2$$$ relaxation times." NeuroImage 182 (2018): 360-369.

[5] Bernin, Diana, and Daniel Topgaard. "NMR diffusion and relaxation correlation methods: New insights in heterogeneous materials." Current opinion in colloid & interface science 18.3 (2013): 166-172.

[6] Mezer, Aviv, et al. "Quantifying the local tissue volume and composition in individual brains with magnetic resonance imaging." Nature medicine 19.12 (2013): 1667-1672.

[7] de Almeida Martins, João P., and Daniel Topgaard. "Multidimensional correlation of nuclear relaxation rates and diffusion tensors for model-free investigations of heterogeneous anisotropic porous materials." Scientific Reports 8.1 (2018): 1-12.

[8] Stejskal, E. O. "Use of spin echoes in a pulsed magnetic‐field gradient to study anisotropic, restricted diffusion and flow." The Journal of Chemical Physics 43.10 (1965): 3597-3603.

[9] Westin, Carl-Fredrik, et al. "Q-space trajectory imaging for multidimensional diffusion MRI of the human brain." Neuroimage 135 (2016): 345-362.

[10] Mitra, Partha P. "Multiple wave-vector extensions of the NMR pulsed-field-gradient spin-echo diffusion measurement." Physical Review B 51.21 (1995): 15074.

[11] Szczepankiewicz, Filip, et al. "The link between diffusion MRI and tumor heterogeneity: mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE)." NeuroImage 142 (2016): 522-532.

[12] Jespersen, Sune Nørhøj. "Equivalence of double and single wave vector diffusion contrast at low diffusion weighting." NMR in Biomedicine 25.6 (2012): 813-818.

[13] Henriques, Rafael Neto, Sune N. Jespersen, and Noam Shemesh. "Microscopic anisotropy misestimation in spherical‐mean single diffusion encoding MRI." Magnetic resonance in medicine 81.5 (2019): 3245-3261.

[14] Kim, Daeun, et al. "Diffusion‐relaxation correlation spectroscopic imaging: a multidimensional approach for probing microstructure." Magnetic resonance in medicine 78.6 (2017): 2236-2249.

[15] Benjamini, Dan, and Peter J. Basser. "Magnetic resonance microdynamic imaging reveals distinct tissue microenvironments." NeuroImage 163 (2017): 183-196.

[16] Lampinen, Björn, et al. "Towards unconstrained compartment modeling in white matter using diffusion‐relaxation MRI with tensor‐valued diffusion encoding." Magnetic Resonance in Medicine 84.3 (2020): 1605-1623.

[17] Ma, Dan, et al. "Magnetic resonance fingerprinting." Nature 495.7440 (2013): 187-192.

[18] Sjölund, Jens, et al. "Constrained optimization of gradient waveforms for generalized diffusion encoding." Journal of magnetic resonance 261 (2015): 157-168.

[19] Yang, Grant, and Jennifer A. McNab. "Eddy current nulled constrained optimization of isotropic diffusion encoding gradient waveforms." Magnetic resonance in medicine 81.3 (2019): 1818-1832.

[20] Hubbard, Penny L., et al. "Biomimetic phantom for the validation of diffusion magnetic resonance imaging." Magnetic resonance in medicine 73.1 (2015): 299-305.

Figures

Figure 1: Sequence diagram of an acquisition unit of mdMRF scan. (a) Each acquisition unit consists of multiple inversion, $$$T_2$$$ and diffusion preparation modules with various timing and b-values. The table lists the key parameters of the modules. (b) and (c) are LTE and STE diffusion gradients used in the diffusion preparation modules.

Figure 2: Results of the isotropic phantom. The estimated $$$T_1$$$, $$$T_2$$$, and diffusivity values using mdMRF versus the reference values from standard measurements.

Figure 3: Estimated diffusion and relaxometry parameters. (a) $$$T_1$$$ and $$$T_2$$$ relaxation times and apparent diffusion coefficient (ADC) and fractional anisotropy (FA) from a single slice of md-MRF scan using linear tensor encoding (LTE) (b) results of md-MRF scan using spherical tensor encoding (STE). M0 shows the proton density map.

Figure 4: Estimated apparent diffusion coefficient (ADC) in $$$\mu m^2/ms$$$ from microstructure phantom using conventional linear tensor encoding (left) and the md-MRF (right).

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

3439