3438
Nonparametric 5D D-R2 distribution imaging with single-shot EPI at 21.1 T: Initial results for in vivo rat brain1National High Magnetic Field Laboratory, Florida State University, Tallahassee, FL, United States, 2Chemical and Biomedical Engineering, FAMU-FSU College of Engineering, Tallahassee, FL, United States, 3Physical Chemistry, Lund University, Lund, Sweden
Synopsis
In vivo diffusion MRI is by default performed using single-shot EPI with TE>50 ms and associated signal loss from transverse relaxation. The individual benefits of the current trends of increasing B0 to boost SNR and employing more advanced signal preparation schemes to improve the specificity for selected microstructural properties eventually may be cancelled by increases in relaxation rates at high B0 and TE with advanced encoding. Here, we make initial attempts to translate state-of-the-art diffusion-relaxation correlation methods to 21.1T to identify hurdles that need to be overcome to fulfill the promises of both high SNR and readily interpretable microstructural information.
Introduction
Advanced diffusion encoding methods (1) build on carefully crafted, but typically rather lengthy, gradient waveforms to disentangle various aspects of molecular motion, yielding improved characterization of microstructure and sub-voxel tissue heterogeneity in comparison to conventional DTI (2,3). The signal loss from transverse relaxation during the encoding waveforms could in principle be mitigated by SNR gains from using ultra-high B0 (4), which unfortunately instead often exacerbates the problems by increasing the relaxation rates (5) and image distortions from B0 inhomogeneity. While most advanced diffusion encoding studies have been performed with single-shot EPI at 3 T (6-29) or 4.7 T (30-32), there are a few recent examples at 7 T (24,33-35). As even higher fields are becoming available for in vivo human studies (4), we here perform pilot measurements with advanced diffusion encoding at the highest field available for in vivo rodent – namely 21.1 T at the National High Magnetic Field Laboratory (NHMFL) in Tallahassee, FL – to investigate the feasibility of translating pulse sequences from moderate to ultra-high fields and identify technical issues that need to be addressed. Anticipating that relaxation is the main problem, we perform measurements yielding nonparametric joint distributions of diffusion tensors D and transverse relaxation rates R2 (22,29) to individually characterize the various tissue components.Methods
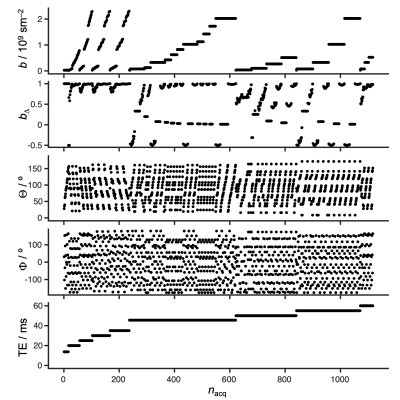
MRI was performed with a 21.1-T vertical magnet equipped with a Bruker Avance III spectrometer (Bruker-Biospin, Billerica, MA). The system is equipped with a 0.6 T/m gradient system (Resonance Research Inc., Billerca, MA), a homebuilt 33 mm quadrature surface coil (36), bite-bar, and pneumatic pillow for respiration monitoring. Anesthetized Sprague-Dawley rats (n=2) were investigated while keeping body temperature at 37 ºC and controlling respiration rate by a flow of isoflurane. Images were acquired with Paravision 6.0.1 using an EPI sequence customized for free waveform diffusion encoding (generously shared by Matthew Budde, Medical College of Wisconsin, via https://osf.io/ngu4a/#!) to achieve a 0.23x0.23 mm2 in-plane resolution, 1 mm slice thickness, 140x48x9 matrix size, and with additional acquisition parameters as reported in Figure 1. After image reconstruction in Paravision, the data was exported to Matlab (37) for denoising using random matrix theory (38), in-plane motion and eddy correction with the Matlab imregister routine, and Monte Carlo inversion (39) into nonparametric D-R2 distributions (22) using the dtr2d method in the Multidimensional diffusion MRI toolbox (40). For visualization, the axial and radial eigenvalues, DA and DR, used as primary analysis variables, were converted to the isotropic diffusivity Diso = (DA + 2DR)/3 and squared normalized anisotropy DΔ2 = (DA – DR)2/(DA + 2DR)2 (41,42).Results
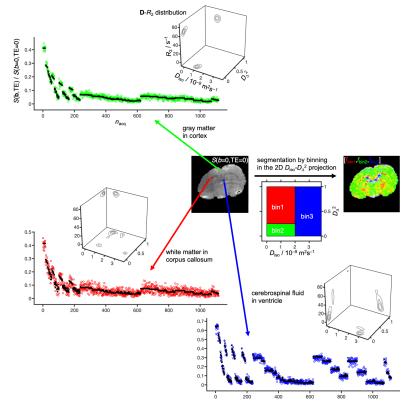
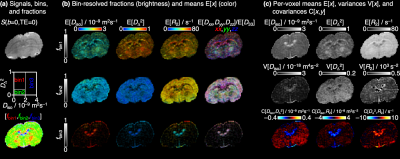
Figure 2 shows signals and corresponding D-R2 distributions for individual white matter (WM), gray matter (GM), and cerebral spinal fluid (CSF) voxels. The main components of the distributions are consistent with previous D-R2 results for in vivo human (22,29) and D-distribution data for in vivo mouse (43) – WM: low Diso, high DΔ2, and high R2; GM: low Diso, low DΔ2, and high R2; CSF: high Diso, low DΔ2, and low R2. Binning in the Diso-DΔ2 projection gives signal fraction maps roughly outlining the distribution of WM, GM, and CSF. Quantitative parameter maps derived from the per-voxel distributions are displayed in Figure 3. The bin-resolved maps reveal R2-values of 70 and 60 s–1 for, respectively, WM and GM, which can be contrasted with the values 20 and 15 s–1 observed at 3 T (22).Discussion and Cocnlusion
Reassuringly, the straightforward 21.1-T implementation of a standard EPI sequence broadly reproduces previous results from 3 T (22), however with noticeably lower image quality on account of the nearly four-fold increase in R2. To capitalize on the potential SNR gains by ultra-high field, advanced diffusion sequences may require corresponding ultra-strong gradients (28,44-46) to minimize the duration of the typically lengthy gradient waveforms, as well as image read-out with approaches such as SPEN (43,47-49) or GRASE (50) being less susceptible to B0 inhomogeneity and relaxation than single-shot EPI.Acknowledgements
This work was financially supported the Swedish Foundation for Strategic Research (ITM17-0267) and Swedish Research Council (2018-03697) to DT and the US National Institutes of Health (R01-NS102395) to SCG. DT owns shares in Random Walk Imaging AB (Lund, Sweden, http://www.rwi.se/), holding patents related to the described methods. The National High Magnetic Field Laboratory is supported by the National Science Foundation (DMR-1644779) and the State of Florida.References
1. Topgaard D, editor. Advanced Diffusion Encoding Methods in MRI. Cambridge, UK: Royal Society of Chemistry; 2020. doi: 10.1039/9781788019910
2. Basser PJ, Mattiello J, Le Bihan D. MR diffusion tensor spectroscopy and imaging. Biophys J 1994;66:259-267. doi: 10.1016/S0006-3495(94)80775-1
3. Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Di Chiro G. Diffusion tensor MR imaging of the human brain. Radiology 1996;201:637-648. doi: 10.1148/radiology.201.3.8939209
4. Le Bihan D, Schild T. Human brain MRI at 500 MHz, scientific perspectives and technological challenges. Supercond Sci Technol 2017;30:033003. doi: 10.1088/1361-6668/30/3/033003
5.Grgac K, Li W, Huang A, Qin Q, van Zijl PC. Transverse water relaxation in whole blood and erythrocytes at 3T, 7T, 9.4T, 11.7T and 16.4T; determination of intracellular hemoglobin and extracellular albumin relaxivities. Magn Reson Imaging 2017;38:234-249. doi: 10.1016/j.mri.2016.12.012
6.Avram AV, Özarslan E, Sarlls JE, Basser PJ. In vivo detection of microscopic anisotropy using quadruple pulsed-field gradient (qPFG) diffusion MRI on a clinical scanner. Neuroimage 2012;64:229-239. doi: 10.1016/j.neuroimage.2012.08.048
7.Nilsson M, Lätt J, van Westen D, Brockstedt S, Lasič S, Ståhlberg F, Topgaard D. Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging. Magn Reson Med 2013;69:1573-1581. doi: 10.1002/mrm.24395
8. Lawrenz M, Finsterbusch J. Double-wave-vector diffusion-weighted imaging reveals microscopic diffusion anisotropy in the living human brain. Magn Reson Med 2013;69:1072-1082. doi: 10.1002/mrm.24347
9. Szczepankiewicz F, Lasič S, van Westen D, Sundgren PC, Englund E, Westin C-F, Ståhlberg F, Lätt J, Topgaard D, Nilsson M. Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: Applications in healthy volunteers and in brain tumors. Neuroimage 2015;104:241-252. doi: 10.1016/j.neuroimage.2014.09.057
10.Lawrenz M, Finsterbusch J. Mapping measures of microscopic diffusion anisotropy in human brain white matter in vivo with double-wave-vector diffusion-weighted imaging. Magn Reson Med 2015;73:773-783. doi: 10.1002/mrm.25140
11.Szczepankiewicz F, van Westen D, Englund E, Westin C-F, Ståhlberg F, Lätt J, Sundgren PC, Nilsson M. The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE). Neuroimage 2016;142:522-532. doi: 10.1016/j.neuroimage.2016.07.038
12.Westin C-F, Knutsson H, Pasternak O, Szczepankiewicz F, Özarslan E, van Westen D, Mattisson C, Bogren M, O'Donnell L, Kubicki M, Topgaard D, Nilsson M. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage 2016;135:345-362. doi: 10.1016/j.neuroimage.2016.02.039
13.Lawrenz M, Brassen S, Finsterbusch J. Microscopic diffusion anisotropy in the human brain: Age-related changes. Neuroimage 2016;141:313-325. doi: 10.1016/j.neuroimage.2016.07.031
14. Lampinen B, Szczepankiewicz F, Mårtensson J, van Westen D, Sundgren PC, Nilsson M. Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: A model comparison using spherical tensor encoding. Neuroimage 2017;147:517-531. doi: 10.1016/j.neuroimage.2016.11.053
15.Lampinen B, Szczepankiewicz F, van Westen D, Englund E, Sundgren PC, Lätt J, Ståhlberg F, Nilsson M. Optimal experimental design for filter exchange imaging: Apparent exchange rate measurements in the healthy brain and in intracranial tumors. Magn Reson Med 2017;77:1104-1114. doi: 10.1002/mrm.26195
16.Yang G, Tian Q, Leuze C, Wintermark M, McNab JA. Double diffusion encoding MRI for the clinic. Magn Reson Med 2018;80:507-520. doi: 10.1002/mrm.27043
17. Avram AV, Sarlls JE, Basser PJ. Measuring non-parametric distributions of intravoxel mean diffusivities using a clinical MRI scanner. Neuroimage 2019;185:255-262. doi: 10.1016/j.neuroimage.2018.10.030
18. Lampinen B, Szczepankiewicz F, Novén M, van Westen D, Hansson O, Englund E, Mårtensson J, Westin CF, Nilsson M. Searching for the neurite density with diffusion MRI: Challenges for biophysical modeling. Hum Brain Mapp 2019;40:2529-2545. doi: 10.1002/hbm.24542
19.Lawrenz M, Finsterbusch J. Detection of microscopic diffusion anisotropy in human cortical gray matter in vivo with double diffusion encoding. Magn Reson Med 2019;81:1296-1306. doi: 10.1002/mrm.27451
20. Nery F, Szczepankiewicz F, Kerkela L, Hall MG, Kaden E, Gordon I, Thomas DL, Clark CA. In vivo demonstration of microscopic anisotropy in the human kidney using multidimensional diffusion MRI. Magn Reson Med 2019;82:2160-2168. doi: 10.1002/mrm.27869
21. Yang G, McNab JA. Eddy current nulled constrained optimization of isotropic diffusion encoding gradient waveforms. Magn Reson Med 2019;81:1818-1832. doi: 10.1002/mrm.27539
22. de Almeida Martins JP, Tax CMW, Szczepankiewicz F, Jones DK, Westin C-F, Topgaard D. Transferring principles of solid-state and Laplace NMR to the field of in vivo brain MRI. Magn Reson 2020;1:27-43. doi: 10.5194/mr-1-27-2020
23.Lampinen B, Szczepankiewicz F, Mårtensson J, van Westen D, Hansson O, Westin C-F, Nilsson M. Towards unconstrained compartment modeling in white matter using diffusion-relaxation MRI with tensor-valued diffusion encoding. Magn Reson Med 2020;84:1605-1623. doi: 10.1002/mrm.28216
24. Lampinen B, Zampeli A, Björkman-Burtscher IM, Szczepankiewicz F, Kallen K, Compagno Strandberg M, Nilsson M. Tensor-valued diffusion MRI differentiates cortex and white matter in malformations of cortical development associated with epilepsy. Epilepsia 2020. doi: 10.1111/epi.16605
25. Nilsson M, Szczepankiewicz F, Brabec J, Taylor M, Westin CF, Golby A, van Westen D, Sundgren PC. Tensor-valued diffusion MRI in under 3 minutes: an initial survey of microscopic anisotropy and tissue heterogeneity in intracranial tumors. Magn Reson Med 2020;83:608-620. doi: 10.1002/mrm.27959
26. Andersen KW, Lasič S, Lundell H, Nilsson M, Topgaard D, Sellebjerg F, Szczepankiewicz F, Siebner HR, Blinkenberg M, Dyrby TB. Disentangling white-matter damage from physiological fiber orientation dispersion in multiple sclerosis. Brain Commun 2020;2:fcaa077. doi: 10.1093/braincomms/fcaa077
27. Reymbaut A, Critchley J, Durighel G, Sprenger T, Sughrue M, Bryskhe K, Topgaard D. Towards non-parametric diffusion-T1 characterization of crossing fibers in the human brain. Magn Reson Med 2020;Accepted. doi: 10.1002/mrm.28604
28.Tan ET, Shih RY, Mitra J, Sprenger T, Hua Y, Bhushan C, Bernstein MA, McNab JA, DeMarco JK, Ho VB, Foo TKF. Oscillating diffusion-encoding with a high gradient-amplitude and high slew-rate head-only gradient for human brain imaging. Magn Reson Med 2020;84:950-965. doi: 10.1002/mrm.28180
29. de Almeida Martins JP, Tax CMW, Reymbaut A, Szczepankiewicz F, Chamberland M, Jones DK, Topgaard D. Computing and visualising intra-voxel orientation-specific relaxation-diffusion features in the human brain. Hum Brain Mapp 2020;Accepted. doi: 10.1002/hbm.25224
30.Baron CA, Beaulieu C. Oscillating gradient spin-echo (OGSE) diffusion tensor imaging of the human brain. Magn Reson Med 2014;72:726-736. doi: 10.1002/mrm.24987
31.Baron CA, Kate M, Gioia L, Butcher K, Emery D, Budde M, Beaulieu C. Reduction of diffusion-weighted imaging contrast of acute ischemic stroke at short diffusion times. Stroke 2015;46:2136-2141. doi: 10.1161/STROKEAHA.115.008815
32. Tetreault P, Harkins KD, Baron CA, Stobbe R, Does MD, Beaulieu C. Diffusion time dependency along the human corpus callosum and exploration of age and sex differences as assessed by oscillating gradient spin-echo diffusion tensor imaging. Neuroimage 2020;210:116533. doi: 10.1016/j.neuroimage.2020.116533
33. Maximov, II, Vellmer S. Isotropically weighted intravoxel incoherent motion brain imaging at 7T. Magn Reson Imaging 2019;57:124-132. doi: 10.1016/j.mri.2018.11.007
34.Szczepankiewicz F, Sjölund J, Ståhlberg F, Lätt J, Nilsson M. Tensor-valued diffusion encoding for diffusional variance decomposition (DIVIDE): Technical feasibility in clinical MRI systems. PLOS One 2019;14:e0214238. doi: 10.1371/journal.pone.0214238
35. Arbabi A, Kai J, Khan AR, Baron CA. Diffusion dispersion imaging: Mapping oscillating gradient spin-echo frequency dependence in the human brain. Magn Reson Med 2020;83:2197-2208. doi: 10.1002/mrm.28083
36. Rosenberg, J.T.; Shemesh, N.; Muniz, J.A.; Dumez, J.N.; Frydman, L.Grant, S.C., Transverse relaxation of selectively excited metabolites in stroke at 21.1 T. Magnet. Reson. Med., 2017:77 (2)
37. Matlab R2018b. Natick, MA: The MathWorks.
38.Veraart J, Fieremans E, Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magn Reson Med 2016;76:1582-1593. doi: 10.1002/mrm.26059
39.Prange M, Song YQ. Quantifying uncertainty in NMR T2 spectra using Monte Carlo inversion. J Magn Reson 2009;196:54-60. doi: 10.1016/j.jmr.2008.10.008
40. Nilsson M, Szczepankiewicz F, Lampinen B, Ahlgren A, de Almeida Martins JP, Lasič S, Westin C-F, Topgaard D. An open-source framework for analysis of multidimensional diffusion MRI data implemented in MATLAB. Proc Intl Soc Mag Reson Med 2018;26:5355.
41. Conturo TE, McKinstry RC, Akbudak E, Robinson BH. Encoding of anisotropic diffusion with tetrahedral gradients: A general mathematical diffusion formalism and experimental results. Magn Reson Med 1996;35:399-412. doi: 10.1002/mrm.1910350319
42. Eriksson S, Lasič S, Nilsson M, Westin C-F, Topgaard D. NMR diffusion encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. J Chem Phys 2015;142:104201. doi: 10.1063/1.4913502
43. Yon M, de Almeida Martins JP, Bao Q, Budde MD, Frydman L, Topgaard D. Diffusion tensor distribution imaging of an in vivo mouse brain at ultra-high magnetic field by spatiotemporal encoding. NMR Biomed 2020;33:e4355. doi: 10.1002/nbm.4355
44. Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, Keil B, Tisdall MD, Hoecht P, Dietz P, Cauley SF, Tountcheva V, Matschl V, Lenz VH, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D, Rosen BR, Wedeen V, Wald LL. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage 2013;80:220-233. doi: 10.1016/j.neuroimage.2013.05.078
45. Jones DK, Alexander DC, Bowtell R, Cercignani M, Dell'Acqua F, McHugh DJ, Miller KL, Palombo M, Parker GJM, Rudrapatna US, Tax CMW. Microstructural imaging of the human brain with a 'super-scanner': 10 key advantages of ultra-strong gradients for diffusion MRI. Neuroimage 2018;182:8-38. doi: 10.1016/j.neuroimage.2018.05.047
46. Hennel F, Michael ES, Pruessmann KP. Improved gradient waveforms for oscillating gradient spin-echo (OGSE) diffusion tensor imaging. NMR Biomed 2020:e4434. doi: 10.1002/nbm.4434
47. Leftin A, Rosenberg JT, Solomon E, Calixto Bejarano F, Grant SC, Frydman L. Ultrafast in vivo diffusion imaging of stroke at 21.1 T by spatiotemporal encoding. Magn Reson Med 2015;73:1483-1489. doi: 10.1002/mrm.25271
48.Solomon E, Liberman G, Nissan N, Frydman L. Robust diffusion tensor imaging by spatiotemporal encoding: Principles and in vivo demonstrations. Magn Reson Med 2017;77:1124-1133. doi: 10.1002/mrm.26197
49. Leftin A, Rosenberg JT, Yuan X, Ma T, Grant SC, Frydman L. Multiparametric classification of sub-acute ischemic stroke recovery with ultrafast diffusion, 23Na, and MPIO-labeled stem cell MRI at 21.1 T. NMR Biomed 2020;33:e4186. doi: 10.1002/nbm.4186 50. Wu D, Liu D, Hsu Y-C, Li H, Sun Y, Qin Q, Zhang Y. Diffusion-prepared 3D gradient spin-echo sequence for improved oscillating gradient diffusion MRI. Magn Reson Med 2021;85:78-88. doi: 10.1002/mrm.28401
51. Basser PJ, Mattiello J, Le Bihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B 1994;103:247-254. doi: 10.1006/jmrb.1994.1037
Figures