Introduction

Microstructural imaging is used to quantify tissue properties using multi-shell diffusion imaging techniques^1,2,3,4. Tissue can be modeled as three or two compartments: intra-axonal and extra-axonal (and free). Using multi-shell or diffusion spectrum imaging-based sampling, DW-MRI can be used to characterize the microarchitecture of biological tissue like white matter using popular diffusion modeling methods like CHARMED³, NODDI², and SMT¹.

NODDI², SMT¹, and similar methods assume the same T₂ decay for each compartment and can be truncated from the mathematical model by normalizing DWIs with non-diffusion MRI (b=0). Recently Veraart⁴ et al proposed a framework, TEdDI⁴, that can model T₂, volume fraction, and axial/radial diffusivities for intra/extra-axonal compartment. Although TEdDI⁴ is a very comprehensive model with the caveat of requiring a scanning protocol with multiple sets of multi-shell diffusion imaging dataset varying echo-time for each set.

We propose a novel modeling framework that extends SMT¹ to estimate T₂ for Intra/extra-axonal compartments. Simultaneously, we also propose a numerical framework to estimate T2 for extra/intra-axonal compartments that utilize a typical multi-shell diffusion MRI protocol. The proposed method requires a different minimum of echo-time for each shell.

Method

Data acquisition: A healthy 38-year-old male was scanned on 3T Siemens TrioTim magnet with b=1000 s/mm² and b=3000 s/mm² with 64 gradient directions and b=5000 s/mm² with 128 gradient directions along with b=0 images for every 10 of diffusion-weighted images with a total acquisition time of 17 minutes. Other MR parameters are as follows; FoV 230.4x230.4 mm: voxel size: 2.4x2.4x2.4mm³ with 63 axial slices. Minimum TE is chosen for each shell is chosen to be minimum, 92ms, 125ms, and 147ms for b=1000, 3000, and 5000 shells respectively.
Preprocessing: Each diffusion shell was preprocessed separately and then registered together using b=0 images from each shell. Denoising⁸, unring⁹, N4 bias correction¹², eddy¹⁰, and topup¹¹ correction were performed using mrtrix, FSL⁶, and ANTS¹² software packages. Preprocessed data was utilized to estimate the powered average for each shell. The mean value of DWIs was calculated using mrtrix and further used in SMT¹ based formulation. Scipy’s curve_fit function is used to optimize for non-linear fitting for each voxel.

Formulation: We have used SMT¹ to fit the estimated powered average MR signal for each that is dependent on b-value and TE. TE-dependent SMT model is described in the following equation:
$$\overline{S}(TE,b)=\rho[{\ f}_{in}{\ e}^{-\ \frac{TE}{T_2^{in}}}\ \psi(\ b\lambda\ )\ +\ {(1.0\ -\ f}_{in})\ {\ e}^{-\ \frac{TE}{T_2^{ex}}}\psi(\ bf_{in}\lambda)\ ]$$
where $$$ \psi(\ x)\ =\sqrt\pi\ erf(\sqrt x)/2x $$$ with $$${\lambda\ =\lambda}_\parallel=(1.0\ -\ f_{in})\ \lambda_\bot$$$ and $$$T_2^{in}$$$ and $$$T_2^{ex}$$$ are T₂ values for intra/extra-axonal compartment. $$$f_{in}$$$ is the volume fraction for the intracellular compartment. $$$ \lambda_\parallel$$$ and $$$\lambda_\bot$$$are axial and radial diffusivity for intra/extra-axonal compartment respectively. The tortuosity condition is used for the final equation.
Numerical Optimization: Equation can be solved as a non-linear constrained optimization problem with four parameters {$$$f_{in}$$$, $$$\lambda$$$, $$$T_2^{in}$$$ and $$$T_2^{ex}$$$ }. It is an ill-posed problem and can have multiple local minima and hence does not converge optimally under all scenarios. To find an optimal solution, we first find an approximate solution, that can be used as an initial guess and then the interval around the approximate solution can be used as constrained to nonlinear optimization.
Here are steps for estimating an approximate solution:

1. Estimate proton density,$$$\rho$$$ , for b=0 by assuming, $$$T_2^{in}\approx T_2^{ex}\approx T_2$$$,

$$\overline{S}(TE,\ b=0)=\rho e^{-\frac{TE}{T_2}}$$
2. Estimate $$$f_{in}$$$ and $$$\lambda$$$ using the following equation:
$$ \frac{\overline{S}(TE,\ b)}{\overline{S}(TE,\ b=0)}=[{\ f}_{in}\ \psi(\ b\lambda\ )\ +\ {(1.0\ -\ f}_{in})\ \psi(\ bf_{in}\lambda)\ ]$$
3. For large b-value, $$$b_{l} \approx 5000$$$ s/mm², the extracellular compartment signal can be negligible⁵, and the equation1 can be reduced to one-compartment model and can be solved for $$$T^{in}_{2}$$$ using an estimated value for $$$\rho$$$, $$$f_{in}$$$ and $$$\lambda$$$,
$$ T_2^{in}=\frac{TE}{ln\left(\frac{{\ f}_{in}\ \psi(b_l\ \lambda)}{\frac{\overline{S}(TE,\ b_l)}{\rho}}\right)}$$
4. For small b-value, $$$b_{s} \approx 1000$$$ s/mm², we can estimate $$$T_2^{ex}$$$ by substituting values estimated in steps 1-3.
$$ T_2^{ex}=\frac{TE}{ln\left(\frac{{(1.0\ -\ f}_{in})\ \psi(b_s\ \lambda{\ f}_{in})}{\frac{\overline{S}(TE,\ b_s)}{\rho}\ -\ {\ f}_{in}e^{-\frac{TE}{T_2^{in}}}\ \psi(\ b_s\lambda\ )}\right)}$$
Using the estimated values for $$$f_{in}$$$ and $$$\lambda$$$, $$$T_2^{in}$$$ and $$$T_2^{ex}$$$ as initial guess and interval around it (±30% for T₂ and ±10% for $$$f_{in}$$$ and $$$\lambda$$$) as constraint, we can solve equation using linear least squares or Levenberg-Marquardt algorithm depending upon constraints. This was implemented using scipy’s curve_fit function.

Results and Discussion

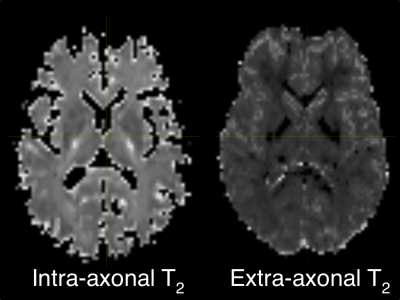
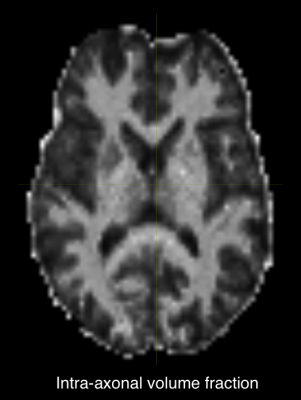
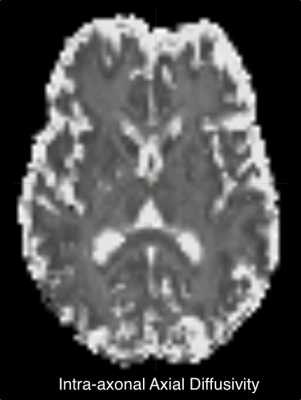
Fig.1 shows an axial slice of T₂ values for intra/extra-axonal compartments. This slice looks similar to the estimated T₂ in [1]. Intra-axonal T₂ in the internal capsule shows high values which suggested highly myelinated axons in those regions. We report estimated average T2 for all white matter ROIs in the whole brain.
Fig.2 shows the axial slice for the intra-axonal volume fraction. This shows a clear segmentation of white matter similar to typical SMT¹ fit. Similarly, intra/extra-axonal diffusivity maps are shown in (Fig.3) indicating the expected values for each tissue type.

Conclusion

We have proposed an extended SMT framework to estimate intra/extra-axonal T₂ along with volume fraction and axial and radial diffusivity. A novel numerical framework is also presented to estimate all parameters for a typical multi-shell diffusion protocol. T₂ for Intra/extra-axonal compartment can be a potential biomarker for diseases like multiple-sclerosis or Alzheimer’s disease. In future studies will explore compartment T₂ of brain-tissue damage in TBI-population.