3433
Physically Motivated Deep-Neural Networks of the Intravoxel Incoherent Motion Signal Decay Model for Quantitative Diffusion-Weighted MRI1Biomedical Engineering, Technion, Haifa, Israel, 2Boston's Children's Hospital, Harvard Medical School, Boston, MA, United States
Synopsis
Quantitative Diffusion-Weighted MRI with the Intra-Voxel Incoherent Motion (IVIM) model shows potential to produce quantitative biomarkers for multiple clinical applications. Recently, deep-learning (DL) models were proposed for the estimation of the IVIM model parameters from DW-MRI data. While the DL models produce more accurate parameter estimates compared to classical methods, their capability to generalize the IVIM model to different acquisition protocols is very limited. For that end, we introduce a physically motivated DL model, by incorporating the acquisition protocol into the network architecture. Our approach provides a DL-based method for IVIM parameter estimates that is agnostic to the acquisition protocol.
Introduction
Body Diffusion-weighted MRI (DW-MRI) has the potential to enable detailed characterization of the tissue cellular architecture due to its sensitivity to the random movement of individual water molecules [1]. According to the Intra-Voxel Incoherent Motion (IVIM) model, the overall MRI attenuation may be expressed as the a bi-exponential decay [2] related to the diffusion and pseudo-diffusion components:si=s0(Fpexp(-bi(Dp+D))+(1-Fp)exp(-biDp)) , (1)
where si is the signal at b-value bi; s0 is the signal without sensitizing the diffusion gradients; D is the diffusion coefficient, an indirect measure of tissue cellularity; Dp is the pseudo-diffusion coefficient, an indirect measure of blood flow in the micro-capillaries network; and Fp is the fraction of the contribution of the pseudo-diffusion to the signal decay. The IVIM model parameters have recently been shown to serve as promising quantitative imaging biomarkers for various clinical applications, such as tumor analysis [3], [4] assessment of liver cirrhosis [5] and Crohn’s disease [6], [7]. However, obtaining voxel-wise IVIM parameter estimates from DW-MRI data with the classical non-linear least-squares (NLLS) regression approach [8] results in noisy and unreliable parameter estimates due to the non-linearity of the IVIM model and low signal-to-noise ratio (SNR) observed in body DW-MRI [9]. In addition, Bayesian approaches, such as the Bayesian Shrinkage Prior (BSP) [10] and the Fusion Bootstrap Moves (FBM) [11], are computational expensive and highly sensitive to the choice of prior distributions. Recently, the use of deep-neural-networks (DNNs) has been proposed for IVIM parameter estimation by Bertleff [12] and Barbieri [13]. While these DNN-based approaches show improved performance in terms of accuracy and computational time, they fail in predicting the IVIM model parameters from DW-MRI data acquired with a set of b-values that was not used during the DNN training. This limits their practical usage in clinical settings, where variations in the acquisition protocol are common. In this work, we introduce an improved DNN-based model for the IVIM signal decay by incorporating the DW-MRI acquisition parameters into the DNN architecture input in addition to the attenuated signals.
Methods
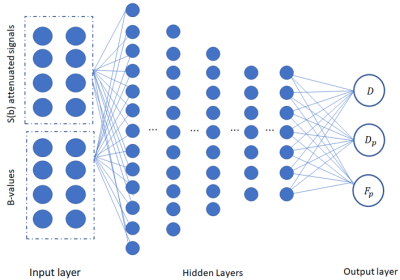
A feed-forward back-propagation deep neural network was trained using data generated according to the IVIM model (Eq. 1). The network is comprised of five fully-connected hidden layers, an extended input layer and an output layer (see Fig. 1). The input layer is composed of the neurons which receive the normalized diffusion-weighted signals , as well as the values of the acquisition parameters. The output layer is comprised of 3 neurons, which hold the estimations of the IVIM model parameters: D, Dp and Fp . An Adam optimizer was applied for the training, with a loss function computed as the mean square error between the normalized signal input and the normalized predicted output according to the IVIM model (Eq. (1)). The proposed network was trained and tested on simulated diffusion-weighted signals, according to the IVIM model, with randomly varying b-values vectors. The IVIM parameters were chosen as uniformly distributed random variables over the following intervals: 0.0005≤D≤0.002 mm2/sec, 0.01≤Dp≤0.1 mm2/sec, 0.1≤Fp≤0.4. These parameters values were chosen in agreement with reported abdominal DW-MRI data [14]. During the training process, uniformly distributed random variations in the b-values vectors were injected to the network. Rician noise was added to the IVIM signals during the training process.Results
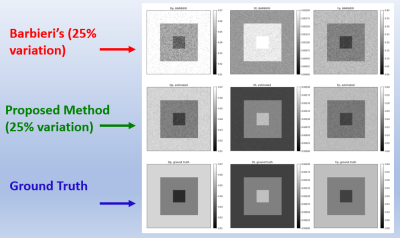
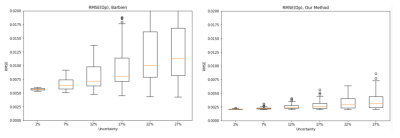
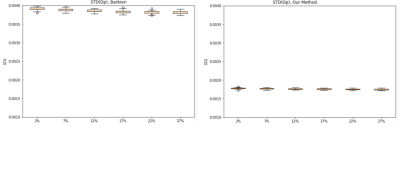
The proposed deep neural network was successfully trained for the IVIM model, with a b-values variability bias of 25%. In Fig. 2, an example of the proposed method’s parameter estimations compared to Barbieri’s method is shown. The proposed method achieves improved estimations of the IVIM parameters with respect to the ground truth (GT) data, compared to previous network estimations. In Fig. 3, the Root-Mean-Square-Error (RMSE) of the IVIM parameters over different tested parameters variability is shown, for Barbieri’s and the proposed method. As may be seen, the proposed method achieves improved RMSEs for the DP estimations compared to Barbieri’s method over the tested parameters variabilities. Similar results are obtained for D, Fp. In Fig. 4, box plots for the standard deviations (STDs) of the estimated parameters maps are shown for different parameter variations, where for each variation, Rician noise is generated and added to the IVIM signal over 100 iterations. The STDs are calculated over uniform areas in the parameters’ maps, in order to demonstrate the sensitivity of the two compared methods for the Rician noise. As may be seen, the proposed method achieves lower STDs for all tested variations, for the Dp estimate. Similar results are obtained for D, Fp.Conclusions
We introduced a deep learning model capable to “learn” the IVIM signal model decay by incorporating the acquisition parameters into the network architecture. In a major shift from previous work, which focused on accurate prediction of the IVIM model parameters in a specific setting (i.e., a set of b-values), our approach is capable to “learn” the IVIM model and as a result, be agnostic to variations in the acquisition protocols. Thus, the proposed DNN-based model of the IVIM signal-decay model may be used to estimate the IVIM model parameters from DW-MRI data, without requiring an additional training session according to the specific acquisition protocol parameters. The proposed approach can be extended directly to additional parametric MRI quantitative mappings.Acknowledgements
This research was supported in part by a grant from the United States-Israel Binational Science Foundation (BSF), Jerusalem, IsraelReferences
[1] D. M. Koh and D. J. Collins, “Diffusion-weighted MRI in the body: Applications and challenges in oncology,” Am. J. Roentgenol., vol. 188, no. 6, pp. 1622–1635, 2007.
[2] D. Le Bihan, E. Breton, D. Lallemand, M. L. Aubin, J. Vignaud, and M. Laval-Jeantet, “Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging,” Radiology, vol. 168, no. 2, pp. 497–505, 1988.
[3] C. Federau, R. Meuli, K. O’Brien, P. Maeder, and P. Hagmann, “Perfusion measurement in brain gliomas with intravoxel incoherent motion MRI,” Am. J. Neuroradiol., vol. 35, no. 2, pp. 256–262, 2014.
[4] H. Chandarana et al., “Diffusion-weighted intravoxel incoherent motion imaging of renal tumors with histopathologic correlation,” Invest. Radiol., vol. 47, no. 12, pp. 688–696, 2012.
[5] A. M. Chow et al., “Liver fibrosis: An intravoxel incoherent motion (IVIM) study,” J. Magn. Reson. Imaging, vol. 36, no. 1, pp. 159–167, 2012.
[6] M. Freiman et al., “Characterization of fast and slow diffusion from diffusion-weighted MRI of pediatric Crohn’s disease,” J. Magn. Reson. Imaging, vol. 37, no. 1, pp. 156–163, 2013.
[7] S. J. Hectors et al., “Diffusion and perfusion MRI quantification in ileal Crohn’s disease,” Eur. Radiol., vol. 29, no. 2, pp. 993–1002, 2019.
[8] H. Merisaari et al., “Fitting methods for intravoxel incoherent motion imaging of prostate cancer on region of interest level: Repeatability and gleason score prediction,” Magn. Reson. Med., vol. 77, no. 3, pp. 1249–1264, 2017.
[9] M. Iima and D. Le Bihan, “Clinical intravoxel incoherent motion and diffusion MR imaging: Past, present, and future,” Radiology, vol. 278, no. 1. pp. 13–32, 2016.
[10] M. R. Orton, D. J. Collins, D. M. Koh, and M. O. Leach, “Improved intravoxel incoherent motion analysis of diffusion weighted imaging by data driven Bayesian modeling,” Magn. Reson. Med., 2014. [11] M. Freiman et al., “Reliable estimation of incoherent motion parametric maps from diffusion-weighted MRI using fusion bootstrap moves,” Med. Image Anal., vol. 17, no. 3, pp. 325–336, 2013.
[12] M. Bertleff et al., “Diffusion parameter mapping with the combined intravoxel incoherent motion and kurtosis model using artificial neural networks at 3 T,” NMR Biomed., vol. 30, no. 12, 2017.
[13] S. Barbieri, O. J. Gurney-Champion, R. Klaassen, and H. C. Thoeny, “Deep learning how to fit an intravoxel incoherent motion model to diffusion-weighted MRI,” Magn. Reson. Med., vol. 83, no. 1, pp. 312–321, 2020.
[14] V. Taimouri et al., “Spatially constrained incoherent motion method improves diffusion-weighted MRI signal decay analysis in the liver and spleen.,” Med. Phys., vol. 42, no. 4, p. 1895, 2015.
Figures