Introduction

Diffusion tensor imaging (DTI) and intravoxel incoherent motion (IVIM) yield detailed information about tissue microstructure and can improve our understanding of the pathophysiology of several diseases^1,2. In well-perfused organs with ordered microstructure, such as the kidneys, a combination of both DTI and IVIM is desirable. However, conventional IVIM, DTI and the combination of both face some challenges: (1.) Protocols suffer from long acquisition times due to the need for many b-values and/or diffusion directions; (2.) Fits from noisy (diffusion-weighted) images result in noisy parameter maps; (3.) Rician noise introduces a noise-dependent bias in parameter values.

Model-based reconstruction has the potential to overcome these shortcomings. It facilitates parameter estimation directly from k-space by combining the model and the MRI signal generation in the reconstruction process. Higher undersampling factors can be obtained while simultaneously preserving image quality^3–5. Furthermore, as noise is Gaussian in k-space, no systematic noise-bias is introduced.

The aim of this work was to assess the feasibility of model-based reconstructions for pure IVIM and combined IVIM-DTI fitting in well-perfused abdominal organs.

Methods

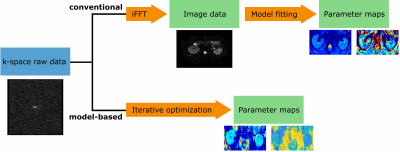
All scans were performed with a 3T MRI (Philips Ingenia, Best, The Netherlands) on healthy participants. Raw and image data were exported. Liver data was acquired in three volunteers, kidney data in two. Diffusion-weighted EPI scan parameters were as followed: Liver scan in free-breathing, TE/TR=63ms/7000ms, 27 slices, 3x3x6mm³ (1 volunteer: 3x3x5mm³), 1mm slice gap, SENSE factor 2, 18 b-values (range 0-700s/mm²), 3 diffusion directions each, 9 b=0s/mm² scans. Kidneys: navigator-triggered scan, 15-18 slices to cover whole kidneys, 2.5x2.5x5mm³ resolution, 0.3mm slices gap, SENSE factor 2, TE/TR=62ms/982ms, 10 b-values (range 0-600s/mm²), 32 diffusion directions for high b-values (200-400s/mm²), 6 directions for lower b-values, 16 b=0s/mm² scans.

Model-based reconstruction was performed on the raw data using the PyQMRI Toolbox⁶ written in Python after applying basic corrections. An IVIM and IVIM-DTI model were implemented. PyQMRI uses an iteratively regularized Gauss-Newton approach with total generalized variation regularization⁷. In this work 7 Gauss-Newton iterations were used. An illustration of the conventional fitting and model-based reconstruction process is shown in Figure 1.

For comparison the image data obtained from the scanner was fitted voxel-wise to an IVIM or IVIM-DTI model in Python using the DiPy⁸ toolbox. The IVIM-DTI fit was performed in two steps: first, the IVIM fit was performed, yielding the perfusion fraction f and pseudo-diffusion coefficient D*; then the perfusion component was subtracted from the signal and the diffusion tensor was fitted to the remaining signal. The liver data was fitted to a pure IVIM model:
$$S(b)=S_0\cdot(f\cdot e^{-bD^{*}}+(1-f)\cdot e^{-bD})$$
S(b) denotes the signal at given b-value b, S₀ is the signal at b=0s/mm², D is the diffusion coefficient, D* pseudo-diffusion coefficient and f perfusion fraction. Kidney data was fitted to a combined IVIM-DTI model with diffusion tensor $$$\underline{\underline{D}}$$$ and diffusion gradient orientations $$$\underline{g}$$$:
$$S(b)=S_0\cdot(f\cdot e^{-bD^{*}}+(1-f)\cdot e^{-\underline{g}^{T}\underline{\underline{D}}\underline{g}})$$
From the diffusion tensor the mean diffusivity (MD) and fractional anisotropy (FA) were calculated. Regions of interest (ROIs) were drawn on the DiPy output S₀ maps in all slices covering the liver or kidney. ROIs of the kidney were drawn in the cortex only. Outcome measures are shown as mean values and standard deviation over the full segmented volume.

Results

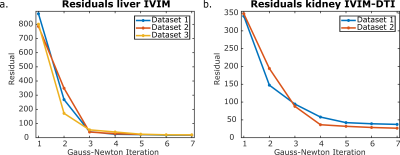
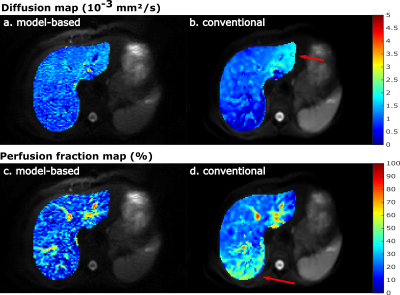
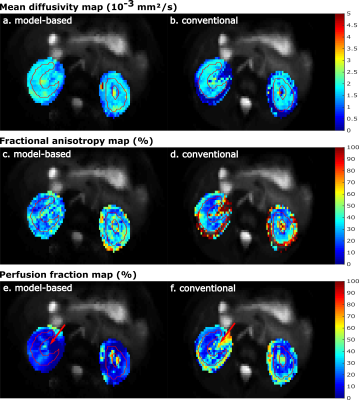
Figure 2 shows the value of the cost function after each Gauss-Newton iteration for the IVIM and IVIM-DTI model. The largest decrease of the residuals was observed in the first three iterations for each dataset and model. After five iterations the cost function reached a plateau and more iterations did not further decrease the residuals substantially.

Representative parameter maps are shown in Figure 3 for the liver and Figure 4 for the kidneys. The liver maps obtained from the conventional fit had a smooth appearance, but displayed abnormal regional heterogeneity, such as a high perfusion anterior and high D in the left liver lobe – a known artefact from cardiac motion. The model-based reconstructions seems to be unaffected by these unexpected heterogeneities. For the kidneys, the model-based reconstructions yielded consistent parameter maps, which revealed more anatomical detail than those obtained with conventional fitting. This was particularly observed in the perfusion map (Figures 4e and 4f).

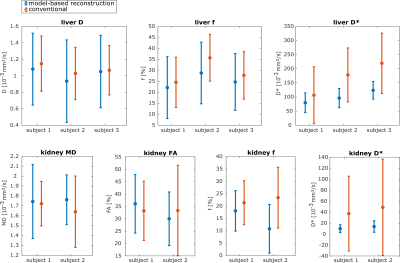
A quantitative comparison of the mean ROI parameter values obtained with model-based and conventional fitting is shown in Figure 5. The mean values and standard deviations were similar. With model-based reconstruction, D was slightly lower in the liver, which could have resulted from cardiac motion artificially increasing D in the conventional fit. In the kidney, MD was slightly higher for model-based fitting, which is consistent with proper handling of Gaussian noise. The model-based reconstruction yielded lower f values in both organs and all datasets. An interesting observation was that the mean and standard-deviation of D* were much lower with model-based reconstruction.

Discussion

Model-based reconstruction for IVIM and IVIM-DTI fitting resulted in good-quality parameter maps. These initial results could help to overcome the challenges in conventional IVIM and IVIM-DTI. We plan to scan more subjects to further optimize regularization parameters and investigate the robustness of the reconstructions. Additionally, we plan to include image acquisition acceleration by undersampling k- and diffusion-space.

Conclusion

We showed the feasibility of IVIM and combined IVIM-DTI model-based reconstructions in liver and kidney.

Acknowledgements

No acknowledgement found.