3417
Lamellar liquid crystal phantom for validating MRI methods to distinguish oblate and prolate diffusion tensors on whole-body scanners
Hong Jiang1, João Pedro de Almeida Martins1, Dan Lundberg2, Chantal M. W. Tax3, and Daniel Topgaard1
1Physical Chemistry, Lund University, Lund, Sweden, 2CR Competence AB, Lund, Sweden, 3Cardiff University Brain Research Imaging Centre (CUBRIC), Cardiff University, Cardiff, United Kingdom
1Physical Chemistry, Lund University, Lund, Sweden, 2CR Competence AB, Lund, Sweden, 3Cardiff University Brain Research Imaging Centre (CUBRIC), Cardiff University, Cardiff, United Kingdom
Synopsis
Conventional diffusion MRI can yield planar tensors in tissues such as epidermoid cysts, comprising tightly packed planar cells, and brain tissue "sheet" structures with populations of axonal fibers crossing at nearly right angles. The two cases may be resolved by multidimensional diffusion encoding as previously demonstrated with various liquid crystal phantoms on preclinical equipment. For method validation also on whole-body scanners, we here develop a lamellar liquid crystal phantom giving microscopically planar diffusion tensors and having sufficiently long T2 for use with single-shot EPI signal read-out.
Introduction
The popularity of DTI1 derives from its ability to convey information about the geometry of microscopic compartments, such as axonal fibers, from their imprint on the water diffusion propagators and tensors.2,3 Ambiguities may arise in cases where the microscopic compartments have some unusual configuration of orientations. As an example, planar diffusion tensors would normally be interpreted as stacks of planar cells, for instance in epidermoid cysts,4 but may also arise from cylindrical structures with multiple orientations in a single plane – a prominent example being the “sheet” structure of fiber bundles crossing at nearly right angles.5-7Diffusion MRI methods with signal acquisition as a function of not only the conventional b-value and vector, but also the “shape”8-11 of the b-matrix,12,13 have potential for disambiguating oblate and prolate compartments even when orientational disorder disrupts the simple relations between the shapes of the microscopic tensors and the voxel-averaged ones observed in conventional DTI.14
For microimaging hardware, these new MRI methods have been validated using liquid crystals with microgeometry tunable by the chemical composition.8,15,16 Liquid crystals with the relevant slab or cylinder compartments typically have too low water content and short T2 for detection at the >50 ms echo times used for single-shot EPI on whole-body equipment. Using methods from the field of surface- and colloid science,17,18 we have developed a reverse hexagonal liquid crystal yielding essentially one-dimensional diffusion on the microscopic level and having >40 wt% water, which is sufficient for use on clinical scanners.19 Expanding on these results, we here develop a lamellar liquid crystal with >85 wt% water and two-dimensional diffusion.
Methods
Liquid crystals were made from water, 1-decanol, and sodium octanoate20,21 at a range of chemical compositions as shown in Figure 1. The phase structure was determined by polarized light microscopy,22 2H NMR spectroscopy,23 and small-angle X-ray scattering (SAXS).24 A lamellar phase (“Lam”) with composition 85.79 wt% water, 9.17 wt% 1-decanol and 5.04 wt% sodium octanoate was selected for further investigations with MRI. Samples in 5 mm NMR tubes and a 0.5 L round flask were prepared for microimaging and the whole-body scanner, respectively. For reference, a micellar solution (“Mic”) and a reverse hexagonal liquid crystal (“Hex”) was prepared as described previously.19Microimaging was performed on a Bruker 500 MHz spectrometer with a 11.7 T magnet and a MIC-5 probe generating 3 T/m gradients. Images were acquired with a spin-echo sequence and RARE image readout25 at 0.3×0.3 mm2 in-plane resolution, 0.6 mm slice thickness, 16×16×1 matrix size, and 50.3 ms echo time, using diffusion encoding with analytically calculated gradient waveforms15 giving 6 b-values up to 11.1·109 sm–2, bΔ = [–0.5, 0, 0.5, 1], and 17 orientations. The 0.5 L sample was studied on a 3 T Connectome system (Siemens Healthcare) with 0.3 T/m gradients. Images were acquired with a spin echo-prepared EPI sequence26,27 at 2×2 mm2 in-plane resolution, 4 mm slice thickness, 96×96×24 matrix size, and 83 ms echo time, using numerically optimized gradients28 giving 6 b-values up to 6·109 sm–2, bΔ = [–0.5, 0, 0.5, 1], and 15 orientations.
For every voxel, Monte Carlo inversion29,30 was employed to convert the acquired signal to nonparametric D-distributions in a primary analysis space of the axial and radial eigenvalues, DA and DR, and the polar and azimuthal angles, θ and φ, which were converted to the isotropic diffusivity Diso = (DA + 2DR)/3, squared normalized anisotropy DΔ2 = (DA – DR)2/(DA + 2DR)2,31 and lab-frame diagonal elements Dxx, Dyy, and Dzz. Parameter maps were generated by calculating means E[x], variances Var[x], and covariances Cov[x,y] over the entirety or sub-divisions (“bins”) of the distribution space.32
Results & Discussion
Figure 1 shows a ternary phase diagram of water, 1-decanol, and sodium octanoate system as well as 2H NMR and SAXS data for a sample with the composition selected for MRI measurements. This sample exhibits a lamellar microstructure with lattice spacing a = 15 nm which is retained up to 29 °C.The quantitative parameter maps in Figure 2 show that all 5 mm samples for microimaging have the expected microstructure: Hex DA/DR > 4 (prolate) and DΔ2 ≈ 1, Mic DA/DR ≈ 1 (spherical) and DΔ2 ≈ 0, and Lam DA/DR < 1/4 (oblate) and DΔ2 ≈ 0.25. The direction-coded maps illustrate the lack of orientational order for in particular the Hex sample. The 0.5 L Lam sample investigated on the whole-body scanner features mainly oblate tensors similar to the 5 mm Lam, but also a central region with prolates indicating that the homogeneity of the sample could be improved, for instance by annealing of the liquid crystal structure via temperature cycling.19
Conclusions
The lamellar liquid crystal gives ample signal in single-shot EPI and features exclusively oblate components in the diffusion tensor distributions obtained on microimaging hardware. Also the 0.5 L phantom for whole-body equipment gives mainly oblates, however having a core with prolates that indicate room for improvement - for instance by annealing to give a perfectly homogeneous lamellar structure suitable for validation of novel diffusion MRI methods on clinical scanners.Acknowledgements
This work was financially supported the Swedish Foundation for Strategic Research (ITM17-0267), Swedish Research Council (2018-03697), and Chinese Scholarship Council. DT owns shares in Random Walk Imaging AB (Lund, Sweden, http://www.rwi.se/), holding patents related to the described methods.References
1. Basser PJ, Mattiello J, Le Bihan D. MR diffusion tensor spectroscopy and imaging. Biophys J 1994;66:259-267. doi: 10.1016/S0006-3495(94)80775-1
2. Price WS. NMR studies of translational motion. Cambridge: Cambridge University Press; 2009.
3. Callaghan PT. Translational dynamics & magnetic resonance. Oxford: Oxford University Press; 2011.
4. Jolapara M, Kesavadas C, Radhakrishnan VV, Saini J, Patro SN, Gupta AK, Kapilamoorthy TR, Bodhey N. Diffusion tensor mode in imaging of intracranial epidermoid cysts: one step ahead of fractional anisotropy. Neuroradiology 2009;51:123-129. doi: 10.1007/s00234-008-0464-9
5. Wedeen VJ, Rosene DL, Wang R, Dai G, Mortazavi F, Hagmann P, Kaas JH, Tseng W-YI. The geometric structure of the brain fiber pathways. Science 2012;335:1628-1634. doi: 10.1126/science.1215280
6. Tax CMW, Dela Haije T, Fuster A, Westin CF, Viergever MA, Florack L, Leemans A. Sheet Probability Index (SPI): Characterizing the geometrical organization of the white matter with diffusion MRI. Neuroimage 2016;142:260-279. doi: 10.1016/j.neuroimage.2016.07.042
7. Tax CMW, Westin CF, Dela Haije T, Fuster A, Viergever MA, Calabrese E, Florack L, Leemans A. Quantifying the brain's sheet structure with normalized convolution. Med Image Anal 2017;39:162-177. doi: 10.1016/j.media.2017.03.007
8. Eriksson S, Lasič S, Nilsson M, Westin C-F, Topgaard D. NMR diffusion encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. J Chem Phys 2015;142:104201. doi: 10.1063/1.4913502
9. Westin C-F, Knutsson H, Pasternak O, Szczepankiewicz F, Özarslan E, van Westen D, Mattisson C, Bogren M, O'Donnell L, Kubicki M, Topgaard D, Nilsson M. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage 2016;135:345-362. doi: 10.1016/j.neuroimage.2016.02.039
10.Topgaard D. Multidimensional diffusion MRI. J Magn Reson2017;275:98-113. doi: 10.1016/j.jmr.2016.12.007
11. Reymbaut A. Diffusion anisotropy and tensor-valued encoding. In: Topgaard D, (Ed.). Advanced Diffusion Encoding Methods in MRI, New Developments in NMR. Cambridge, UK: Royal Society of Chemistry; 2020. p 68 - 102. doi: 10.1039/9781788019910-00068
12. Basser PJ, Mattiello J, Le Bihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B 1994;103:247-254. doi: 10.1006/jmrb.1994.1037
13. Mattiello J, Basser PJ, LeBihan D. Analytical expressions for the b matrix in NMR diffusion imaging and spectroscopy. J Magn Reson A 1994;108:131-141. doi: 10.1006/jmra.1994.1103
14. Topgaard D. NMR methods for studying microscopic diffusion anisotropy. In: Valiullin R, (Ed.). Diffusion NMR of Confined Systems: Fluid Transport in Porous Solids and Heterogeneous Materials, New Developments in NMR. Cambridge, UK: Royal Society of Chemistry; 2016. p 226-259. doi: 10.1039/9781782623779-00226
15. Topgaard D. Director orientations in lyotropic liquid crystals: Diffusion MRI mapping of the Saupe order tensor. Phys Chem Chem Phys 2016;18:8545-8553. doi: 10.1039/c5cp07251d
16. McHugh DJ, Hubbard Cristinacce PL. Phantoms for validating advanced diffusion sequences. In: Topgaard D, (Ed.). Advanced Diffusion Encoding Methods in MRI, New Developments in NMR. Cambridge, UK: Royal Society of Chemistry; 2020. p 349-376. doi: 10.1039/9781788019910-00349
17. Jönsson B, Lindman B, Holmberg K, Kronberg B. Surfactants and polymers in aqueous solution. Chichester: John Wiley & Sons Ltd; 1998.
18. Evans DF, Wennerström H. The colloidal domain: Where physics, chemistry, biology, and technology meet. New York: Wiley-VCH; 1999.
19. Nilsson M, Larsson J, Lundberg D, Szczepankiewicz F, Witzel T, Westin C-F, Bryskhe K, Topgaard D. Liquid crystal phantom for validation of microscopic diffusion anisotropy measurements on clinical MRI systems. Magn Reson Med 2018;79:1817-1828. doi: 10.1002/mrm.26814
20. Ekwall P, Mandell L, Fontell K. Ternary systems of potassium soap, alcohol, and water. J Colloid Interface Sci 1969;31:508-529. doi: 10.1016/0021-9797(69)90052-6
21. Persson N-O, Fontell K, Lindman B, Tiddy GJT. Mesophase structure studies by deuteron magnetic resonance observations for the sodium octanoate-decanoI-water system. J Colloid Interface Sci 1975;53:461-466. doi: 10.1016/0021-9797(75)90063-6
22. Laughlin RG. The Aqueous Phase Behavior of Surfactants. London: Academic Press; 1994.
23. Ferreira TM, Bernin D, Topgaard D. NMR studies of nonionic surfactants. Annu Rep NMR Spectrosc 2013;79:73-127. doi: 10.1016/B978-0-12-408098-0.00003-3
24. Schnablegger H, Yashveer S. The SAXS Guide, Getting acquainted with the principles: Anton Paar GmbH, Austria; 2013.
25. Henning J, Nauerth A, Friedurg H. RARE imaging: a fast imaging method for clinical MR. Magn Reson Med 1986;3:823-833. doi: 10.1002/mrm.1910030602
26. Mansfield P. Multi-planar image formation using NMR spin echoes. J Phys C 1977;10:L55-L58. doi: 10.1088/0022-3719/10/3/004
27. Mansfield P, Pykett IL. Biological and medical imaging by NMR. J Magn Reson 1978;29:355-373. doi: 10.1016/0022-2364(78)90159
28. Sjölund J, Szczepankiewicz F, Nilsson M, Topgaard D, Westin C-F, Knutsson H. Constrained optimization of gradient waveforms for generalized diffusion encoding. J Magn Reson 2015;261:157-168. doi: 10.1016/j.jmr.2015.10.012
29. Prange M, Song YQ. Quantifying uncertainty in NMR T2 spectra using Monte Carlo inversion. J Magn Reson 2009;196:54-60. doi: 10.1016/j.jmr.2008.10.008
30. De Almeida Martins JP, Topgaard D. Multidimensional correlation of nuclear relaxation rates and diffusion tensors for model-free investigations of heterogeneous anisotropic porous materials. Sci Rep. 2018;8(1):1-12.
31. Conturo TE, McKinstry RC, Akbudak E, Robinson BH. Encoding of anisotropic diffusion with tetrahedral gradients: A General mathematical diffusion formalism and experimental results. Magn Reson Med 1996;35:399-412. doi:10.1002/mrm.1910350319
32. Topgaard D. Diffusion tensor distribution imaging. NMR Biomed 2019;32:e4066. doi: 10.1002/nbm.4066
Figures
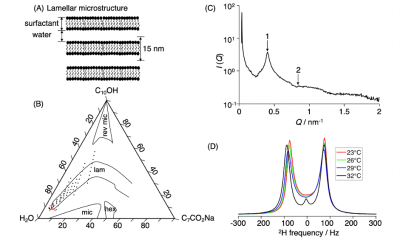
Figure 1. Characterization of the lamellar liquid crystal. (A) Schematic microstructure with a stack of surfactant bilayers intercalated by water. (B) Ternary phase diagram of the sodium octanoate (C7CO2Na) – 1-decanol (C10OH) – water (H2O) system at 23 ºC. The red cross points out the selected composition. (C) SAXS intensity I as a function of scattering vector Q with Bragg peaks (numbered arrows) indicating lamellar stucture with 15 nm lattice spacing. (D) 2H NMR spectra for a series of temperatures showing transition from lamellar (doublet) to micellar solution (singlet) at 32 ºC.

Figure 2. Parameter maps derived from the per-voxel D-distributions for the 5 mm Hex, Mic, and Lam phantoms for microimaging and the 0.5 L Lam phantom on the whole-body scanner. (A) Image segmentation by binning in the 2D Diso-DA/DR projection to capture tensor components characteristic of Hex (prolate), Mic (spherical), and Lam (oblate). (B) Per-voxel statistical measures E[x], Var[x] and Cov[x,y] of the Diso and DΔ2 projections of the distributions. (C) Bin-resolved signal fractions (brightness) and per-bin means (color). Ideal lamellar gives rise to foblate = 1 and DΔ2 = 0.25.