3407
A novel in silico phantom for microstructure, tractography and quantitative connectivity estimation1University Hospital Center (CHUV) and University of Lausanne (UNIL), Lausanne, Switzerland, 2CIBM Center for BioMedical Imaging, Lausanne, Switzerland, 3Swiss Federal Institute of Technology Lausanne (EPFL), Lausanne, Switzerland, 4Univ Rennes, Inria, CNRS, Inserm, IRISA UMR 6074, Empenn ERL U-1228, Rennes, France, 5Technical University of Denmark, Kongens Lyngby, Denmark
Synopsis
In this work, we propose a novel phantom obtained from Monte-Carlo simulations of spins dynamics to improve testing and validation of DW-MRI quantitative structural connectivity. The DiSCo (Diffusion-Simulated Connectivity) phantom is composed of 16 regions of interest placed on a sphere of 1 millimeter in diameter, interconnected by 12,196 axon-like tubular fibers ranging from 1.4um to 4.2um in diameter. Its associated connectivity matrix is weighted by their cross-sectional areas. This in silico phantom, with both microscopic and macroscopic complexity, aims at improving the development and the validation of white matter connectivity estimation methods.
Introduction
The methodological development in the mapping of the brain structural connectome from diffusion-weighted magnetic resonance imaging (DW-MRI) has raised many hopes in the neuroscientific community. In the search for accuracy of the structural connectome, researchers have given particular attention to linking the tractography methods used for generating the connectome with information about the microstructure of the nervous tissue. This “quantitative connectome” has shown promising results 1,2, but the lack of realistic numerical phantoms hindered the development and validation of methods in this framework.Methods
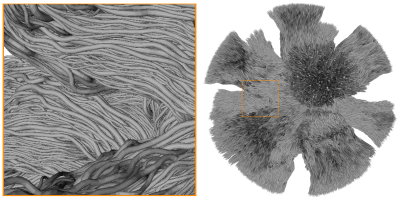
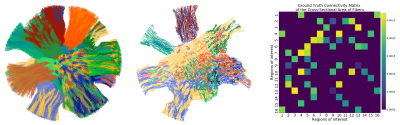
In this work, we have designed a novel dataset of simulated DW-MRI images from a numerical phantom to foster the development of tractography and connectivity methods. The phantom is composed of 12,196 tubular fibers, with gamma-distributed outer diameters ranging from 2um to 6um, connecting distant Regions of Interest (ROIs). The simulation substrates have a micrometric resolution and an unprecedented size of 1 cubic millimeter to mimic an image acquisition matrix of 40x40x40 voxels. Within each voxel, the DW-MRI signal is obtained using Monte-Carlo simulations of spins dynamics using a sampling density of one sample per micrometer cube. The resulting image is then upscaled by a factor 100, for a final image size of 10x10x10cm3 and a voxel size of 2.5mm isotropic, compatible with conventional diffusion tractography methods. The simulated images capture the microscopic properties of the tissue (e.g. fiber diameter, water diffusing within and around fibers, free water compartment), while also having desirable macroscopic properties resembling the anatomy, such as the smoothness of the fiber trajectories. The simulated phantom has 16 ROIs, forming 120 possible connections to distinct pairs of ROIs, among which 25 have tubular fibers connecting them. The values of the 16x16 connectivity matrix correspond to the cross-sectional area of the fiber between pairs of ROIs.The geometrical design of the simulation phantom was done through an iterative optimization process starting from an overlapping set of large tubular fibers (30um in diameter), with both endpoints located in ROIs on the surface of a sphere of 1mm in radius. Each fiber was set to follow the trajectory of an arc of a circle going through the center of the sphere. Those fibers were slowly separated using Numerical Fiber Generator 3, by minimizing energy terms controlling for length, curvature, and overlap with other fibers. Then, they were subdivided into multiple fibers with a smaller diameter (15um), and their trajectories re-optimized. Finally, a set of gamma-distributed diameters were sampled and placed within each fiber to form the final set of axon-like structures. Those were optimized for an additional iteration to ensure the absence of overlapping and the volume preservation of the fibers throughout the substrate. The final set of fibers (trajectories and diameters) were used to generate tubular meshes representing the outer surface of the axon-like structure. Inner tubular meshes following the same trajectory were added with a diameter of 0.7 times the outer diameter, to mimic the presence of myelin sheaths (inner fiber diameter ranging from 1.4um to 4.2um). The meshes were used as input to the Monte-Carlo simulator 4. All samples initiated inside the inner-mesh were considered as “intra-axonal” water, those within the outer-mesh but outside the inner mesh were considered “myelin” water, and those outside the outer-mesh were considered “extra-axonal”. The simulation parameters for the “intra-axonal” and “extra-axonal” water were identical. Only samples initiated inside the “intra-axonal” and “extra-axonal” compartments were used to generate the final signal.
The diffusion protocol includes 360 diffusion-weighted images and four non-diffusion-weighted images (b=0). The diffusion-weighted measurements are distributed on four b-shells (b=1000, 1925, 3094, 13191 s/mm2). Those correspond to the three b-shells of the ActiveAx protocol 5 with an additional shell at b=1000s/mm2 (echo time of 0.0535s). Each shell is sampled using 90 uniformly distributed gradient directions on the sphere.
Results
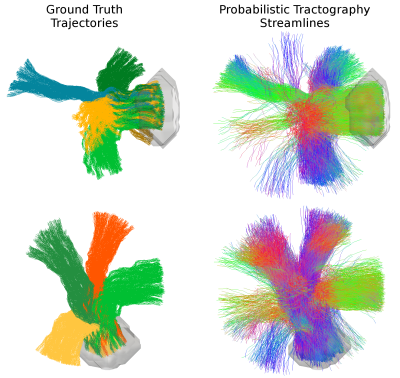
Figure 1 shows the mesh of the substrate used to generate the Diffusion-Simulated Connectivity (DiSCo) dataset. Figure 2 shows the trajectories of the tubular fibers. Figure 3 shows the fraction of Monte-Carlo samples initiated inside the inner tubular mesh and the reconstructed diffusion tensors and fiber orientation distribution functions. Figure 4 shows the tubular fiber trajectories of connections of two ROIs, and the corresponding streamlines reconstructed using tractography 6.Discussion and Conclusions
This dataset was built on previous efforts to test and validate tractography using simulated data 3,7,8. The DiSCo dataset is designed to reproduce the complexity of the nervous tissue at both the microscopic and macroscopic scales, which is fundamental for the accurate representation of the link between the DW-MRI signal and the structural connectivity. This was possible thanks to the engineering of a large-scale Monte Carlo simulation of the particle dynamics which enabled the creation of this phantom of unprecedented size. DiSCo includes an accurate simulation of the microstructure which provides a quantitative aspect of the connectivity. While previous phantoms were dedicated to either validate tractography or microstructure, this dataset provides a tool to better assess the reliability of the connectome estimation on the one hand and of its adherence to the actual microstructure of the nervous tissue on the other hand.Acknowledgements
We acknowledge access to the facilities and expertise of the CIBM Center for Biomedical Imaging, a Swiss research center of excellence founded and supported by Lausanne University Hospital (CHUV), University of Lausanne (UNIL), Ecole polytechnique fédérale de Lausanne (EPFL), University of Geneva (UNIGE) and Geneva University Hospitals (HUG). Marco Pizzolato acknowledges the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 75446. This research project is part of the MMINCARAV Inria associate team program between Empenn (Inria Rennes Bretagne Atlantique) and LTS5 (Ecole polytechnique fédérale de Lausanne — EPFL) started in 2019. Raphaël Truffet’s PhD is partly funded by ENS Rennes.References
1. Daducci, A., Dal Palu, A., Lemkaddem, A., & Thiran, J.-P. (2014). COMMIT: Convex Optimization Modeling for Micro-structure Informed Tractography. IEEE Transactions on Medical Imaging, 34(1).
2. Smith, R. E., Tournier, J. D., Calamante, F., & Connelly, A. (2015). SIFT2: Enabling dense quantitative assessment of brain white matter connectivity using streamlines tractography. NeuroImage, 119, 338–351.
3. Close, T. G., Tournier, J.-D., Calamante, F., Johnston, L. A, Mareels, I., & Connelly, A. (2009). A software tool to generate simulated white matter structures for the assessment of fibre-tracking algorithms. NeuroImage, 47(4), 1288–1300. https://doi.org/10.1016/j.neuroimage.2009.03.077 parameter choice on the reproducibility of results. Frontiers in Neuroinformatics, 14, 8.
4. Rafael-Patino, J., Romascano, D., Ramirez-Manzanares, A., Canales-Rodríguez, E. J., Girard, G., & Thiran, J. P. (2020). Robust Monte-Carlo Simulations in Diffusion-MRI: Effect of the substrate complexity and parameter choice on the reproducibility of results. Frontiers in Neuroinformatics, 14, 8.
5. Alexander, D. C., Hubbard, P. L., Hall, M. G., Moore, E. a., Ptito, M., Parker, G. J. M., & Dyrby, T. B. (2010). Orientationally invariant indices of axon diameter and density from diffusion MRI. NeuroImage, 52(4), 1374–1389.
6. Garyfallidis, E., Brett, M., Amirbekian, B., Rokem, A., Van Der Walt, S., Descoteaux, M., … Dipy Contributors (2014). Dipy, a library for the analysis of diffusion MRI data. Frontiers in Neuroinformatics, 8, 1–5.
7. Maier-Hein, K. H., Neher, P. F., Houde, J. C., Côté, M. A., Garyfallidis, E., Zhong, J., ... & Reddick, W. E. (2017). The challenge of mapping the human connectome based on diffusion tractography. Nature communications, 8(1), 1- 13. Schilling, K. G., Nath, V., Hansen, C., Parvathaneni, P., Blaber, J., Gao, Y., ... & Schiavi, S. (2019). Limits to anatomical accuracy of diffusion tractography using modern approaches. NeuroImage, 185, 1-11.
8. Neher, P. F., Laun, F. B., Stieltjes, B., & Maier-Hein, K. H. (2013). Fiberfox: Facilitating the creation of realistic white matter software phantoms. Magnetic Resonance in Medicine.
Figures