Introduction

Recently, several deep neural networks have been presented for diffusion parameter mapping^1-3. However, these networks allow us to input fixed b-values and fixed diffusion gradient schemes (i.e., gradient direction and the number of gradients) that were used for training. Hence, if data with different b-values or gradient schemes exist, the networks need to be retrained with a new training dataset, requiring long preparation time and efforts. This issue of generalization for the input data is critical for neural networks. In this work, we present a new deep neural network, which is referred to as DIFFnet, that allows us to reconstruct diffusion model parameters from various b-values and gradient schemes. Two DIFFnets were designed: DIFFnet_DTI for diffusion tensor imaging (DTI)^4,5 and DIFFnet_NODDI for neurite orientation dispersion and density imaging (NODDI)⁶. In each model, two in-vivo datasets, which have different b-values and gradient schemes, are evaluated for performance.

Method

[DIFFnet outline] For DTI (Fig. 1a), DIFFnet_DTI was constructed to generate DTI parameters from a diffusion signal set with $$$n_0$$$ number of diffusion gradient directions with a single b-value of $$$b_0$$$ s/mm². For NODDI (Fig. 1b), DIFFnet_NODDI was designed to generate NODDI model parameters from a three-shell protocol, such as $$$n_1$$$, $$$n_2$$$, and $$$n_3$$$ diffusion-weighted signals for b-value of $$$b_1$$$, $$$b_2$$$, and $$$b_3$$$ respectively. DIFFnet was aimed to generate the parameter maps from various b-values, diffusion gradient direction, and the number of gradients.To achieve this goal, a Qmatrix was introduced and utilized for an input of DIFFnet: First, the normalized signals were placed in a q-space with a q-vector as spatial coordinates (Fig. 2b). For DTI, signals were projected on a xy-, yz-, and xz-plane (Fig. 2c), quantized along the two axes by $$$q_n$$$ and concatenated, producing $$$q_n × q_n × 3$$$ matrix. Five different $$$q_n$$$ values, 5, 10, 15, 20, and 25, were tested. For NODDI (Fig. 2c), the projection was performed on each shell, quantized by $$$q_n$$$, and concatenated, producing $$$q_n × q_n × 9$$$ matrix. As a structure of DIFFnet, ResNet was utilized⁷.

[Training dataset generation] Monte-Carlo diffusion simulation was performed to generate the training dataset. For DIFFnet_DTI, to obtain signal set with various gradient schemes, $$$n_0$$$ and $$$b_0$$$ were randomly selected in the range of 30 to 80 and 600 to 1200 s/mm², respectively. For DIFFnet_NODDI $$$n_1$$$, $$$n_2$$$, and $$$n_3$$$ were chosen in the ranges of 5 to 10, 25 to 50, and 50 to 100, respectively. Those for $$$b_1$$$, $$$b_2$$$, and $$$b_3$$$ were sampled in the ranges of 250 to 350, 600 to 800, and 1800 to 2200 s/mm², respectively. A total of 10⁶ protons, assumed to have an unit magnetization each, were generated and performed random walks, following DTI or NODDI diffusion model. The phase of magnetization for each spin was accumulated. After the simulation was performed, a complex-averaged signal was calculated based on the pulsed gradient spin echo sequence. A total of 10⁶ times of simulations were conducted for training in both DTI and NODDI.

[Dataset acquisition & processing] A total of four datasets, with five in-vivo scans each, were used for evaluation. For DTI, Dataset_DTI-A of b = 700 s/mm² with 32 directions and Dataset_DTI-B of b = 1000 s/mm² with 30 directions were utilized. For reference, conventioanl DTI maps were reconstructed⁴. For NODDI, Dataset_NODDI-A of b = 300, 700, and 2000 s/mm² with 8, 32, and 64 directions, and Dataset_NODDI-B of b = 300, 700, and 2000 s/mm² with 8, 30, and 60 directions were used. For reference, conventional NODDI maps were reconstructed⁶.

[Evaluation] In DTI, DIFFnet_DTI was evaluated with Dataset_DTI-A and Dataset_DTI-B. For the comparison, a multi-layer perceptron (MLP)² trained by a simulated dataset having a gradient scheme of Dataset_DTI-A was compared. Similarly, DIFFnet_NODDI and MLP, trained by a dataset having a gradient scheme of Dataset_NODDI-A, was tested with Dataset_NODDI-A and Dataset_NODDI-B. Additionally, accelerated microstructure imaging via convex optimization (AMICO) was tested.

Results

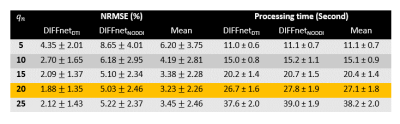
When the effects of five $$$q_n$$$ is investigated (Fig. 3), the results reveal that $$$q_n$$$ of 20 shows the minimum NRMSE, and, therefore, $$$q_n$$$ of 20 is chosen as the default for DIFFnet. In the reconstruction of the DTI maps, DIFFnet_DTI generates highly accurate DTI maps in both datasets (Fig. 4). On the other hand, MLP fails to reconstruct Dataset_DTI-B, which has a different gradient scheme from the training dataset of MLP, demonstrating the importance of the input type generalization in neural networks. Similar trends can be observed in NODDI reconstruction. DIFFnet_NODDI successfully generates the NODDI maps of the two datasets with different gradient schemes (Fig. 5), whereas MLP fails to reconstruct Dataset_NODDI-B. Compared to AMICO results (mean NRMSEs of ICVF:6.24±0.51%, ISOVF:7.21±0.93%, and ODI:8.82±1.25%), DIFFnet_NODDI show lower mean NRMSEs (ICVF:3.78±0.37%, ISOVF:3.61±0.47%, and ODI:7.89±0.44%). Processing time of DIFFnet is measured to be less than 30seconds for all experiments.

Discussion and Conclusion

In this study, DIFFnet was developed to reconstruct the diffusion model parameters from data with various b-value and gradient scheme. Different from previously proposed deep learning methods, which utilized fixed b-values and fixed diffusion gradient schemes, DIFFnet does not specify gradient directions and b-values for its input dataset. In the experiments of DTI and NODDI, DIFFnet demonstrated successful reconstruction for different b-values and gradient scheme datasets.

Acknowledgements

This research was supported by the Brain Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (NRF-2017M3C7A1047864) and NRF grant funded by the Korea government (MSIT) (NRF-2018R1A4A1025891).