3403
A minimal geometrical model for Monte Carlo simulations of time dependent diffusion in axons1Danish Research Centre for Magnetic Resonance, Centre for Functional and Diagnostic Imaging and Research, Copenhagen University Hospital Hvidovre, Hvidovre, Denmark, 2Random Walk Imaging, Lund, Sweden
Synopsis
Understanding the link between axonal geometry and diffusion is of large relevance for diffusion weighted MRI (DW-MRI) of white matter. Identifying the minimal geometrical features needed to describe time dependent diffusion allows for faster simulations adequate for the experimentally feasible level of abstraction. We propose an augmented 1D random walk model that within relevant limits mimics the time dependent diffusion in a 3D model of an axon with varying radius.
Introduction
Linking diffusion to geometry is one central goal of DW-MRI. While analytical descriptions of the signal exist for simple geometries such as planes, cylinders and spheres1–3, many biological tissues have more complex geometries carrying information relevant physiological interpretations of DW-MRI measurements. This has inspired the development of Monte Carlo approaches for simulating the DW-MRI measurement in geometrical models of more complex cell morphologies4. With a particular interest in white matter, the intra-axonal diffusion weighted MR signal has been of particular interest. Increasing the fidelity of geometrical models with the use of histological input is used to render simulations more realistic. However, simplifying substrates down to the major microstructural features affecting the measurements may provide insight into the effect of isolated specific features and may provide more interpretable results5–8. In many experimental settings including those used in clinical settings, the displacements perpendicular to axons are small compared to those probed by the measurements and may be well below the detection limit9. This assumption is also supported by high quality in vivo DW-MRI and DW-MRS data10,11. On the other hand, variations in axonal radius may strongly modulate the mobility along axons on length and time scales relevant for DW-MRI and could be related to the modulated intracellular diffusivity observed in e.g. stroke and multiple sclerosis12,13. These variations could in turn be misinterpreted as variation in e.g. radius or exchange between intra and extracellular domains. In this work we linger on to these effects but only consider the effect of varying fiber diameter which is known from histology14. We demonstrate that the effect on time dependent diffusion from an augmented 1D random walk within realistic limits resembles a 3D simulation. Moreover, the results also highlight that this in turn leads to a scaffold of possible geometries including both the outer boundaries of an axon as well as internal structures such as organelles.Methods
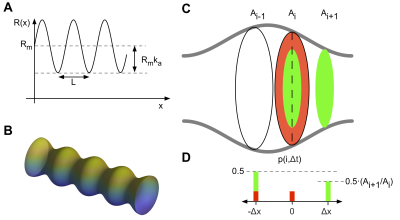
Geometrical substrateAs a test substrate we consider a straight cylinder with a sinusoidally varying radius $$$R$$$ along its axial direction $$$x$$$ (Figure 1 A),
$$
R(x)=R_m+R_m·k_a\cdot\sin(2\pi·x/L)
$$
Where $$$R_m$$$ is the mean radius, $$$K_a$$$ is the relative amplitude and $$$L$$$ is the wavelength. As a gold standard simulation this structure was simulated with the Monte Carlo simulator in the Camino package4. The substrate was constructed as a triangular mesh with circular cross sections (Figure 1 B). One wavelength of the mesh substrate was repeated to infinity through circular boundary conditions.
From 3D to 1D
In our 1D model of the axon we discard the radial position of the walker which corresponds to a full mixing within the cross-sectional plane between each step. The random walk is augmented by adjusting the local step probability. The probability to step from any position into a cross section with a larger area is $$$p$$$=0.5 whereas the step probability into a narrowing section is scaled by the relative cross-sectional area of the destination point as shown in figure 1D. The simulation was implemented in Matlab (Mathworks Inc., USA) using steps on a fixed grid with the step probabilities calculated in advance in a look up table.
Model comparison
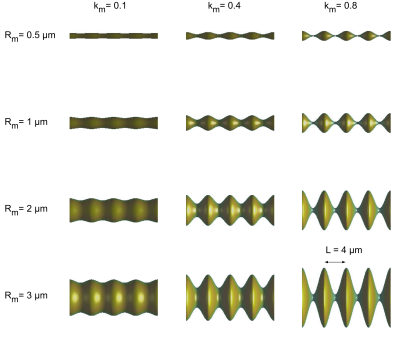
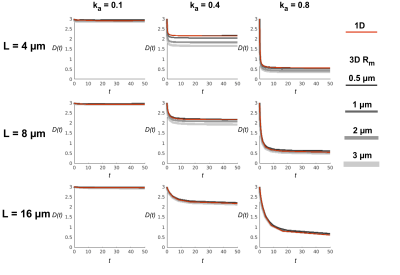
The full 3D and the 1D simulation models were initiated with a uniform initial distribution of 100 000 walkers relative to the cross-sectional area and run with a time step of 0.5 µs, free diffusivity of $$$D_0$$$ = 3.0 µm2/ms. $$$k_a$$$= [0.1, 0.4, 0.8] and $$$L$$$ = [4, 8, 16] µm. The 1D simulation does not depend on absolute radius but the 3D simulation was performed with $$$R_m$$$ set to [0.5, 1, 2, 3] µm. Figure 2 shows examples of all settings of Rmand ka for $$$L$$$ = 4 µm. The random walk trajectories were saved, and diffusion statistics were calculated.
Results
The 1D model was in our implementation 30 times faster than the full 3D model simulated in the Camino software for the same number of walkers and time steps run on a single core CPU. Time dependent diffusivities are shown in figure 3 for the various settings of $$$L$$$ and $$$k_a$$$. The diffusivities estimated from the two simulations are within 5% for cylinders with radius comparable to the mean of human axons ($$$R_a$$$ = 0.5 µm)15 in all settings but diverge for combinations of larger radii, $$$k_a$$$ and short $$$L$$$.Discussion and Conclusion
Fast simulations can account for the dominant morphological features of axons and can be adapted and extended to study other tissue microstructures and additional features such as branching or undulations5,16. This framework can be valuable for the interpretation of data and in exploring novel gradient waveforms designs17. Our simulation suggests that the mean axonal radius has little influence on the mobility along axons but that the wavelength and relative amplitude variation of the cross-sectional area modulate the time dependent behavior to a high degree. We note that $$$k_a$$$= 0.4 predicts a similar tortuosity limit (2/3$$$D_0$$$) in line with observations of intra-axonal water and metabolites18. Our simulation provides equivalent results for typical values of volume weighted axonal radii, varicosities and mitochondrial spacing reported in histology13,15,19,20($$$R_m$$$ ~ 0.5 µm, $$$k_a$$$~ 0.5 and $$$L$$$ approx. 5-20 µm).Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 804746). SL is also supported by Random Walk Imaging.References
1. Stepišnik J. Time-dependent self-diffusion by NMR spin-echo. Phys B. 1993;183:343-350.
2. Callaghan PT. A Simple Matrix Formalism for Spin Echo Analysis of Restricted Diffusion under Generalized Gradient Waveforms. J Magn Reson. 1997;129(1):74-84. doi:10.1006/jmre.1997.1233
3. Barzykin A V. Theory of Spin Echo in Restricted Geometries under a Step-wise Gradient Pulse Sequence. J Magn Reson. 1999;139(2):342-353. doi:10.1006/jmre.1999.1778
4. Hall MG, Alexander DC. Convergence and Parameter Choice for Monte-Carlo Simulations of Diffusion MRI. IEEE Trans Med Imaging. 2009;28(9):1354-1364. doi:10.1109/TMI.2009.2015756
5. Brabec J, Lasič S, Nilsson M. Time-dependent diffusion in undulating structures : Impact on axon diameter estimation. arXiv. 2019:1903.04536.
6. Tanner JE. Transient diffusion in a system partitioned by permeable barriers. Application to NMR measurements with a pulsed field gradient. J Chem Phys. 1978;69(4):1748-1754.
7. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing mesoscopic structural universality with diffusion. Proc Natl Acad Sci. 2014;111(14):5088-5093. doi:10.1073/pnas.1316944111
8. Palombo M, Ligneul C, Najac C, Le J, Flament J, Escartin C. New paradigm to assess brain cell morphology by diffusion-weighted MR spectroscopy in vivo. 2016;113(24):6671-6676. doi:10.1073/pnas.1504327113
9. Nilsson M, Lasič S, Drobnjak I, Topgaard D, Westin C-F. Resolution limit of cylinder diameter estimation by diffusion MRI: The impact of gradient waveform and orientation dispersion. NMR Biomed. 2017;30(7):e3711. doi:10.1002/nbm.3711
10. Veraart J, Fieremans E, Novikov DS. On the scaling behavior of water diffusion in human brain white matter. Neuroimage. 2019;185(June 2018):379-387. doi:10.1016/j.neuroimage.2018.09.075
11. Lundell H, Ingo C, Dyrby TB, Ronen I. Cytosolic diffusivity and microscopic anisotropy of N-acetyl aspartate in human white matter with diffusion-weighted MRS at 7 T. NMR Biomed. 2020. doi:10.1002/nbm.4304
12. Budde MD, Frank JA. Neurite beading is sufficient to decrease the apparent diffusion coefficient after ischemic stroke. PNAS. 2010. doi:10.1073/pnas.1004841107
13. Lee HH, Papaioannou A, Kim SL, Novikov DS, Fieremans E. A time-dependent diffusion MRI signature of axon caliber variations and beading. Commun Biol. 2020. doi:10.1038/s42003-020-1050-x
14. Shepherd GMG, Raastad M, Andersen P. General and variable features of varicosity spacing along unmyelinated axons in the hippocampus and cerebellum. PNAS. 2002;99:6340-6345. doi:10.1073/pnas.052151299
15. Aboitiz F, Scheibel AB, Fisher RS, Zaidel E. Fiber composition of the human corpus callosum. 1992;598:143-153.
16. Palombo M, Ligneul C, Najac C, et al. New paradigm to assess brain cell morphology by diffusion-weighted MR spectroscopy in vivo. Proc Natl Acad Sci U S A. 2016. doi:10.1073/pnas.1504327113
17. Lundell H, Lasič S. Diffusion Encoding with General Gradient Waveforms. In: Advanced Diffusion Encoding Methods in MRI. 1st ed. Royal Society of Chemistry; 2020.
18. Lundell H, Najac C, Bulk M, Kan HE, Webb AG, Ronen. Compartmental diffusion and microstructural properties of human brain gray and white matter studied with double diffusion encoding magnetic resonance spectroscopy of metabolites and water. arXiv. 2020:2012.01796.
19. Abdollahzadeh A, Belevich I, Jokitalo E, Tohka J, Sierra A. Automated 3D Axonal Morphometry of White Matter. Sci Rep. 2019;9(1). doi:10.1038/s41598-019-42648-2
20. Andersson M, Kjer HM, Rafael-Patino J, et al. Axon morphology is modulated by the local environment and impacts the non-invasive investigation of its structure-function relationship. PNAS. 2020;in press.
Figures