3397
Modeling the vascular influences on BOLD fMRI using in vivo brain vasculature: incorporating vessel diameter, orientation, and susceptibility
Michael Bernier1,2, Jeorg Peter Pfannmoeller1,2, Saskia Bollmann3, Avery J.L. Berman1,2, and Jonathan R Polimeni1,2,4
1Department of Radiology, A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Boston, MA, United States, 2Radiology, Harvard Medical School, Boston, MA, United States, 3Centre for Advanced Imaging, University of Queensland, Brisbane, Australia, 4Division of Health Sciences and Technology, Massachusetts Institute of Technology, Boston, MA, United States
1Department of Radiology, A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Boston, MA, United States, 2Radiology, Harvard Medical School, Boston, MA, United States, 3Centre for Advanced Imaging, University of Queensland, Brisbane, Australia, 4Division of Health Sciences and Technology, Massachusetts Institute of Technology, Boston, MA, United States
Synopsis
We have developed a “forward-model” method to calculate the extravascular fields surrounding the blood vessels of the brain that accounts for the vessel diameter and orientation and estimates the field change with activation using in vivo measures of vessel anatomy and blood susceptibility.
Introduction
Although it is well-known that large blood vessels in the brain exert a strong influence on fMRI signals in nearby voxels, which cause artifacts and add noise to the fMRI data, there is a limited number of approaches remove these unwanted effects. Classic approaches sought to identify the large veins in either angiographic data[1] or the fMRI data itself[2] and mask out contaminated voxels, however this strategy does not take into account how the size of the veins and their orientation relative the B0 field, both of which influence the spatial extent of the extravascular field, which is the region surrounding the vessel that will influence the BOLD fMRI signal. Indeed, recent studies have demonstrated that the influence of identified blood vessels on the BOLD fMRI signal falls off with distance from the vessel[3][4], but these studies did not account for how this fall-off would vary as a function of vessel diameter and orientation. Another factor that is not typically considered is the change in the extravascular field with activation, which will, in general, be different from the extravascular field seen around a vein at baseline. To address this, here we have developed a “forward-modeling” method to calculate the extravascular fields surrounding the blood vessels that accounts for the vessel diameter and orientation and estimates the field change with activation. The input to this model is a previously acquired vascular data set consisting of measures of vessel anatomy and blood susceptibility[5]. We present initial results of the predicted extravascular field changes responding to a global activation, and demonstrate how each of these three key features shape the predicted effect.Methods
Ten healthy volunteers (25±5 y.o., 3M/5F) were scanned on a whole-body 7T scanner (MAGNETOM, Siemens Healthineers) using a custom-built head-only receive coil array. To provide an anatomical reference for all vascular data, we acquired T1-weighted MEMPRAGE acquisition (TR/TI/TE1/TE2=2530/1100/1.76/3.7ms, voxel=0.8mm³) as described previously [6]. For QSM, we collected three 3D MEGRE volumes (TR/TE1/TE2=26/9.60/19.20ms, flip=15°, GRAPPA=2×2, voxel=0.5 mm³) at different head angles (neutral, tilted-left, tilted-“chin up”), which were reconstructed with the aspire phase-sensitive coil combination[7]. These data were processed using the Calculation Of Susceptibility through Multi-Orientation Sampling (COSMOS) method paired with a Nonlinear Dipole Inversion (NDI) regularization[8], and indirectly allowed us to reconstruct SWIs[9] at the three angles to ensure a complete venous vessels reconstruction. Cortical surface reconstruction was performed on the MPRAGE data with FreeSurfer, All images were preprocessed previously[10] while the vascular extraction was performed with the updated Braincharter segmentation tool[10], limited to a range between 0.5 and 3.0 mm, which generated a "vesselness" score that was thresholded using random walker to obtain a fine vessel tree. After aligning all images to the T1 anatomical reference using ANTs, the registration was refined using an iterative registration refinement [10] with the ME-ToF and its venous/arterial segmentations in T1 space as a reference in order to improve the multi-modal alignment.The magnetic field $$$\Delta$$$ Boffset from the scanner magnetic field B0 due to the susceptibility of the veins is computed using the finite perturber method In this method the kernel-based convolution for field computation in 3-D space is Fourier transformed to achieve a high computational efficiency. The input mask of the baseline susceptibility X in the veins is used to estimate the susceptibility in the active state using the relation X=X0 Yhemactocrit (1-S02), where X is the susceptibility of fully oxygenated blood, Yhemactocrit is the baseline hematocrit in veins, and (1-S02) is the oxygenation of the blood. Therefore, we determined the in the baseline state and increased the value by 10%[12] .
Results
Figure 1 represents the field offsets projected on flattened and GM surfaces along with the segmented vessels, where the dipole effect surrounding larger vessels is considerate.Discussion and Conclusion
Here we present a framework for estimating field offsets surrounding major blood vessels as a means to infer their influence on nearby BOLD fMRI data that accounts for several factors that influence the extravascular field. This approach may be viewed as a generalization of the classic approach that accounts for large-vein affects based on their image phase, which is a function of the vessel orientation relative to the B0 field[13]. This forward-modeling approach can be easily extended to incorporate more details of the specific BOLD fMRI acquisition, such as echo time and readout duration, and to other forms of fMRI contrast beyond gradient-echo BOLD. Future work will validate the predictions of large-vessel influences using resting-state fMRI data[14] and extend investigations of large-vessel effects on patterns of cortical columns[15].Acknowledgements
This work was supported in part by the NIH NIBIB (grants P41-EB030006 and R01-EB019437), NINDS (grant R21-NS106706), by the BRAIN Initiative (NIH NIMH grant R01-MH111419), and by the MGH/HST Athinoula A. Martinos Center for Biomedical Imaging; and was made possible by the resources provided by NIH Shared Instrumentation Grants S10-RR023043 and S10-RR019371References
[1] P. J. Koopmans and E. Yacoub, “Strategies and prospects for cortical depth dependent T2 and T2* weighted BOLD fMRI studies,” Neuroimage, doi: 10.1016/j.neuroimage.2019.03.024. [2] K. Kay, K. W. Jamison, L. Vizioli, R. Zhang, E. Margalit, and K. Ugurbil, “A critical assessment of data quality and venous effects in sub-millimeter fMRI,” Neuroimage, doi: S1053811919300928. [3] J. Bause et al., “Impact of prospective motion correction, distortion correction methods and large vein bias on the spatial accuracy of cortical laminar fMRI at 9.4 Tesla,” Neuroimage, vol. 208, p. 116434, Mar. 2020, doi: 10.1016/j.neuroimage.2019.116434. [4] M. Moerel et al., “Sensitivity and specificity considerations for fMRI encoding, decoding, and mapping of auditory cortex at ultra-high field,” Neuroimage, vol. 164, pp. 18–31, Jan. 2018, doi: 10.1016/j.neuroimage.2017.03.063. [5] M. Bernier, N. E. Fultz, B. Bilgic, S. Bollmann, and J. R. Polimeni, “Multimodal quantitative arterial-venous segmentation of the human brain at 7T: structure, susceptibility and flow,” in Proc Intl Soc Mag Reson Med., 2020, p. 28:0158. [6] N. Zaretskaya, B. Fischl, M. Reuter, V. Renvall, and J. R. Polimeni, “Advantages of cortical surface reconstruction using submillimeter 7 T MEMPRAGE,” Neuroimage, vol. 165, pp. 11–26, Jan. 2018, doi: 10.1016/j.neuroimage.2017.09.060. [7] K. Eckstein et al., “Computationally Efficient Combination of Multi-channel Phase Data From Multi-echo Acquisitions (ASPIRE),” Magn. Reson. Med., vol. 79, no. 6, pp. 2996–3006, Jun. 2018, doi: 10.1002/mrm.26963. [8] D. Polak et al., “Nonlinear Dipole Inversion (NDI) enables Quantitative Susceptibility Mapping (QSM) without parameter tuning,” Sep. 2019, Accessed: Nov. 02, 2019. [Online]. Available: http://arxiv.org/abs/1909.13692. [9] E. M. Haacke, Y. Xu, Y.-C. N. Cheng, and J. R. Reichenbach, “Susceptibility weighted imaging (SWI),” Magn. Reson. Med., vol. 52, no. 3, pp. 612–618, Sep. 2004, doi: 10.1002/mrm.20198. [10] M. Bernier, S. C. Cunnane, and K. Whittingstall, “The morphology of the human cerebrovascular system,” Hum. Brain Mapp., vol. 39, no. 12, pp. 4962–4975, Dec. 2018, doi: 10.1002/hbm.24337. [11] E. S. Lein et al., “Genome-wide atlas of gene expression in the adult mouse brain,” Nature, vol. 445, no. 7124, pp. 168–176, Jan. 2007, doi: 10.1038/nature05453. [12] K. Uludağ and P. Blinder, “Linking brain vascular physiology to hemodynamic response in ultra-high field MRI,” Neuroimage, vol. 168, pp. 279–295, Mar. 2018, doi: 10.1016/J.NEUROIMAGE.2017.02.063. [13] R. S. Menon, “Postacquisition suppression of large-vessel BOLD signals in high-resolution fMRI.,” Magn. Reson. Med., vol. 47, no. 1, pp. 1–9, Jan. 2002, Accessed: May 24, 2017. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/11754436. [14] J. E. Chen et al., “Resting-state ‘physiological networks,’” Neuroimage, vol. 213, Jun. 2020, doi: 10.1016/j.neuroimage.2020.116707. [15] S. Nasr, J. R. Polimeni, and R. B. H. Tootell, “Interdigitated Color- and Disparity-Selective Columns within Human Visual Cortical Areas V2 and V3,” J. Neurosci., vol. 36, no. 6, pp. 1841–1857, Feb. 2016, doi: 10.1523/JNEUROSCI.3518-15.2016.Figures
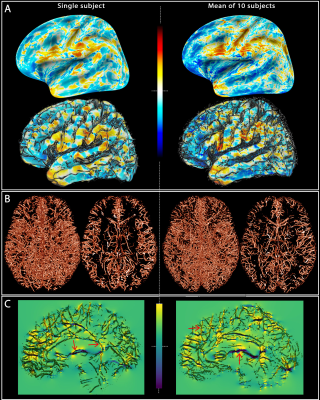
Fig. 1: Field offsets
surrounding major blood vessels The left panels illustrate the results for a single-subject while the right panels are the mean computed for all the subjects. (A) The field offset are projected on both inflated and GM surfaces obtained using Freesurfer. (B) The segmented vessels, illustrated in 3D and in a cross-section (20 mm), are overlapped on the delta B maps (C) to show the strong dipole effects surrounding the vessels perpendicular and parallel to B0 (red arrows).