3342
Investigation of respiration-induced changes of the scattering matrix by EM simulations and a breathing body model1Physikalisch-Technische Bundesanstalt (PTB), Braunschweig and Berlin, Germany, Berlin, Germany, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States
Synopsis
Respiratory motion is a fundamental challenge for thorax MR imaging, particular at ultra-high fields. Recent in-vivo studies have shown that the coil's time-dependent scattering matrix (S-Matrix) can be used for respiration gating to minimize those artefacts. Here, we present electromagnetic simulations of the respiration-induced changes of the transmit RF coil’s S-matrix. Analysing the impact of breathing patterns (conventional, chest, abdominal) illustrates the combined effects of chest/diaphragm motion. The type of respiratory motion and RF coil geometry, position and element type are shown to impact the S-Matrix with implications on coil performance, respiratory triggering, power monitoring and RF pulse design.
INTRODUCTION
Respiratory motion is a well-known problem for thoracic imaging. At UHF ($$$B_0\geq7T$$$) this is even more pronounced as navigators are more difficult to use because of limited $$$B_1^+$$$[1] and self-navigation at UHF is still under investigation [2]. A recent 7T-study investigated the use of an alternative respiration detection method, which determines respiration-induced variations of the scattering matrix (S-Matrix) using a parallel transmission system [3]. Despite successful respiration detection, the measured changes varied between elements of the 8-channel coil and it is still unclear if and how far other factors, such as the coil's position, coil design and respiration pattern have an impact.In this work, we demonstrate that an electromagnetic (EM) simulation with a respiration body model is highly suitable to investigate such respiration-induced S-Matrix changes in detail. We examine the impact of breathing patterns (conventional, chest and abdominal breathing), of coil-body setups, of coil elements (loop vs. dipoles) and location of the individual elements on respiration-induced S-Matrix variations. Finally, such EM simulation-based S-Matrix changes are compared to those found previously in-vivo.
METHODS
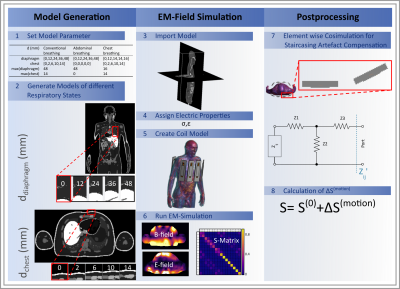
Finite-difference time-domain (FDTD) EM simulations were performed with Sim4Life 6.0 (ZMT) using a 7T 16-TX/RX-channel body array coil (8 modules consisting of 1 dipole + 1 loop element each; cf.Fig.1.5)[4,5]. The coil was loaded by different respiration-resolved body models that were generated for different respiratory states using XCAT[6]. Conductivity and relative permittivity were assigned according to [7] (Fig.1.4).Three breathing patterns varing by diaphragm and chest displacement were modelled: abdominal, chest, and conventional (i.e. chest+abdominal) breathing (Tab. 1). Models in five respiratory states were generated for each breathing pattern. The fifth state refers to maximum inhalation which can exceed displacement by~50% compared to deep breathing, according to own measurements. Two RF coil setups were investigated for deep, conventional breathing: a spatially fixed coil setup [8,9], generating varying minimum distances of 10-30mm between chest and modules and a moving coil setup where the anterior modules move simultaneously with respiration ensuring a 10mm fixed minimum coil-body distance. For abdominal breathing the chest does not move, which motivates using only the fixed coil setup. For chest breathing we chose the moving coil setup which better reflects the experimental situation.
For each of the 20 simulations (5 respiratory states; 4 combinations of breathing pattern and coil setup) a complex S-Matrix was extracted (Fig.1.6). An elementwise co-simulation performed in Python (3.7) compensates staircasing artefacts in rotated elements, introduced by the meshing process (Fig.1.7).
The 16x16 S-Matrix elements are defined by: $$S_{ij}(t)=\frac{V_{fwd,i}}{V_{ret,j}}$$ with $$$V_{fwd,i}$$$forward voltage at channel i, $$$V_{ret,j}$$$: returned voltage at channel j[3]. (Fig.1.8) is decomposed into a time-invariant and a time-varying respiration-induced component[3]: $$S_{ij}(t)=S_{ij}^{(0)}+\Delta S_{ij}^{(motion)}(t)$$
RESULTS
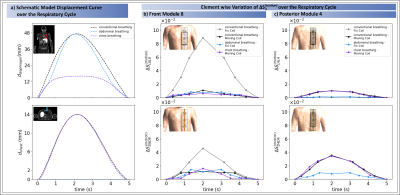
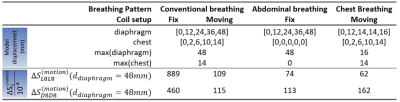
The highest $$$|\Delta S_{ij}^{(motion)}|$$$ changes occur by Loop 8 for the fixed coil setup and conventional breathing of $$$|\Delta S_{L8L8}^{(motion)}|=8.89\cdot10^{-2}$$$ (cf. Fig.2+Tab.1). An order of magnitude smaller values were observed for the other three setups (Tab.1). Depending on the location of the module, different sensitivities to variations in surface and internal geometries were observed. Generally, the central posterior dipoles appear to be more sensitive than the posterior loops ($$$4^{th}$$$ and $$$5^{th}$$$ module, Fig.2). The opposite is observed for the front elements for conventional breathing/fix setup (Figs.2&4). This might be caused by higher spatial coverage of loops and a larger penetration depth of the dipoles. Fig.3 exemplarily shows the SD of $$$\Delta S_{ij}^{(motion)}$$$ over all respiratory states for the moving coil with conventional breathing. Strongest variations are observed on the diagonal matrix elements (i=j, Fig.3),. This is followed by $$$S_{i\neq j}$$$ when j is either the neighbouring module of i or the loop/dipole element of the same TX-module. Similar observations were made for the other patterns/setups.The largest $$$\Delta S^{(motion)}$$$-variation is clearly seen for front modules (Fig.4b) during conventional breathing/fixed coil (gray curve). Posterior elements (Fig.4c) show no relevant difference in $$$\Delta S^{(motion)}$$$ between moving (black curve) and fix setup for conventional breathing. Both findings reflect, as expected, the coil-body distance plays an essential role. For posterior elements the diaphragm motion (blue curve) appears to be less relevant compared to the chest motion (violet curve), this is not observed for front elements. Fig.4b shows similar variations of $$$\Delta S^{(motion)}$$$ for conventional breathing/moving coil, abdominal and chest breathing.
DISCUSSION AND CONCLUSION
This work investigates respiration-induced changes of the S-Matrix by using a dedicated EM simulation with a respiration-resolved body model. Overall, the results confirm experimental results by Hess et al.[3], where variations of up to $$$10^{-3}$$$ were found. Here, however, values up to $$$9 \cdot 10^{-2}$$$ were obtained, which may be related to different coil-element sizes and larger peak diaphragm/chest displacements ($$$d_{diaphragm}$$$=48mm/$$$d_{chest}$$$=14mm) compared to experiments. Fixed coil setups seem preferable over moving setups for motion detection based on S-matrix changes, however, recent work showed higher respiration-induced variations of SAR for this setup[4].In conclusion, the separate investigation of diaphragm and chest motion indicates $$$\Delta S_{ii}^{(motion)}$$$ of posterior elements appears less sensitive for diaphragm motion, but none of the motions dominates the impact on $$$\Delta S_{ii}^{(motion)}$$$ of front elements. In this case both motion types have rather similar relevance for $$$\Delta S_{ii}^{(motion)}$$$ and both affect coil performance, pulse design and power monitoring.
Acknowledgements
This work was supported by the German Research Foundation (DFG), grant number SCHM 2677/2-1.References
[1] S. Schmitter, S. Schnell, K. Uğurbil, M. Markl, and P. F. Van de Moortele, “Towards high-resolution 4D flow MRI in the human aorta using kt-GRAPPA and B1+ shimming at 7T,” J. Magn. Reson. Imaging, vol. 44, no. 2, pp. 486–499, 2016.
[2] S. Dietrich et al., “3D Free‐breathing multichannel absolute Mapping in the human body at 7T,” Magn. Reson. Med., no. October, p. mrm.28602, Dec. 2020.
[3] A. T. Hess, E. M. Tunnicliffe, C. T. Rodgers, and M. D. Robson, “Diaphragm position can be accurately estimated from the scattering of a parallel transmit RF coil at 7 T,” Magn. Reson. Med., vol. 79, no. 4, pp. 2164–2169, Apr. 2018.
[4] N. Schön et al., “Impact of respiration on B1+ field and SAR distribution at 7 T using a novel EM simulation setup,” Proc. Intl. Soc. Mag. Reson. Med., no. 1120, 2020.
[5] M. A. Ertürk, A. J. E. Raaijmakers, G. Adriany, K. Uğurbil, and G. J. Metzger, “A 16-channel combined loop-dipole transceiver array for 7 Tesla body MRI,” Magn. Reson. Med., vol. 77, no. 2, pp. 884–894, 2017. [6] W. P. Segars, G. Sturgeon, S. Mendonca, J. Grimes, and B. M. W. Tsui, “4D XCAT phantom for multimodality imaging research,” Med. Phys., vol. 37, pp. 4902–4915, 2010.
[7] Itis Foundation, “Dielectric Properties.” [Online]. Available: https://itis.swiss/virtual-population/tissue-properties/database/dielectric-properties/%0A.
[8] J. T. Vaughan et al., “Whole-body imaging at 7T: Preliminary results,” Magn. Reson. Med., vol. 61, no. 1, pp. 244–248, 2009.
[9] S. Orzada et al., “A 32-channel parallel transmit system add-on for 7T MRI,” PLoS One, vol. 14, no. 9, pp. 1–20, 2019.
Figures