Introduction

The efficacy of abdominal radiotherapy is reduced by organ motion during treatments, of which respiratory-induced motion forms a large portion. The recently introduced MR-LINAC^[1], a combination of an MR-scanner and radiotherapy LINAC, holds the promise to increase the efficacy of the treatments, if this motion can be tracked in real-time (>5Hz^[2]).

To this extent, we have previously introduced MR-MOTUS^[3,4], which enables real-time non-rigid 3D motion estimation in 160ms. This latency satisfies clinical requirements^[2] and the reconstructions are promising, but the experimental setting requires improvement; data was acquired from one volunteer with the body coil, it required long breath-holds to obtain a reference image, and the validation was problematic due to time-resolution limitations for image-based motion estimation. Most importantly, the framework was demonstrated on a conventional MR-scanner rather than an MR-LINAC, which typically provides lower quality MR-data due to inferior radiolucent receive arrays.

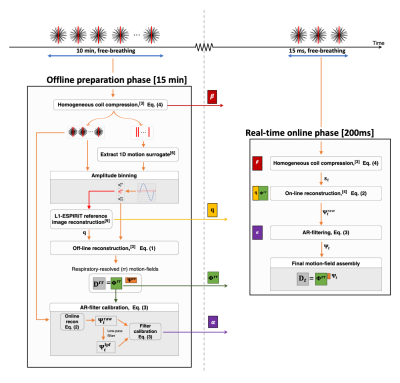
In this work we tighten the gap towards clinical application, and extend MR-MOTUS to a realistic experimental setting on an MR-LINAC, that allows for robust real-time reconstruction of non-rigid 3D motion from multi-coil data acquired in free-breathing. Data acquisition is interleaved with a spoke along feet-head (FH) direction that provides 1D respiratory-motion information for binning and validation^[6]. Motion-fields are reconstructed for 5 volunteers, and validations are performed at 130ms temporal resolution through the newly inserted FH-spokes. Figure 1 shows an overview of the complete framework.

Theory

Real-time MR-MOTUS reconstructions
A low-rank motion-model^[3] is applied to split 3D+t motion-fields $$$\mathbf{D}\in\mathbb{R}^{3N\times {M}}$$$ in a spatial part $$$\boldsymbol{\Phi}\in\mathbb{R}^{3N\times{R}}$$$ and a temporal part $$$\boldsymbol{\Psi}=[\boldsymbol{\Psi}_1^T,\dots,\boldsymbol{\Psi}_M^T]^T\in\mathbb{R}^{M\times{R}}$$$: $$$\mathbf{D}=\boldsymbol{\Phi}\boldsymbol{\Psi}^T$$$. Here $$$N,M,R$$$ denote respectively the number of voxels, dynamics, and rank of the motion model. The low-rank model allows to split 3D+t motion-field reconstructions in a large-scale offline phase to reconstruct a low-rank basis, and a small-scale real-time phase to reconstruct low-dimensional representation coefficients$$$\hspace{.2cm}\boldsymbol{\Psi}^\textrm{raw}_t$$$:$$\mathbf{[Offline]}\hspace{2.5cm}\{\boldsymbol{\Phi}^\textrm{rr},\boldsymbol{\Psi}^\textrm{rr}\}=\textrm{arg}\min_{\boldsymbol{\Phi},\boldsymbol{\Psi}}\hspace{0.5cm}\sum_{t=1}^M \lVert \mathbf{F}(\boldsymbol{\Phi}\boldsymbol{\Psi}_t^T{|}\mathbf{q})-\mathbf{s}_t\rVert_2^2+\lambda_{1}\textrm{TV}(\boldsymbol{\Phi}\boldsymbol{\Psi}_t^T),\hspace{3cm}(1)$$$$\mathbf{[Real\textrm{-}time]}\hspace{2.1cm}\boldsymbol{\Psi}_t^{\textrm{raw}}=\textrm{arg}\min_{\boldsymbol{\Psi}_t}\hspace{0.5cm}\lVert{\mathbf{F}}(\boldsymbol{\Phi}^\textrm{rr}\boldsymbol{\Psi}_t^T{|}\mathbf{q})-\mathbf{s}_t\rVert_2^2+\lambda_{2}\lVert \boldsymbol{\Psi}_{t-1}\rVert_2^2,\quad\textrm{for }t\ge{0},\hspace{2.5cm}(2)$$with $$$\boldsymbol{\Psi}_{0}=\mathbf{0}$$$. In Eq (1-2), $$$\mathbf{F}$$$ is the MR-MOTUS model^[3], $$$\mathbf{q}\in\mathbb{C}^{N}$$$ is a reference image, $$$\mathbf{s}_t\in\mathbb{C}^{N_k}$$$ is the (non-Cartesian) $$$k$$$-space data at dynamic $$$t$$$, TV is the vectorial total-variation^[7], and $$$\lambda_1,\lambda_2>0$$$ denote regularization parameters. Eq. (1) is solved with 60 iterations of L-BFGS^[8] in 15 minutes, and Eq. (2) is solved with a single Gauss-Newton iteration in 160ms.

Real-time filtering
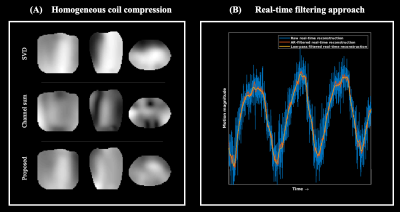
Eq. (2) is solved with 3 spokes of $$$k$$$-space data, resulting in noise-sensitive reconstructions that can be improved with real-time filtering. A typical low-pass FIR-filter induces an undesirable delay of ~1.5 seconds. We propose to calibrate auto-regressive-filter (AR-filter) coefficients $$$\boldsymbol{\alpha}\in\mathbb{R}^{N_f}$$$ to delay-corrected, low-pass-filtered (LPF) reconstructions $$$\boldsymbol{\Psi}^{\textrm{lpf}}$$$ by solving$$\sum_{j=0}^{N_f-1}{{\alpha}_j}\boldsymbol{\Psi}^{\textrm{raw}}_{t-j}=\boldsymbol{\Psi}^{\textrm{lpf}}_t\hspace{3cm}(3)$$for a time-window per volunteer (see Methods) through least-squares. The proposed AR-filtering is delay-free and takes$$$\hspace{.15cm}\approx{10}^{-7}$$$seconds/dynamic.

Homogeneous channel combination in k-space
The model $$$\mathbf{F}$$$ in Eq. (1-2) assumes single-channel k-space data with homogeneous sensitivity (body-coil). To allow multi-coil acquisitions, a linear channel combination with coefficients $$$\boldsymbol{\beta}\in\mathbb{C}^{N_c}$$$ is designed to approximate a homogeneous sensitivity:$$\min_{\boldsymbol{\beta}}\lVert{\mathbf{S}\boldsymbol{\beta}-\mathbf{1}}\rVert_2^2\quad\Leftrightarrow\quad{}\boldsymbol{\beta}=(\mathbf{S}^H\mathbf{S})^{-1}\mathbf{S}^H\mathbf{1},\hspace{3cm}(4)$$where $$$\mathbf{S}\in\mathbb{C}^{N\times{N_c}}$$$ and $$$\mathbf{1}\in\mathbb{C}^{N}$$$ denote respectively the coil sensitivities and an all-one vector.

Methods

Data is acquired with a 1.5T MR-LINAC^[1] (Elekta Unity, Elekta AB, Stockholm, Sweden) from 5 different volunteers (BMI=19.5-27.2,AGE=22-44) during 10 minutes of free-breathing, using an 8-element radiolucent coil, and a 3D golden-mean radial kooshball trajectory^[5] interleaved with a FH spoke every 31 spokes (TR/TE=4.8/1.8ms,FA=20^o,BW=540Hz). All multi-channel data is compressed with $$$\boldsymbol{\beta}$$$ (Eq. (4)). A surrogate signal is extracted from the FH-projections with PCA.^[6] After amplitude-binning, a reference image is reconstructed in mid-ventilation at two spatial resolutions with L1-ESPIRiT using BART^[9]: $$$6.7\times6.7\times6.7{\textrm{mm}^3}$$$ for motion-field reconstructions, $$$3\times3\times3{\textrm{mm}^3}$$$ for visualizations.

First, Eq. (1) is solved with an $$$R=1$$$ motion model, and respiratory-sorted data. Subsequently, Eq. (2) is solved for 50 seconds of data with 3 spokes/dynamic, and 8 samples per spoke to minimize reconstruction times. The first half of this data is used to estimate AR-filter coefficients through Eq. (3) with $$$N_f\in[1;700]$$$, and the second half to independently determine the optimal $$$N_f$$$ through the RMSE. Finally for another 50 seconds of data, solving Eq. (2) is interleaved with AR-filtering, in 160ms/dynamic.

An overview of the complete reconstruction pipeline is shown in Fig. 1.

Results

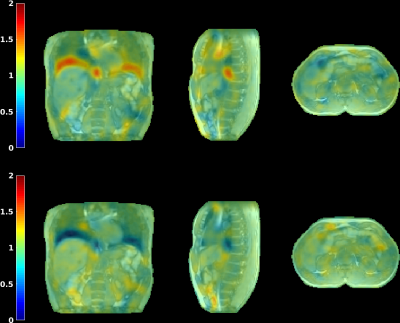
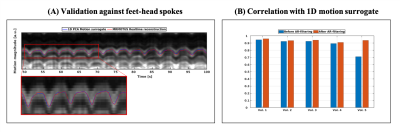
Fig. 2 visualizes the coil compression and real-time filtering, and Fig. 3 the reconstructed motion-fields.

Fig. 4 and 5 show respectively the validation with Jacobian determinants, and the 1D motion information.

It can be observed that realistic motion-fields are reconstructed; determinants are close to unity within most organs, complying with volume-preservation properties^[10], and high Pearson correlation coefficients are obtained with the motion surrogate. Fig. 5 also shows the effectivity of the AR-filter, which increases correlations from 0.88$$$\pm$$$0.097 to 0.94$$$\pm$$$0.018.

For one motion-field dynamic, data acquisition takes 14.4ms, and the reconstruction and filtering takes 160ms on a desktop PC, yielding a total latency of 174.4ms.

Discussion & Conclusion

We extended MR-MOTUS to a robust workflow on an MR-LINAC. Reconstructions were performed on five volunteers and were validated spatially, and at high temporal resolution, showing 0.94$$$\pm$$$0.018 correlation with a 1D motion surrogate. The offline reconstructions (Eq. (1)) take 15 minutes and could be improved with hardware/software accelerations. The total latency of real-time reconstructions (Eq. (2)) is 174.4ms (acquisition+reconstruction) and satisfies clinical requirements for MR-guided radiotherapy (>5Hz^[2]). In conclusion, this work shows the feasibility of real-time 3D motion estimation with MR-MOTUS in a practical setting on an MR-LINAC, thereby tightening the gap to clinical application.

Acknowledgements

This research is funded by the Netherlands Organisation for Scientific Research (NWO), domain Applied and Engineering Sciences, Grant number 15115.