3339

Magnitude Least Squares RF Shimming with Singular Vector Minibatching

Jonathan B Martin¹, Benjamin M Hardy², and William A Grissom¹
¹Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, ²Physics and Astronomy, Vanderbilt University, Nashville, TN, United States

Synopsis

Magnitude-least squares optimization is widely used to design RF shims that produce homogeneous B₁⁺ fields at high field strengths, but the MLS optimization problem is non-convex and prone to becoming stuck in local minima corresponding to unacceptable voids in the shimmed field. We describe a simple, improved Gerchberg-Saxton algorithm for MLS RF shimming in which randomly selected subsets of the B₁⁺ map matrix's singular vectors are used in each shim update. Shims are then refined using conventional GS. Simulations of 8- and 30-channel head coils at 7T verify the method's robustness, and demonstrate advantages over conventional RF shim design techniques.

Introduction

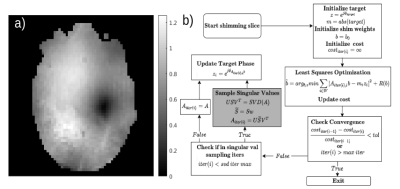
Parallel transmit radiofrequency (RF) shimming is a powerful technique for mitigating $$$B_1^+$$$ inhomogeneity at high field strengths via adjustment of the driving magnitude and phase of elements in a multi-coil transmit array. Framing shim design as a magnitude least squares (MLS) optimization problem provides advantages over linear least squares (LLS) formulations in applications where the magnitude of the transmit profile is primarily of interest^1,2. However, the MLS optimization problem is non-convex, and thus iterative algorithms are prone to falling into local minima rather than returning globally optimal shim solutions. The $$$B_1^+$$$ magnitude profiles corresponding to these local minima often contain voids (Figure 1a), which render shims unusable. In this work, we propose a modified two-stage version of the Gerchberg-Saxton (GS) algorithm commonly used in MLS RF shimming to increase robustness against voids.

Algorithm

Conventional GS reformulates the MLS problem $$arg_{b}min|| |Ab|-m||^{2}_2+R(b)$$ as $$arg_{b,z}min\sum_{i \in W}\{|A_ib-m_iz_i|^{2}+R(b)\}$$ $$s.t. |z_i|=1$$ where $$$i$$$ indexes row. The GS algorithm then alternates between updating target phase $$$z_i$$$ and solving the reformulated LS optimization problem to update $$$b$$$. Our proposed singular vector minibatching GS algorithm is outlined in Figure 1b, an approach inspired by recent work on minibatching in optical phase retrieval^3,4. We begin by performing GS updates in which the $$$N_s \times N_c$$$ parallel transmission system matrix⁵ $$$A$$$ is replaced each iteration by a low-rank approximation created by randomly masking the SVD components $$$USV^T$$$ with uniform probability distribution. For a rank-k approximation of $$$A$$$, we produce a sampling vector $$$w$$$, in which $$$k$$$ random elements are nonzero. $$$w$$$ is then used to mask the submatrices of $$$USV^T$$$, and the new $$$A_{iter(i)}$$$ is reformulated from the reduced set. Once a specified number of iterations with random low-rank $$$A_{iter(i)}$$$ are completed, the algorithm transitions to conventional GS iterations to refine the shims until stopping criteria are met.

Methods

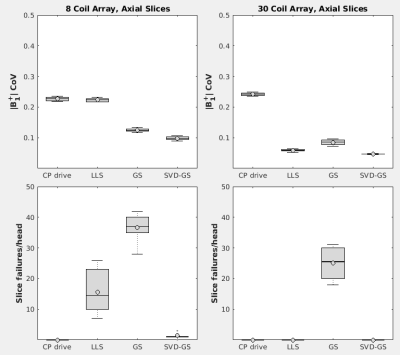
To evaluate the algorithm two 10-subject datasets of $$$B_1^+$$$ maps were generated via simulation of 8-channel and 30-channel loop coils in HFSS (Ansys Inc., Canonsburg, PA, USA) with 20x20x14 cm FOV and 2 mm isotropic voxel size. Each head was shimmed slice-by-slice in the axial plane for the 8-channel coil, and in the axial, sagittal, and coronal planes for the 30-channel coil. The proposed algorithm was implemented as 30 singular vector minibatching iterations, followed by conventional GS iterations until stopping criteria were met. Tikhonov regularization was used, with $$$R(b)=\beta||b||^2_2$$$ and $$$\beta=s\sqrt{\frac{1}{n}\sum_{x,y,z,c}|B_{1,head}^+|^2}$$$, where $$$s$$$ was a scaling factor. $$$\beta$$$ was rounded to 1 significant figure to reduce data type sensitivity.

The algorithm was evaluated in three ways. We compared to conventional GS optimization for four different initial shims: random, CP, spectrally initialized⁶, and unit magnitude with 0 phase, with regularization scaling $$$s=$$$10 and mini-batch size $$$k=$$$3 and 10 for 8 and 30 coils. Second, a parameter space of regularization value ($$$s$$$) versus mini-batch size ($$$k$$$) was constructed for each coil/geometry combination, with random shim initialization. Finally, the performance of four shimming techniques was compared: direct CP drive, LLS shimming, MLS shimming with conventional GS, and our two-stage MLS GS approach with $$$k=$$$3 and 10 for the 8 and 30 channel datasets. $$$s=$$$10 was used for all optimizers. In each experiment, each slice in the dataset of 10 heads was shimmed once. $$$|B_1^+|$$$ coefficient of variation (CoV) and the number of voids were recorded for each slice. A failure slice was defined as a slice with a void present at the end of optimization. Computation was performed on a NVIDIA RTX 2080 GPU with 11 GB memory using SigPy's RF pulse design tools⁷.

Results

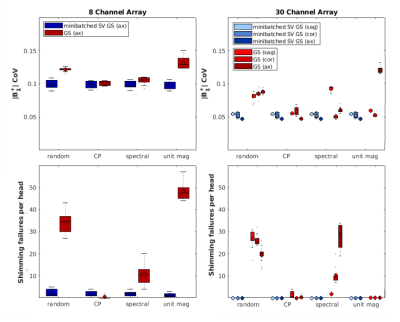
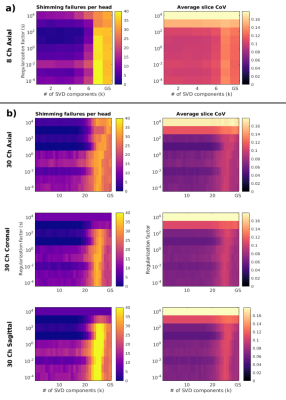
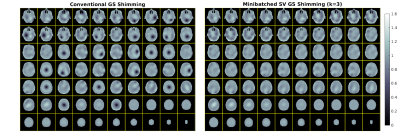
Figure 2 shows boxplots of average slice $$$|B_1^+|$$$ CoV and average number of failure slices per head for the various initializers examined. Figure 3 shows the average number of failure slices per head and average slice $$$|B_1^+|$$$ CoV as a function of regularization and minibatch size $$$k$$$. The far right column of each parameter space plot corresponds to conventional GS, in which $$$k=N_c$$$. For regularization scaling values in the range of $$$10^1$$$ to $$$10^2$$$ and for $$$k$$$ less than 2/3 of full rank, the algorithm performed particularly well, leaving close to 0 failure slices on average. Regularization scaling values of $$$10^3$$$ and greater produced few voids but over-regularized solutions, resulting in $$$|B_1^+|$$$ profiles with large CoV's independent of minibatch size. Figure 4 compares the different RF shimming algorithms in terms of $$$|B_1^+|$$$ CoV and average number of failure slices in the axial plane. Figure 5 shows example 8 channel shim magnitude profiles in one simulated head for singular vector minibatched GS versus conventional GS, with $$$s=$$$10, the same random initialization for both, and $$$k=$$$3.

Discussion and Conclusion

Our results show that a singular vector minibatching approach to GS-MLS shimming can robustly produce homogeneous shims with fewer shim-invalidating voids. While good initialization can produce a near-hole-free shim even with conventional GS, as indicated by the close performance of GS and minibatched GS when initialized with a CP-drive shim (Figure 2), the proposed algorithm is more likely to find a void-free solution regardless of initialization. The simplicity of the algorithm is also attractive, in that it does not require constrained optimization, and could be easily adapted to other pulse design problems such as spokes and $$$k_T$$$-points.

Acknowledgements

This work was supported by NIH grant R01 EB016695.

References

1. Setsompop K, Wald LL, Alagappan V, Gagoski BA, Adalsteinsson E.Magnitude least squares optimization for parallel radio frequencyexcitation design demonstrated at 7 Tesla With Eight Channels. Magn Reson Med. 2008;59(4):908-915.

2. Hoyos-Idrobo A, Weiss P, Massire A, Amadon A, Boulant N. On Variant Strategies To Solve the Magnitude Least Squares Optimization Problem In Parallel Transmission Pulse Design And Under Strict SAR and Power Constraints. IEEE TMI. 2014;33(3):739-748.

3. Zhang H, Zhou Y, Liang Y, Chi Y. A Nonconvex Approach for Phase Retrieval: Reshaped Wirtinger Flow and Incremental Algorithms. Journal of Machine Learning Research. 2017;18:1-35.

4. Monardo V, Li Y, Chi Y. Solving Quadratic Equations via Amplitude-based Nonconvex Optimization. IEEE ICASSP 2019;5526-5530.

5. Grissom W, Yip C, Zhang Z, Stenger A, Fessler J, Noll D. Spatial Domain Method for the Design of RF Pulses in Multicoil Parallel Excitation. Magn Reson Med. 2006;56(3):620-629.

6. Candes E, Li X, Soltanolkotabi M. Phase Retrieval via Wirtinger Flow: Theory and Algorithms. IEEE TIT. 2015;61(4):1985-2007.

7. Martin J, Ong F, Ma J, Tamir J, Lustig M, Grissom W. SigPy.RF:Comprehensive Open-Source RF Pulse Design Tools for Reproducible Research. (2020). Proc. of the Intl. Soc. Mag. Reson. Med. p 1045.

8. Fessler, J. Michigan Image Reconstruction Toolbox, available at https://web.eecs.umich.edu/~fessler/code/. Downloaded Nov 2019.

Figures

a) An example B₁⁺shim field designed using the conventional GS algorithm, with a large signal void in it. B₁⁺ maps are from a healthy volunteer on an 8 channel transmit system at 7T b) To help avoid signal voids, we propose the modified singular vector minibatched GS algorithm above, with the A singular vector sampling step shaded gray

Comparison of initialization schemes on an 8 channel (left plots) and 30 channel (right plots) transmit system. For each initializer, the results of the proposed algorithm are plotted on the left, and conventional GS is plotted on the right. The results for 30 channels are separated by shim orientation. The minibatched GS approach outperforms conventional GS void reduction in every geometry/initializer combo excluding CP/8ch/ax.

Parameter space of regularization factor s versus k with random initialization for an 8 channel (a) and 30 channel (b) system. Average number of shimming failures per head is shown in the left column, and average slice B₁⁺ CoV is shown in the right column. Note that the far right column in each plot corresponds to a full-rank A, equivalent to conventional GS. Using random low-rank approximations in the initial minibatched stage produced fewer voids than full-rank conventional GS when less than approximately 2/3 of the SVD components were kept.

Comparison of shimming techniques in an axial geometry on 8 channel and 30 channel systems. The singular vector minibatching GS approach produced the lowest CoV and the fewest failure slices of any method aside from CP drive in the 8 channel case, which is a void-free but high-CoV solution.

Example magnitude shims for an 8 channel coil with random shim initialization for each slice. (L) The conventional Gerchberg-Saxton algorithm produces a large number of failure slices with signal voids, (R) our two-stage GS algorithm produces no holes. Plotted using the MIRT⁸.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

3339