Introduction

High-Temperature Superconducting (HTS) radiofrequency (RF) coils can greatly improve the sensitivity of MRI, with Signal to Noise Ratios (SNRs) increased by more than an order of magnitude¹. A possible complication of using this technology is the B₀ inhomogeneity induced by dc magnetic flux expulsion, also known as superconducting diamagnetism. In the presence of a magnetic field, HTS materials generate screening currents on their surfaces/egdes, whose magnitude and distribution strongly depend on the temperature and magnetic history of the superconductor, notably whether it was cooled in the presence (field cooled) or the absence (zero-field cooled) of a magnetic field. So far, HTS coils have commonly been used at LN2 temperature, i.e. sufficiently close to the superconducting transition temperature T_c of the HTS material for such artefacts to have been (fortuitously) avoided. However, with better-controlled experimental parameters and new cryostats achieving lower temperatures, this becomes an issue. We report on the first observation of B₀ artefacts generated by HTS coil diamagnetism². We study these effects as a function of temperature and for different cooling conditions. We propose a phenomenological model reproducing the artefacts observed in the phase images, and we describe how they can be avoided.

Material and Methods

The equipment used for this experiment is shown in Figure 1. The cryostat³ is MRI compatible and can attain a minimal temperature of ~ 60 K (Figure 1b). The MRI system is a clinical 1.5 T set-up (Philips, The Netherlands). A whole-body RF coil was used for transmission/reception, and the MRI sequence was a standard 3D gradient-echo. The phantom is a cylinder of diameter 50 mm centered on the position of the HTS coil, on top of the cryostat (Figure 1a.b). The coil design is a 14.4 mm multi-turn Transmission Line Resonator⁴ (MTLR): a pair of six-turn YBa₂Cu₃O_7-δ spirals (T_c = 86 K) on both sides of a Al₂O₃ substrate. For this experiment, we used a non-resonant antenna (Figure 1c) so as to avoid B₁ artefacts while keeping intact the diamagnetic response of the HTS material. 3D MR images were acquired after zero-field cooling (outside the MRI scanner), field cooling (inside the MRI scanner) and for different temperatures varying from 60 K to 90 K.

Results

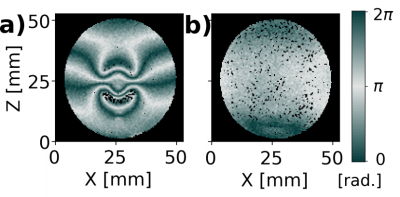
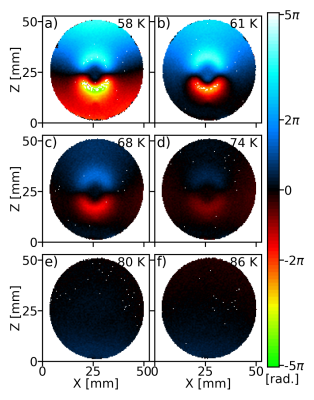
In Figure 2, we present two phase images in a coronal plane located 4.2 mm away from the HTS coil. The image in Figure 2a was acquired after zero-field cooling. We observe signal loss and important perturbations in the phase image. These anisotropic artefacts are minimal toward y ( $$$\perp\vec{B}_0$$$) and maximal toward z ($$$\parallel\vec{B}_0$$$). The image in Figure 2c was acquired after field cooling. The image is free of artefacts. In Figure 3, we present the results of the temperature study after zero-field cooling. The phase data were unwrapped⁵. The B₀ artefacts show a strong dependence on temperature; the shape and size of the phase pattern do not change, but the amplitude is continuously reduced as the temperature increases, up to the point where it becomes almost unnoticeable at 74 K (Figure 3e) and nonexistent at T > 80 K (Figure 3f).

Model

The B₀ artefacts observed in the phase images can be reproduced with a simple phenomenological model of the diamagnetism of the HTS coil. This model uses the coil geometry and computes the magnetic field $$$\vec{\Delta B}=I_0\vec{\Delta b}$$$ generated by an in-plane screening current I₀ circulating around the coil perimeter. The phase $$$\phi$$$ at position $$$\vec{r}$$$ is expressed as :

$$$\phi(\vec r,T)=\gamma T_EI_0\Delta b_z(\vec{r},\vec{r}_0)+\phi_0(T)+\vec{\phi}_r\cdot\vec{r},\quad(1)$$$

where $$$\Delta b_z$$$ is the z-component of $$$\Delta\vec{b}$$$, $$$\vec{r}_0$$$ is the position of the antenna relative to the sample, $$$\gamma$$$ is the gyromagnetic ratio of the proton, $$$T_E$$$ is the echo time, and $$$\phi_0$$$, $$$\vec\phi_r=[\phi_x,\phi_y,\phi_z]$$$ and $$$I_0$$$ are fitting parameters determined by linear regression for each temperature.

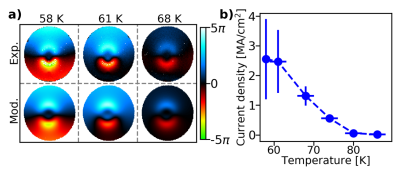
Experimental and modelled phase images displayed in Figure 4a are in good agreement. At 80 K, the field inhomogeneities attain 0.16 ppm in the phantom, whereas they attain 6.6 ppm at 58 K. This generates a field gradient of ~ 8 mT/m (at 58 K), inducing a phase drift of ~1.4 $$$\pi$$$ over a single voxel, ultimately leading to signal loss. From the current $$$I_0(T)$$$, we estimate the screening current density $$$j$$$ in the YBa₂Cu₃O_7-δ strip (Figure 4b). We find that $$$j$$$ ~ 2.6 MA/cm² at 58 K decreasing to $$$j$$$ ~ 0.4 MA/cm² at 77 K. This tracks the temperature dependence of the HTS coil critical current density⁶ $$$j_c$$$.

Conclusions

B₀ artefact arising from superconducting diamagnetism in HTS coil can severely degrade image quality in MRI. However, this can be avoided by either working at temperatures close to T_c, or by field cooling the HTS coil inside the MRI scanner. This work studies and solves an important issue in the implementation of HTS coil and provides better understanding of the experimental conditions required to obtain better images with this technology.

Acknowledgements

Experiments were performed on the 1.5 T MRI platform of CEA/SHFJ, affiliated to the France Life Imaging network and partially funded by the network (grant ANR-11-INBS-0006).