3329
The Spherical Harmonic Rating: A Metric for B0 Shim System Performance Assessment1Université Paris-Saclay, CEA, CNRS, BAOBAB, NeuroSpin, Gif-sur-Yvette, France
Synopsis
Different B0 shim system designs are tested on two distinct fieldmap databases for assessment of commonly employed metrics for evaluation of B0 inhomogeneity mitigation. We verify that those metrics might not always be the best choice for performance analysis, as, for a same shim system, they may provide hardly comparable values across sites. We then propose a novel, simple and robust metric for shim system analysis, the Spherical Harmonic Rating, which is shown to provide consistent performance across sites, providing an equivalency of the shim system to a Spherical Harmonics basis.
Introduction
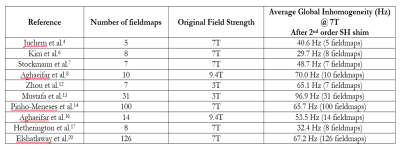
As MRI scanners move to Ultra-High Field (UHF), B0 inhomogeneity in the human brain increases proportionally, notably exacerbating geometric distortion and signal loss in Echo Planar Imaging (EPI). To reduce such artifacts, a significant amount of work has been done by several research groups to design B0 shim systems capable of pushing the boundaries of inhomogeneity mitigation1-19 relatively to conventional 2nd/3rd order Spherical Harmonics (SH) shimming, integrated in commercial scanners.The widespread metric for evaluating B0 inhomogeneity is the standard deviation of the magnetic field excursion ($$$\sigma_{\delta{}B_0}$$$) across voxels in the region of interest. However, significant variability of this metric across different sites even at the same B0 field strength has been observed7,12, making it insufficient for assessment and comparison of performance of different shim systems across research sites. Examples of baseline inhomogeneity reported by different sites at different field strengths are shown in Figure 1, with cases of strong variability even at a same site at the same field strength. Noise, different brain mask topology and fieldmap estimation method, for instance, have been hypothesized as potential sources of noticed variability12, but the question remains open.
To overcome this difficulty, we propose a simple and robust metric denominated Spherical Harmonic Rating (SHR), which is based on a quantitative comparison of the proposed shim system to SH-based systems.
Methods
For a given fieldmap, if the resulting inhomogeneity $$$\sigma_\text{shim}$$$ after shimming by some arbitrary system is between that obtained by unconstrained SH shimming of orders $$$n$$$ and $$$n+1$$$ ($$$\sigma_{\text{SH}_n}\geq{}\sigma_{\text{shim}}>\sigma_{\text{SH}_{n+1}}$$$), the SHR of such system for this particular fieldmap is given by:$$SHR=n+\frac{\sigma_{\text{SH}_n}-\sigma_{\text{shim}}}{\sigma_{\text{SH}_n}-\sigma_{\text{SH}_{n+1}}}$$
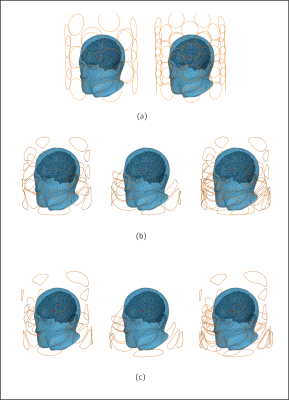
To verify consistency of this metric across different sites, an in-house database15 composed of 100 fieldmaps, acquired at 3T and re-scaled to 7T, and an open-access database20 with 126 fieldmaps, at 7T, are used in shimming simulations, first with two different matrix Multi-Coil Arrays (M-MCAs) (cf. Fig. 2a), of 24 and 48 channels. The M-MCAs are composed of regularly distributed circular loops around a cylindrical surface of 300-mm length and 281-mm diameter. The uniform coverage of the cylindrical surface by these generic designs should provide an unbiased system, delivering similar performance across distinct databases.
In addition, two 2-layer 36-channel optimized MCAs (Fig. 2b and c) designed using a SVD-based methodology10,15 are simulated and evaluated using the SHR. A low-bias and a high-bias SVD-based MCA system (S-MCA) with respect to the in-house database were designed based on 50 and 100 fieldmaps, respectively. Besides using only 50 subjects, relaxed field-error tolerance was allowed in the low-bias S-MCA design.
All shim systems are simulated over both databases considering coils with 20 wire turns and maximum 3A per channel.
Average baseline inhomogeneity across fieldmaps of the in-house and open-access database are 65.7-Hz and 67.2-Hz, respectively.
The SHR is compared to the inhomogeneity metric and to relative improvement over baseline inhomogeneity.
Results and Discussion
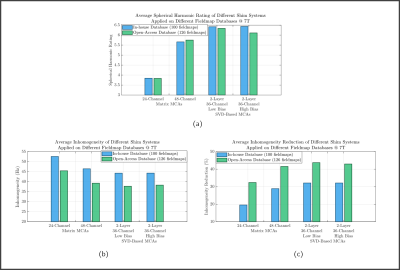
From results in Fig. 3b and c, assessment of the MCAs’ robustness across sites from inhomogeneity and inhomogeneity reduction metrics is not evident. Considerable metric differences across databases for each MCA are observed. An exact same M-MCA would appear to present over 10% absolute difference in inhomogeneity reduction when used on different sites at the same magnetic field and electric current constraints, despite the different databases presenting similar values of baseline inhomogeneity.The differences considering the inhomogeneity metric are also large, circa 7Hz. However, although the variability in this metric makes it unsuitable for comparison of performances, it is the standard metric for inhomogeneity assessment and it presents valuable information regarding the magnetic field in the Region-of-Interest.
The average SHR for the different systems is shown in Figure 3a. From this metric, M-MCAs seem to provide practically the same performances across different databases, which is expected for these generic designs. This evidences the invariant characteristic of the proposed metric. The 24 and 48-channel M-MCAs present a SHR difference between databases of 0.01 and 0.09, respectively. For S-MCAs, we see that the low-bias system behaves similarly to a 48-channel M-MCA in terms of robustness to inter-subject variability, with difference in SHR across databases of 0.09. For the high-bias S-MCA, the difference is 0.33, clearly indicating its reduced robustness, as the difference is 3.7 times greater than for the low-bias design. Therefore, the SHR easily highlights drop in performance of the high-bias S-MCA on the OA database relatively to the in-house database.
Conclusion
The SHR provides numerical values consistent with the expected behavior of the different shim systems.Certainly, although providing consistent values across different databases for a same shim system, the SHR alone does not provide all the information needed for assessing the expected image quality from some acquisition, and observing the field excursion values across different slices and the global inhomogeneity is necessary.
Nevertheless, to aid clinicians and researchers to pick their shim system from the many designs available in the literature, this metric could be helpful and we encourage its use; or that comparisons between the inhomogeneity obtained by the shim system design and what would be achieved with unconstrained SH shim systems are provided. Therefore, using a common basis for analysis, consistent across sites.
Acknowledgements
No acknowledgement found.References
1. C. Juchem et al. Dynamic multi-coil shimming of the human brain at 7T. Journal of Magnetic Resonance 2011; 212(2):280–288.
2. J.W. Pan et al. Role of Very High Order and Degree B0 Shimming for Spectroscopy Imaging of the Human Brain at 7 Tesla. Magn. Reson. Med. 2012; 68:1007-1017.
3. H. Han et al. Integrated parallel reception, excitation, and shimming (iPRES). Magn. Reson. Med. 2013; 70(1):241–247.
4. C. Juchem et al. Dynamic multi-coil technique (DYNAMITE) shimming for echo-planar imaging of the human brain at 7 Tesla. NeuroImage 2015; 105:462–472.
5. J. P. Stockmann et al. A 32-channel combined RF and B0 shim array for 3T brain imaging. Magn. Reson. Med. 2016; 75(1):441–451.
6. T. Kim et al. Gradient-Echo EPI Using a High-Degree Shim Insert Coil at 7 T: Implications for BOLD fMRI. Magn. Reson. Med. 2017; 78:1734-1745.
7. J.P. Stockmann, and L.L. Wald. In vivo B0field shimming methods for MRI at 7 T. NeuroImage 2018. 168:71-87.
8. A. Aghaeifar et al. Dynamic B0 shimming of the human brain at 9.4 T with a 16-channel multi-coil shim setup. Magn. Reson. Med. 2018; 80(4):1714–1725.
9. B. Pinho-Meneses and A. Amadon. A novel few-channel coil design for human brain shimming based on stream function Singular Value Decomposition. Proc. ISMRM 2019; p.1483.
10. B. Pinho-Meneses, M. Luong, and A. Amadon. Optimized multi-coil array design for human brain shimming at Ultra-High Field. Proc. ISMRM 2019; p.1477.
11. B. Pinho-Meneses and A. Amadon. Static-magnetic-field shimming coil system for magnetic resonance imaging. European Patent 072081EP/EPR 2019.
12. J. Zhou et al. An orthogonal shim coil for 3T brain imaging. Magn. Reson. Med. 2019; 83:1499-1511.
13. M.C. Can et al. Designs of shim coils with distributed currents for 3T human brain magnetic resonance imaging. Proc. ISMRM 2019; p. 1471.
14. B. Pinho-Meneses, and A. Amadon. A fieldmap-driven few-channel shim coil design for MRI of the human brain. Phys. Med. Bio. 2020.
15. B. Pinho-Meneses et al. First prototype of a Stream-Function-based Multi-Coil Array dedicated to human brain shimming at Ultra-High-Field. Proc. ISMRM 2020; p.766.
16. A. Aghaeifar et al. A 32-channel multi-coil setup optimized for human brain shimming at 9.4T. Magn. Reson. Med. 2020; 83:749-764.
17. H.P. Hetherington et al. Dynamic B0 shimming for multiband imaging using high order spherical harmonic shims. Magn. Reson. Med. 2020; 85:531-543.
18. C. Oh, E. Choi, W. Hung, and J. Lee. Machine designing: a multi-coil local shim design using Bayesian optimization. Proc. ISMRM 2020; p. 4227.
19. N. Arango et al. Computational Shim Coil Design Applied to Augmenting a Shim Array with a Non-Eye-Occluding Face Plate. Proc. ISMRM 2020; p.4224.
20. H. Elshatlaway et al. An open dataset of 126 human brain field maps. Proc. ISMRM 2020; p. 4219.
Figures