Introduction

Thigh muscle morphology and composition quantified from MRI have been suggested as potential imaging biomarkers for multiple diseases including osteoarthritis and sarcopenia. To obtain reliable quantification of either morphology (e.g., area or volume) or composition (e.g., fat fraction), robust and fast segmentation techniques are desirable. The thigh muscle is composed of tightly bundled muscle groups that have similar intensities in MR images. Semantic segmentation of individual muscle groups is therefore challenging due to the lack of clear boundaries between different muscle groups. Pure intensity-based segmentation approaches¹ can separate the entirety of the muscle tissue from the background, but usually fail to separate one muscle group from another. Not much work has been performed in this direction. There are several existing fully automatic thigh muscle segmentation methods that are based on deep learning^2,3 which require large data sets and extensive computational time for training. We provide a semi-automatic non-learning based scheme with an average Dice coefficient of 92.5%.

Methods

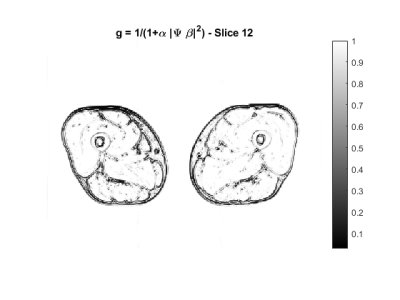
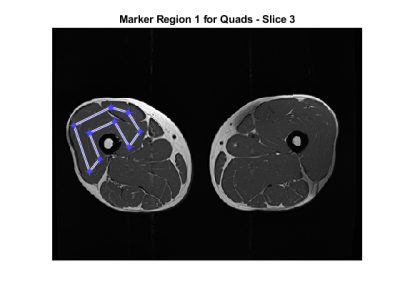
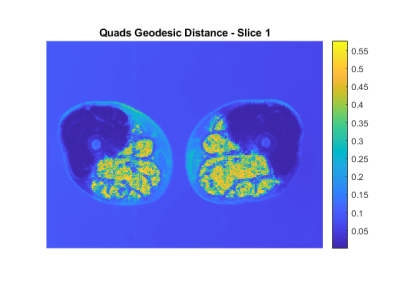
Let $$$u$$$ be the image to be segmented. We segment each muscle group separately. Our method requires two inputs from the user: a set of marker points inside the muscle group and a set of anti-markers that are near, but just outside of the muscle boundary. We use geometric flow to evolve the markers toward the boundary of the muscle group. The evolving curve is called active contour. We represent the evolving contour using the zero level set of a function $$$\phi$$$ to allow for flexible changes in topology. The geometric flow that updates the contour is $$$\frac{d\phi}{dx} = (F + q \kappa) |\nabla \phi|$$$ where $$$F$$$ is an evolving force that controls the speed and direction of the geometric flow, $$$\kappa$$$ is the curvature, and $$$q>0$$$ is a balancing factor that controls the smoothness of the contour. To stop the evolution of the curve at the boundaries, we rely on an effective force $$$F$$$. Typically, the force $$$F$$$ is based on the image gradient, but it does not work well in segmenting closely bundled muscle groups since the boundaries between them are not always clear and distinct. We design a novel force function $$$F = g - \gamma D_p - \eta c$$$ that is based on three elements: 1) $$$g$$$, a better edge stopping function that stops the contour evolution at the edges; 2) $$$D_p$$$, a geodesic distance based term that ensures the final contour is near the markers but away from the anti-markers; 3) $$$c$$$, the average intensity of voxels inside the markers. For $$$g$$$, we use the edge descriptor $$$\Psi\beta$$$ from our previous work⁴: it is large for edges and small for homogeneous regions. As an edge stopping function, $$$g = \frac{1}{1+\alpha|\Psi\beta|^2}$$$ works better than gradient. For $$$D_p$$$, we first calculate the geodesic distances to $$$M$$$ and $$$AM$$$ , denoted by $$$D_M, D_{AM}$$$ respectively, by computing the viscosity solution $$$D(x,y) \geq 0$$$ to the Eikonal equations $$$|\nabla D(x,y)| = \epsilon + \tau |\Psi \beta|$$$ using fast sweeping method⁵ with the condition $$$D(x,y) = 0$$$ on $$$M$$$ and $$$AM$$$ respectively⁶. $$$D_p$$$ is the average of $$$D_M$$$ and a function of $$$D_{AM}$$$ that is reversely proportional to $$$D_{AM}$$$. The third element involves the mean value of the voxels inside the markers. It avoids overshooting by dragging the contour inward when it passes over the boundary. Note the force $$$F$$$ can be negative and causes the active contour to evolve inwards to fix overshooting.

We tested the algorithm on MRI data collected from two subjects (one female 30y; one male 49y) using a 3T MRI scanner (SkyraFit, Siemens) with an 18-channel flex coil: TR/TE = 795/10 (ms), an FOV of 400x312x140 mm³, and the image size is 511x383x28. The image intensity was first normalized to [0,1] and the parameters are: $$$q=0.3, \gamma = \eta = 10, \alpha = 10^3, \epsilon = 0.1, \tau = 10^3.$$$ Dice similarity coefficients were calculated using manual segmentation as reference.

Results

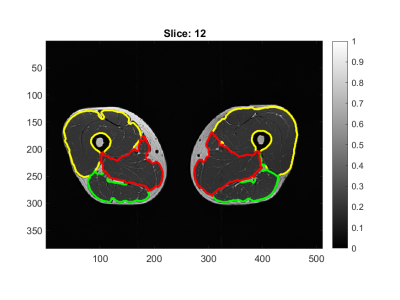
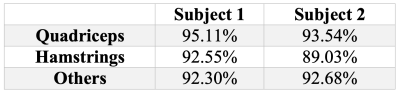
In Figure 1 an example of the $$$g$$$ map is illustrated. In Figure 2 we superimpose markers on the left quadriceps of a raw image slice, and the geodesic term $$$D_p$$$ is shown in Figure 3. We can see that $$$D_p$$$ is close to zero inside the quadriceps but is larger in the surrounding muscle groups. The segmentation of three muscle groups (quadriceps, hamstrings, and others) on one slice is shown in Figure 4. The Dice coefficients from the two subjects are listed in Table 1. The average Dice coefficient was 92.5%.

Discussion

In this study, we developed a novel semi-automatic technique for segmenting different muscle groups from MRI images. The only user inputs required for the proposed scheme are the markers and anti-markers. We can, however, make it completely automatic by obtaining markers and anti-markers through other methods. For instance, registering from an atlas is an efficient way to get preliminary segmentation results that can be adapted to serve as markers and anti-markers.

Conclusions

The proposed active contour based semantic MR muscle segmentation method is very effective at segmenting MR muscle groups that are tightly bundled together. It has the potential to be applied to thigh muscle morphology and composition quantification from MRI.

Acknowledgements

The study was supported by NIH/NIAMS AR075422.