Introduction

Eddy currents induce localized magnetic fields that oppose the original field, distorting the image¹. Such issues are particularly prominent in DTMRI measurements due to the common use of echo-planar imaging (EPI) and the need for rapid gradient switching. Eddy current correction is useful in analysis of neuronal DTMRI data. Although it is recognized that there are distinct requirements of neuronal and muscular DTMRI studies, the effect of eddy current correction on muscle diffusion measurements has not been systematically investigated. The purpose of this work is to preliminarily evaluate eddy current correction on muscle diffusion measurements by comparing the image morphology and diffusion tensor indices derived from diffusion tensor with and without eddy current correction.

Methods

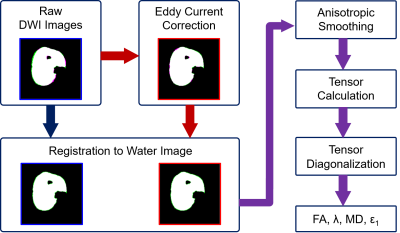
Data acquisition: Imaging was performed using a 3T MRI system (Philips, Elition; Best, The Netherlands) with 16 channel surface-receive coil and 8 table top coils. Data were acquired in the right leg of 7 young healthy participants with the foot fixed in 20° of dorsiflexion. Diffusion-weighted imaging used pulse-gradient spin-echo-EPI using: 24 diffusion-encoding directions with b=450mm²/s; TR/TE, 5300/53ms; NEX, 4; acquisition voxel size 2×2×7 mm; reconstructed voxel size 1×1×7 mm; and olefinic signal saturation, aliphatic signal inversion, and slice-selective gradient reversal for fat signal suppression. Non-diffusion-weighted images were acquired at opposite phase-encoding directions with b=0mm²/s, with all other parameters the same. 3D quantitative fat/water MR images (6 echoes with TR/TE/ΔTE 210/1.01/0.96ms) were used for anatomical reference.

Data preprocessing: Imaging data were converted to NIfTI format using dcm2niix² for further analysis. Figure 1 depicts the workflow and illustrates the method for characterizing the morphological mismatch between diffusion-weighted images and anatomical images. Eddy current correction was performed on diffusion-weighted imaging data using FSL^3,4. Then a target slice was selected at the approximate location of the largest cross-sectional area of the leg. Masks were generated on anatomical and diffusion-weighted images at the selected slice through semi-automatic segmentation using MATLAB’s built-in function activecontour, followed by manual removal of areas of skin and bones. Masks for the whole tibialis anterior muscle and its superficial and deep compartments were manually created using the anatomical images, with tendon tissue masked out. Registration of diffusion-weighted images to the anatomical image used MATLAB’s imregdemons function. Calculation of diffusion tensors used a weighted least squares approach. Maps of fractional anisotropy (FA), eigenvectors (ε₁, ε₂ and ε₃), eigenvalues (λ₁, λ₂, λ₃) and mean diffusivity (MD) were formed using custom-written MATLAB routines.

Morphological comparison of masks: Morphologies of masks covering the whole cross-sectional area on unregistered diffusion-weighted images, before and after eddy-current correction, were compared with an anatomical image mask. Fractions of the number of mismatching pixels in the total pixel number of anatomical masks were calculated. Paired t-tests were performed at significance level of 0.05 to determine whether eddy current correction improved the morphological match between the masks on diffusion weighted image and on anatomical image.

Comparison of FA, eigenvalues and MD: Maps for FA, eigenvalues and MD within tibialis anterior muscle were calculated. Mean values of FA, eigenvalues and MD across the whole tibialis anterior muscle and its standard deviation were calculated and compared.

Comparison of the distribution of the first eigenvector: The eigenvector corresponding to the largest eigenvalue at each voxel within tibialis anterior (ε₁) was extracted. Also, the mean direction of ε₁ was calculated using a diffusion tensor derived from the mean signal vector. Then, the angular deviations of each voxel’s ε_­1 vector from the mean direction were calculated. These analyses were performed separately for the superficial and deep compartments of the muscle. Standard deviations of angular deviations were calculated and compared for images analyzed with and without eddy current correction.

Results

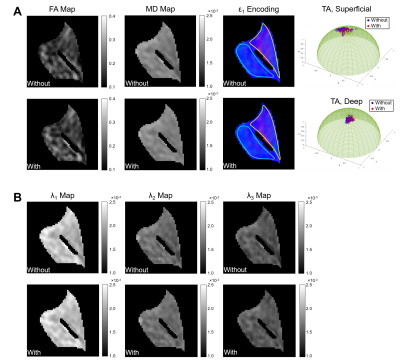
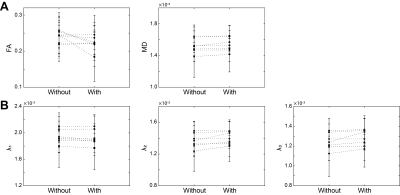
Eddy current correction reduced the fraction of mismatched mask pixels by an average of 1.76% (p=0.002). Figure 2 illustrates an example of comparison of derived indices from diffusion measurements in one subject. Figure 3 shows the changes in FA, eigenvalues, and MD that occurred when eddy current correction was included in the pre-processing pipeline. Eddy current correction resulted in an increase of the mean FA in three of the cases and decrease of the mean FA in the other four. The mean λ₁ value increased in four of the cases, while it decreased in the other three. The mean values of λ_­2 and λ₃ increased in all cases, and significance of change was observed at the level of 0.05 (p=0.024 and 0.048 for λ₂ and λ₃, respectively). The mean MD increased in all cases by a relatively small amount (0.26% - 3.42%), but these changes were not significant (p=0.16). The variability of ε₁ in the superficial compartment slightly decreased in three of the cases and increased in the other four. In the deep compartment, the variability of ε₁ decreased in two of the cases and increased in the other five.

Discussion & Conclusion

The eddy current correction helped correct the morphological distortions of muscle diffusion images, but did not convincingly improve the derived parameters from muscle diffusion measurements. Future investigations are needed to examine its effects on geometric properties of reconstructed muscle fibers based on DTI tractography and to evaluate the necessity of including eddy current correction in the analysis of other muscle groups.

Acknowledgements

The authors thank Dr. Kurt Schilling for the help in preprocessing of diffusion data.