Introduction

Large-scale neurocognitive networks continuously undergo reorganization. They are reflected as slowly varying BOLD signals in resting-state fMRI (rs-fMRI) networks (RSN) and as fast-transient microstates in EEG. The number of residual unknown clusters, instability of k-means and fuzzy methods account for the randomness in traditional EEG microstate analysis, thereby resulting in ambiguous topographical cluster boundaries.^1,2,3 In an attempt to overcome this shortcoming, we propose a novel and stable quantum mechanics based-clustering technique. Each data point, assumed to be generated from a quantum mechanical system, is allocated to the closest minimum value of potential V(x) by considering topographic EEG information to be discrete quantum potentials and isolating even smaller clusters by estimating the minimal potential points as cluster ^4,5 To validate our technique, the quantum microstates were further correlated with resting state-fMRI networks.

Methodology

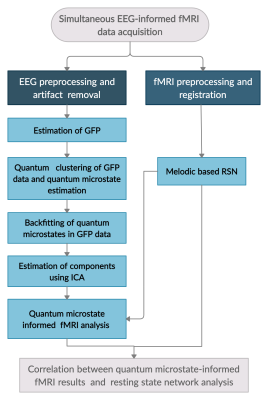
Simultaneous EEG-fMRI resting-state data of thirty-nine healthy volunteers (mean age: 19.57 ± 1.28 (SD) years) was acquired using a 3 Tesla MR scanner (Skyra, M/s Siemens) and a 32 channel MR compatible EEG system (Brain product, Germany). For EEG acquisition, electrodes were placed according to the standard 10–20 system with an impedance level <5 kΩ for each electrode and sampling frequency of 5000Hz. MR related artifacts in EEG data were cleaned using the average artifact subtraction algorithm (AAS) and then subjected to the HAPPE toolbox for removal of conventional EEG artifacts.⁶ The artifact removed EEG was referenced to the common average reference and Global field power (GFP) was evaluated (flowchart in Figure 1). Quantum clustering was performed on the GFP EEG data to estimate lowest eigenstates, that served as solutions to the time-independent Schrodinger equation,
$$H\psi\equiv(-{\sigma^{2}\nabla^{2} \over 2} + V(x)) \psi = E\psi$$
The first Lagrangian term is treated as a source of variance modulated by the Gaussian width $$$\sigma$$$ and the potential function V(x) for a set of closely located data points render themselves as a source of attraction. For a Parzen window approach, $$$\psi(x)$$$ serves as the probability density for generating each data point x_i . The wave function $$$\psi(x)$$$ with Gaussian width $$$\sigma$$$ was constructed from the EEG GFP data as $$$\psi(x) = \sum e^{(x-x_i)^2/(2\sigma^2)}$$$ and further the potential function was substituted by $$$V(x) = E + {\sigma^{2}\nabla^{2} (\psi)\over2\psi}$$$.
The estimated lowest eigenstates, are defined as the quantum cluster centers and thus called quantum microstates. This vector was used for EEG data of entire GFP data and the independent components of quantum microstate re-expressed GFP EEG data were identified using independent component analysis (ICA). The rs-fMRI data were preprocessed and subjected to the traditional melodic approach in FSL to estimate resting-state networks such as Default Mode (DMN), Fronto-Parietal (FP), Executive, Motor, Visual, Basal Ganglia (BG) networks. In order to assess the association of quantum microstate with rs-fMRI networks, each independent component of quantum microstates was independently subjected to EEG informed fMRI method and their neural correlates were estimated. The temporal correlation information of both neural correlates of independent components of quantum microstates and rs-fMRI networks was estimated.

Results

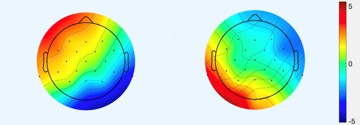
Quantum microstates were estimated by measuring the eigenstates, that served as global minima of potential function (Figure 2). Robust correlation between the time series information of ICA components (both quantum microstates) with the temporal series information of the resting-state fMRI networks (figure 3) was observed in the frontoparietal (IC1:-0.41, IC3:0.45, IC6:0.41), posterior DMN (IC2:0.42, IC5:-0.38), executive (IC4: -0.39, IC6: 0.39), visual (IC1: 0.42) and sensory-motor (IC6: 0.39) networks with p<0.01. The anterior DMN (IC1:0.34, IC3:-0.31, IC5:0.32) showed moderate correlation while basal ganglia revealed a reduced correlation with quantum microstate information.

Discussion

Resting-state analysis helps in understanding the dynamic and complex functional interactions between different brain regions, as part of large-scale neuronal communication, based on very slow hemodynamic and fast electrical information. The proposed quantum microstates revealed a good correlation with slow and stable rs-fMRI networks. Strong cross-correlations observed between the different ICs of quantum microstates and rs-fMRI network indicates that the neuronal assemblies of the different nodes of the fMRI RSNs interact with each other at smaller time scales. This reveals that EEG microstates are influenced by a network of approximately simultaneously active neural sources.¹

Conclusion

The proposed quantum microstate approach revealed its ability in explaining the sub-second coherent neural activation within global large-scale functional brain networks. The proposed microstate exhibited a very strong and significant correlation with functional networks.

Acknowledgements

This study was supported by the Defence Research and Development Organisation, India.