3140
Group cohesive parcellation results in superior functional-based parcellation with greater parcel-level parsimony than current approaches1Cleveland Clinic, Cleveland, OH, United States
Synopsis
Cohesive parcellation aims to produce parcels whose member voxels highly correlate to the parcel’s mean (exemplar) time series. The previously presented single subject version of cohesive parcellation is improved and extended to the group level using a novel hybrid parallel hierarchical framework. The resulting group parcellation compares favorably to traditional anatomical and connectivity-based parcellations over several measures of cluster validity at both the group level and when projected to individual subjects.
Introduction
Parcellation of the brain is a fundamental preprocessing step in network analysis of rsfMRI, after which an exemplar (typically the mean time course of member voxels) is extracted from each parcel and used for subsequent analyses1,2. While several methods exist to parcellate the brain, we previously introduced an approach that produced optimal parcel exemplars, termed cohesive parcellation3. This approach used cohesion (the average correlation between a parcel’s exemplar and its member voxels) as a linkage criterion in a spatial adjacency-constrained, agglomerative hierarchical clustering framework. Here, we improve and extend this single subject approach to the group level using a novel hybrid parallel framework, producing parcels ideal for downstream network analysis at the group level.Methods
Task-free fMRI was performed on 18 healthy adults with a Siemens Magnetom 7T (Siemens Medical Solutions, Erlangen, Germany) using a 32-channel receive coil (Nova Medical, MA, USA). Whole brain rsfMRI data were acquired using multi-band EPI with 81 contiguous 1.5 mm thick axial slices (MB factor = 3, TE/TR = 21/2800 ms, 128 volumes, 70° flip, 1602 matrix, 192 mm2 FOV, 1.2x1.2x1.5 mm3 resolution). High resolution T1-weighted images were acquired for anatomical context. rsfMRI data were corrected for slice timing, motion, and physiologically based nuisances4,5. Anatomical data was registered to both their corresponding functional data and a 1.5 mm3 isotropic MNI template. All data were then warped to this common space and smoothed (isotropic 2 mm FWHM Gaussian kernel) for group parcellation.Previously, we defined parcel cohesion at the single-subject level as the mean temporal correlation between the parcel exemplar and its member voxels and used this as the linkage criteria in a spatial adjacency-constrained, agglomerative hierarchical clustering framework3. In order to prevent bias towards larger parcels, we introduce a penalty term based on the correlation of the parcel exemplars themselves. For group parcellation, we utilize a framework where each subject’s data are clustered in parallel. Briefly, at each agglomeration step, we calculate linkage (cohesion) costs for each subject individually, and then pool them together to determine which two clusters to merge. We use the 10th percentile of this pooled cohesion as a robust linkage criterion that balances group cohesion with individual differences. The same group-optimal pair of clusters is merged for each subject, and the process is repeated until the full group hierarchical tree is determined. The final group parcellation is created by cutting this tree at a parcel cohesion threshold of 0.5.
Results
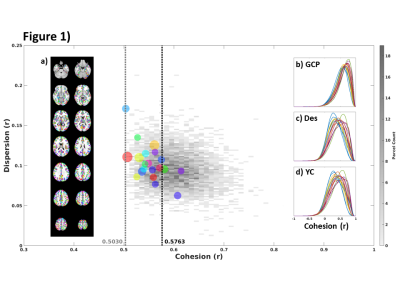
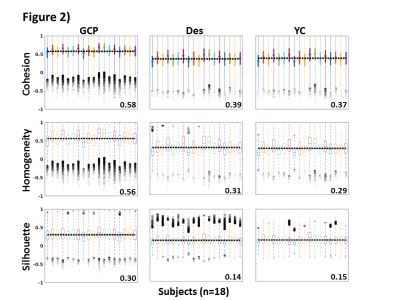
Figure 1 shows the distribution of the group average parcel cohesion using the proposed group extension to cohesive parcellation. The corresponding spatial map of the parcellation is also shown (a), which produced 4,717 parcels from 189,596 voxels. The size-weighed mean of group parcel cohesion was 0.58, and all parcels had cohesion greater than 0.5 as expected. Also shown are the underlying voxel-wise distributions of cohesion as a result of applying this group parcellation to each subject’s data (b). For comparison, the same distributions of voxel-wise cohesion are shown for traditional anatomical6 (c, Destrieux) and connectivity-based7,8 parcellations (d, Yeo/Choi). Figure 2 summarizes the results of various cluster validation measures on these parcellations. For each subject, the distribution of parcel cohesion (top row), homogeneity (middle row), and modified silhouette coefficient (bottom row) are shown for group cohesive parcellation (left column), anatomical parcellation (middle column), and traditional connectivity-based parcellation (right column).Discussion
Group cohesive parcellation produced a 40.2 fold compression of the data, which represents a substantial reduction, but not to the extent of previously published parcellations1,9. This group parcellation produces excellent parcel cohesion while preserving voxel-wise cohesion when projected to individual data. Group cohesive parcellation also compares favorably to traditional anatomical and connectivity-based parcellations for both cohesion and traditional measures of cluster validity. Homogeneity and silhouette coefficients for traditional parcellations match previously published values for our cohort of 18 subjects9.Conclusion
We present a group extension to cohesive parcellation that reduces the data burden for group rsfMRI connectivity and network analyses. The resulting parcels generate exemplars that are internally coherent with their underlying members at both the group and individual level, unlike all other current parcellations. Group cohesive parcellation even compares favorably using traditional methods of cluster validity, despite optimizing on non-traditional criteria. The current approach produces parcels that are easily interpretable for downstream analyses.Acknowledgements
Authors acknowledge technical support from Siemens Medical Solutions.References
1) Thirion B, et al. Which fMRI clustering gives good brain parcellations? Front Neurosci. 2014;167:1-13.
2) Eickhoff S, et al. Connectivity-based parcellation: critiques and implications. Hum Brain Mapp. 2015;36(12):5771-92.
3) Nemani A and Lowe MJ. Cohesive parcellation of rsfMRI using constrained hierarchical clustering. Proc 29th ISMRM. 2020;#3960.
4) Beall E. Adaptive cyclic physiologic noise modeling and correction in functional MRI. 2010;187(2):216-28.
5) Beall E and Lowe M. SimPACE: generating simulated motion corrupted BOLD data with synthetic-navigated acquisition for the development and evaluation of SLOMOCO: a new, highly effective slicewise motion correction. NeuroImage. 2014;101:21-34.
6) Destrieux C, et al. Automatic parcellation of the human cortical gyri and sulci using standard anatomical nomenclature. NeuroImag. 2010;53:1-15.
7) Yeo BT, et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J Neurophysiol. 2011;106(3):1125-65.
8) Choi EY, et al. The organization of the human striatum estimated by intrinsic functional connectivity. J Neurophysiol. 2012;108(8):2242-63.
9) Arslan S, et al. Human brain mapping: a systematic comparison of parcellation methods for the human cerebral cortex. NeuroImage. 2018;170:5-30.
Figures