Introduction

Brain’s number system is essential for humans to gauge magnitudes. Although people use numbers routinely, the process of generating the number in the brain has not been explicitly explained. Some think there are two core systems of numbering: approximate representations of numerical magnitude and precise representations of distinct individuals – counting and subitizing 1, whereas others prefer both functions sharing the same system 2. To resolve these arguments, an fMRI experiment was designed to quantitatively measure BOLD responses during the brain’s numbering processes. Based on the experimental data, a neural network model of subitizing and counting is established.

Experiment and Results

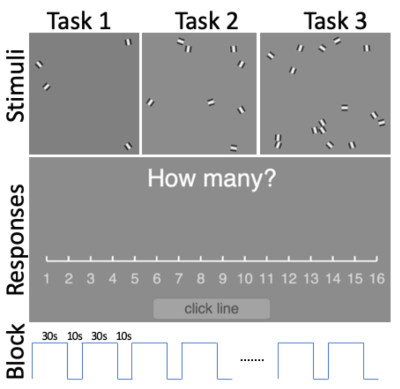
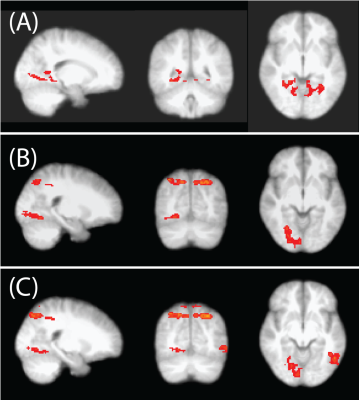
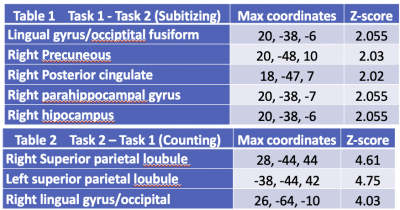
A total of 20 subjects participated in the fMRI experiment designed to distinguish human subitizing and counting processes. The cognitive stimulus adopts a mixed approach that combines both block and event-related designs. Each block consists of a 30s task and 10s fixation, as shown in Fig. 1. During the task period, a subject should either subitize or count the random numbers of dots on display. Once the number of dots is identified, they click the button on the track-ball, then the screen will be switched to a scale bar, they should move the cursor to the correct number on the scale with a track-ball, and click the button again to select the number. After selection, the display prompts another set of dots. There are three functional tasks in each study session, in which the numbers of the dots on the screen are 1-5, 5-9, and 10-16, respectively. The fMRI experiments are conducted on a Siemens 3T Prisma MRI scanner (Erlangen, Germany). The fMRI sequence is the product version of multi-band EPI, with TR 1s, TE 30ms, Flip angle 62, simultaneous multi-slice number 3, voxel size 3x3x3mm3, and volumes for each trial 400. The data processing uses the software package FSL’s FEAT (Oxford, UK).
The BOLD responses in each trial come from multiple stimuli, such as visualizing randomly distributed dots on a screen, subitizing/counting, using a trackball to select numbers on a scale, and clicking buttons. However, with statistical deductions from blocked and event-related datasets, the response for each stimulus can be derived. The most significant three results are A-B, B-A, and C-A, which correspond to subitizing > counting, short counting > subitizing, long counting > subitizing, respectively, as shown in Fig. 2; their corresponding MNI coordinates are in Fig. 3.

Neural Network Model

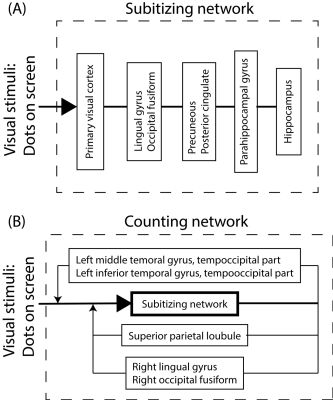
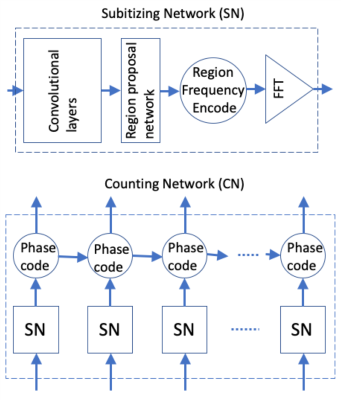
The heuristic assumptions are that subitizing is a parallel process that may be modeled by a region convolutional neural network (R-CNN or faster R-CNN for speed) 3; whereas counting is a series of subitizing facilitated by SPL, as well as T2/T3 for a long counting, which may be modeled by a recurrent neural network (RNN). The granger analysis estimated the hierarchical connectivity of Fig. 2, as shown in Fig. 4. Its corresponding deep-learning networks are shown in Fig. 5. Both the faster R-CNN and the RNN LSTM4 codes are implemented with the standard codes from Tensorflow (www.tensorflow.org). In the additional frequency and phase coding, the base frequency is set to 64Hz (gamma band); the modulation frequency for subitizing sampling is 10Hz (alpha band). If the object’s shape and texture in stimuli (Fig. 1) are trained, the success rate of this model is >95% for task 1 and >90% for task 3 in 500 tests.

Conclusion

An fMRI experiment elucidates a deep-learning network model for subitizing and counting. The underlying assumption is that subitizing is an essential module in counting, but its mechanism is different from counting. The best way to describe their relationship is that subitizing resembles a CNN, and counting is similar to an RNN where the subitizing is its recurrent cell. Further matching between the brain parcellates from fMRI data and the recurrent cell may reveal a number system at the large brain network level.

Acknowledgements

No acknowledgement found.