Introduction

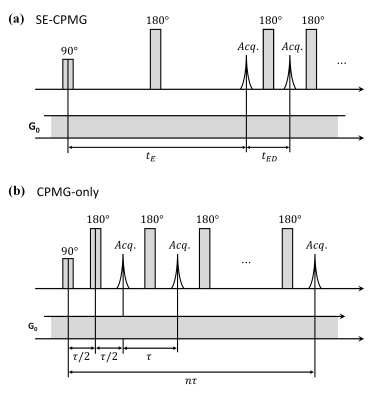
In single-sided NMR devices, reliable diffusion-relaxation (D-T₂) correlation measurement has become an important technique for the identification and clean separation of different components in heterogeneous tissues ^1,2, providing new opportunities for applications such as detection of liver steatosis ³.

In D-T₂ measurements, diffusion-editing CPMG (Carr-Purcell-Meiboom-Gill) sequence ^4-6 is commonly used. It consists of a preparation sequence (a spin-echo pulse pair in SE-CPMG ⁵, as shown in Fig. 1a) that encodes diffusion, followed by a long train of refocusing pulses (CPMG ⁷) that encodes relaxation. Recently, a new approach using the CPMG-only sequence for D-T₂ measurement is proposed (detailed in another abstract by our group). As shown in Fig. 1b, the diffusion-editing preparation is omitted. The CPMG-only sequence is less sensitive to motion and can extend to systems with more imperfect magnetic and radiofrequency (RF) fields.

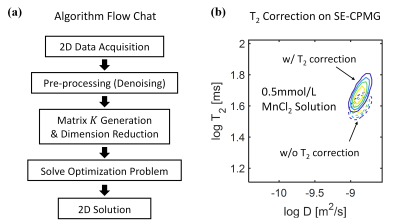
In this work, we validated the CPMG-only sequence by comparing it with the traditional SE-CPMG. The obtained D-T₂ results of different fluid samples (peanut oil, 0.5mmol/L MnCl₂ solution and their combination) were presented and discussed. A T₂ correction algorithm was also demonstrated which reduced the effect of self-diffusion during T₂ measurement for SE-CPMG.

Theory and Methods

Diffusion Encoding of the SE-CPMG and CPMG-only Sequences
The CPMG train is typically used to measure the transverse relaxation time T₂. Due to the presence of the static gradient in single-sided NMR, the echo time should be short enough to reduce the influence of molecular self-diffusion during T₂ measurement ⁵. However, in the CPMG-only sequence, we just make use of the diffusion effect during the CPMG train. Both diffusion and relaxation are encoded by the CPMG echo time τ , and the characteristic time decay of the echoes is ⁷
$$ S\left(n\tau\right)=Aexp\left(-\frac{1}{T_{2}}\cdot n\tau-\frac{\gamma^{2}G_{0}^{2}\cdot n\tau^{3}}{12}\cdot D\right) $$
On the other hand, for the conventional SE-CPMG sequence, diffusion is considered only encoded by the SE echo time t_E when the CPMG echo time t_ED is short enough
$$ S\left(nt_{ED}\right)=Aexp\left(-\frac{1}{T_{2}}\cdot nt_{ED}-\frac{\gamma^{2}G_{0}^{2}\cdot t_{E}^{3}}{12}\cdot D\right) $$
T₂ Correction for the SE-CPMG Sequence
In the SE-CPMG sequence with a strong static gradient strength, or for tissues with high diffusion coefficients, self-diffusion during the CPMG readout should not be neglected. The measured T₂ value is in fact shortened by a third term in the following equation:
$$S\left(nt_{ED}\right)=Aexp\left(-\frac{1}{T_{2}}\cdot nt_{ED}-\frac{\gamma^{2}G_{0}^{2}\cdot t_{E}^{3}}{12}\cdot D-\frac{\gamma^{2}G_{0}^{2}\cdot t_{ED}^{2}}{12}\cdot nt_{ED} \cdot D\right)$$
So a T₂ correction algorithm is proposed for more accurate D-T₂ measurement in SE-CPMG. The algorithm applied to the calculated D-T₂ map is expressed as
$$ \frac{1}{T_{2_{corr}}}=\frac{1}{T_{2}}-\frac{(\gamma G_{0}t_{ED})^{2}\cdot D}{12} $$
Materials and Methods
The experiments were performed using a specifically designed single-sided NMR device for detection of liver steatosis (Marvel Stone Healthcare, Wuxi, Jiangsu, China) as shown in Fig. 2. The mean strength of the magnetic field was 0.07 T, and the static gradient was 110 Gauss/cm.

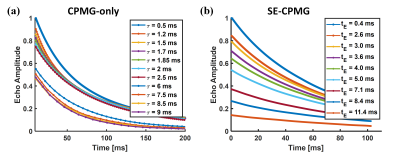
Aqueous MnCl₂ solution and commercial peanut oil were used in the experiments. TR (Repetition Time) was 1000ms and NSA (Number of Signal Averages) was 64 for both sequences. Fig. 3 showed the characteristics of the averaged signals measured from the two fluids (MnCl₂ solution and peanut oil) by the two sequences. The echo time τ (11 sets of τ for CPMG-only) and t_E (9 sets of t_E for SE-CPMG, t_ED=0.2ms) both covered a large scale so as to encode diffusion for either water (short echo time for high D value) or fat (long echo time for low D value).

To obtain the D-T₂ distribution functions, the inversion of the measured 2D NMR data was translated into an optimization problem ⁸, and L2 regularization was implemented. The data processing procedure for the SE-CPMG and CPMG-only sequences was identical and illustrated in flow chat (Fig. 4a). More details were explained in another abstract.

Results

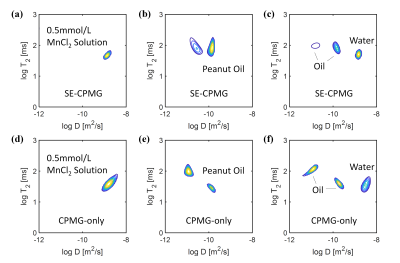
Fig. 5 shows the D-T₂ correlation maps acquired by the SE-CPMG (top row) and CPMG-only (bottom row) sequences, including results of the 0.5mmol/L MnCl₂ solution (a, d), the peanut oil (b, e), and their combination (c, f).

The two sequences present identical D-T₂ distributions of the 0.5mmol/L MnCl₂ solution, while show differences on the D-T₂ maps of the peanut oil, especially on the peak values. Despite the differences, both methods reveal the existence of the three main peaks of the two fluids, and the peak positions are close to the results of their single-fluid (peanut oil or MnCl₂ solution) experiments.

Discussion

The difference in the D-T₂ distribution between the two sequences is possibly introduced by the inconsistent positioning of the bottles in the experiments. Besides, it may result from the different encoding patterns of the two sequences. CPMG-only provides a more flexible encoding pattern, with the varying parameters n and τ.

We will conduct in-vivo (human liver) experiments in the future to evaluate the two sequences under respiratory movement. The CPMG-only sequence is less sensitive to motion because different b-values (encoded by nτ³) are added within the train. On the other hand, motion between the different b-values of the multiple t_Es in SE-CPMG may influence the measuring accuracy.

Conclusion

In conclusion, the CPMG-only sequence provides an alternative approach for the D-T₂ distribution measurement. It is easy to operate in the single-sided NMR device (for detection of liver steatosis) and can achieve comparable performance with the traditional SE-CPMG on water-fat separation.

Acknowledgements