3098
Design of Biplanar Matrix Z2 Nonlinear Gradient Coil with An Open Structure for O-Space imaging
Congcong Liu1,2, Shi Su1, Ye Li1,2, Xin Liu1,2, Hairong Zheng1,2, Dong Liang1,2,3, and Haifeng Wang1,2
1Paul C. Lauterbur Research Center for Biomedical Imaging, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, 2Shenzhen College of Advanced Technology, University of Chinese Academy of Sciences, Shenzhen, China, 3Research Center for Medical AI, Shenzhen Institute of Advanced Technology,Chinese Academy of Sciences, Shenzhen, China
1Paul C. Lauterbur Research Center for Biomedical Imaging, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, 2Shenzhen College of Advanced Technology, University of Chinese Academy of Sciences, Shenzhen, China, 3Research Center for Medical AI, Shenzhen Institute of Advanced Technology,Chinese Academy of Sciences, Shenzhen, China
Synopsis
In this work, a novel biplanar matrix Z2 nonlinear gradient coil with an open structure has been designed, which could be employed in open spatial low-field MRI system, and an efficient encoding strategy for O-Space imaging was proposed in combination with the proposed biplanar matrix nonlinear gradient coil, which has the potential to shift the center placements (CP’s) in nonlinear gradient imaging without an external linear gradient field. The biplanar Z2 encoding field generated by a nonlinear gradient element consisting of curve segments was optimized and implemented to show the feasibility of this proposed biplanar matrix coil and encoding approach.
Introduction
Nonlinear gradient imaging, such as PatLoc imaging 1, O-Space imaging 2, Null Space imaging 3, 4D-RIO 4, FRONSAC imaging 5 etc., is an effective solution to solve the problem of excessive coupling caused by too many receiver coils employed in parallel imaging. Currently, most of the nonlinear gradient imaging systems mainly have focused on high-field research compared to the low-field MRI systems with open structures, and the insertion coil of the cylindrical or monoplanar structures was mainly applied to generate the non-linear gradient encoding magnetic field 6-9. And the process of nonlinear gradient encoding was executed in the existing linear gradient imaging systems through the combination of the linear gradient magnetic fields and the nonlinear gradient magnetic fields 10-12. Here, a type of biplanar matrix nonlinear gradient coil was proposed into an low-field MRI system with open space structures. The proposed biplanar matrix coil could execute the movement of the CP’s of Z2 nonlinear gradient field by controlling the running sequence of its different channels, unlike the conventional linear gradient field moving the different CP’s of the Z2 spherical harmonic 2,7. The simulation and preliminary experiments have showed the feasibility of this proposed biplanar matrix coil.Methods
The 3D model system of open low-field magnetic resonance with the proposed biplanar nonlinear gradient matrix coil has been designed and illustrated in Fig. 1. The biplanar non-linear gradient matrix coil is designed based on the target field method of current finite distribution, which can make the practical electrical current distribution closer to the actual systems, compared to the original unlimited current distribution 9,13,14. The original target magnetic field is defined and synthesized according to the application of the constant readout gradient with the field contour of $$$Z^{2}-\frac{1}{2}\left ( x^{2} +y^{2}\right )$$$, as seen as Fig. 2(a). The size per element of the proposed biplanar matrix coil which can generate a Z2 nonlinear gradient filed is 0.05 m × 0.05 m. The tiny current element should be defined on the surface where the final current distribution needs to be generated according to the Biot-Savart Law, as seen as Fig. 2(c). The double panel is placed at a distance of 50 cm due to the design requirement of the target field. The current weight matrix of the individual coil element can commonly be derived into, $$Ax=b$$, where A represents the magnetic field generated by the tiny current element with the unit current on the independent panel on all target points using the Biot-Savart Law; b represents the Z2 nonlinear gradient field. Here, the Tikhonov regularization is utilized to solve $$$x$$$ of the above inverse problem, when there are the large number of target fields and the large number of current elements. The final distribution of the current in the actual space is solved by using the stream function. The current contour maps are shown in Figs. 3(a) and 3(b), respectively. The actual distribution of the proposed coil after spatial quantization is shown in Fig. 3(c). A nonlinear gradient encoding strategy for O-Space imaging is proposed by controlling the coil energization at different time points, as seen as Fig. 4(a). Here, the proposed biplanar matrix Z2 nonlinear gradient coil of 4×4 element can move the CP position of the Z2 spherical harmonic field inside the FOV without combining the linear gradient magnetic field. Such as, the coil element can be energized in the joint sequence of t8 to t9, and t7 to t10 follow the direction of arrow, as seen as the black arrow in Fig. 4(b). The drive function of the linear gradient coil can be replaced by this encoding strategy, which can further reduce the hardware complexity and system cost for nonlinear gradient imaging. Otherwise, more elements of the proposed biplanar matrix Z2 nonlinear gradient coil can be extended for O-Space imaging.Results
The element of the proposed biplanar matrix nonlinear gradient coil based on the open structure was designed and built up with 1 mm diameter copper wire, as seen as Fig. 5(a). Here, the actual spatial distribution of the Z2 nonlinear gradient field was measured by transmitting 1A electric current into the prototype element of the proposed matrix coil. The actual measured magnetic field strength in the middle of the biplanar matrix coil well matched with the designed Z2 spherical harmonic field within the tolerance error, which can be seen in the blue and orange curves as Fig. 5(b). The coil element of this structure could be applied into Mosaic stitching a nonlinear gradient matrix coil to realize the Z2 nonlinear gradient encoding of different spatial positions in the FOV without mixing linear gradient magnetic fields, as seen as Fig. 4.Conclusions and Discussion
Nonlinear gradient imaging has great potential to compensate for the insufficient sensitivity of the receiving coil in accelerated parallel imaging 15-16. The Z2 harmonic field can be generated in the open structure system, using the proposed biplanar matrix nonlinear gradient coil. The practical working process of the biplanar matrix Z2 nonlinear gradient coil will be further developed and tested. And the in vivo imaging experiments will be done with the proposed biplanar matrix coil in clinical applications.Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (No.61871373 and No.81729003), the Natural Science Foundation of Guangdong Province (No.2018A0303130132) and the Pearl River Talent Recruitment Program of Guangdong Province (No.2019QN01Y986) and the Shenzhen Peacock Plan Team Program (No.KQTD20180413181834876).References
- Hennig J, Welz AM, Schultz G, et al. Parallel imaging in non-bijective, curvilinear magnetic field gradients: a concept study. MAGMA. 2008;21(1-2):5-14.
- Stockmann J P, Ciris P A, Galiana G, et al. O‐space imaging: highly efficient parallel imaging using second‐order nonlinear fields as encoding gradients with no phase encoding. Magnetic Resonance in Medicine. 2010;64(2):447-456.
- Tam L K, Stockmann J P, Galiana G, et al. Null space imaging: nonlinear magnetic encoding fields designed complementary to receiver coil sensitivities for improved acceleration in parallel imaging. Magnetic Resonance in Medicine. 2012;68(4):1166-1175.
- Gallichan D, Cocosco C A, Dewdney A, et al. Simultaneously driven linear and nonlinear spatial encoding fields in MRI. Magnetic Resonance in Medicine. 2011;65(3): 702-714.
- Wang H, Tam L K, Constable R T, et al. Fast rotary nonlinear spatial acquisition (FRONSAC) imaging. Magnetic Resonance in Medicine. 2016;75(3): 1154-1165.
- Stockmann J P, Galiana G, Tam L, et al. In vivo O‐Space imaging with a dedicated 12 cm Z2 insert coil on a human 3T scanner using phase map calibration. Magnetic Resonance in Medicine. 2013;69(2): 444-455.
- Jia F, Schultz G, Testud F, et al. Performance evaluation of matrix gradient coils. Magnetic Resonance Materials in Physics, Biology and Medicine. 2016;29(1): 59-73.
- Littin S, Gallichan D, Welz A M, et al. Monoplanar gradient system for imaging with nonlinear gradients. Magnetic Resonance Materials in Physics, Biology and Medicine. 2015;28(5): 447-457.
- Jia F, Littin S, Layton K J, et al. Design of a shielded coil element of a matrix gradient coil. Journal of Magnetic Resonance. 2017;281: 217-228.
- Wang H, Tam L, Kopanoglu E, et al. O-space with high resolution readouts outperforms radial imaging. Magnetic Resonance Imaging. 2017;37: 107-115.
- Wang H, Chang, Y, Liang D. Hybrid O-Space and FRONSAC Imaging. Proc. of the International Society for Magnetic Resonance in Medicine (ISMRM), Paris,France. 2018. Abstract Number: 4138.
- Wang H, Tam L, Kopanoglu E, et al. Experimental O‐space turbo spin echo imaging. Magnetic Resonance in Medicine. 2016;75(4): 1654-1661.
- Littin S, Jia F, Layton K J, et al. Development and implementation of an 84‐channel matrix gradient coil. Magnetic Resonance in Medicine. 2018;79(2): 1181-1191.
- Turner R. A target field approach to optimal coil design. Journal of Physics D: Applied physics. 1986;19(8): L147.
- Puy G, Marques J P, Gruetter R, et al. Spread spectrum magnetic resonance imaging. IEEE Transactions on Medical Imaging. 2011;31(3): 586-598.
- Dispenza N L, Littin S, Zaitsev M, et al. Clinical potential of a new approach to MRI acceleration. Scientific Reports. 2019;9(1): 1-10.
Figures
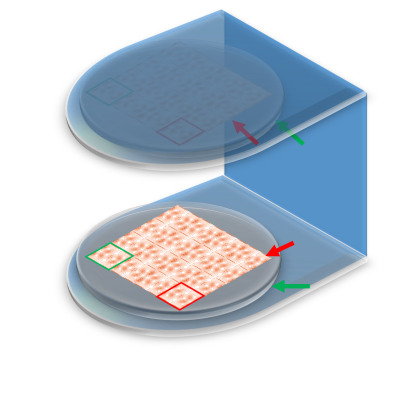
Fig. 1 The 3D model diagram of the proposed
biplanar matrix coil and the open-structure low-field MRI system. The green and
red boxes indicate the specific installation location of the coil. The
red and green arrows indicate the biplanar matrix coil and the low-field MRI
system, respectively.
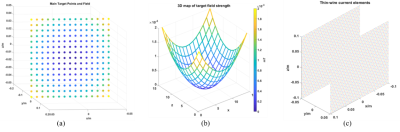
Fig. 2 Calculation of the target Z2
nonlinear gradient magnetic field. (a) represents the custom discrete target
field point with the size of 15 × 15 according to the application of a constant
read-out gradient with the shape of Z2 field. The magnetic field strength of each point is
demonstrated in (b). (c) shows that the tiny wire elements of the size of 51 ×
51 are used to calculate the magnetic field generated at the target point by
the Biot-Savart Law.
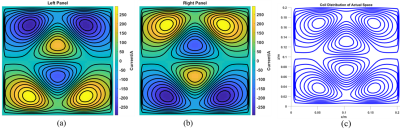
Fig. 3 Element contour of the target biplanar
matrix coil. (a), (b) represent the current contour map of the biplanar nonlinear
gradient coil to be solved through the flow function, respectively. (c)
represents the actual coil distribution in space obtained by quantizing the
current contour.
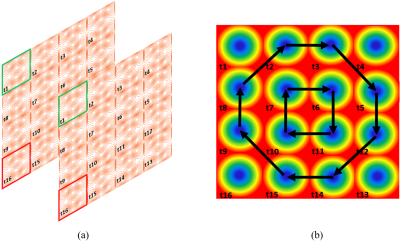
Fig. 4 Contour and
field of the proposed biplanar Matrix Z2 Nonlinear Gradient Coil (a) Matrix
coil composed of coil elements with the same structure. The green and red boxes
indicate the position of the coil, as seen as Fig. 1. (b) The model
diagram of the different CP’s positions of the Z2 spherical harmonic field
being moved at different times in (a). The energization sequence of the biplanar
matrix coil of 4×4 element is from t8
to t9, and t7 to t10 follow the arrow
direction.
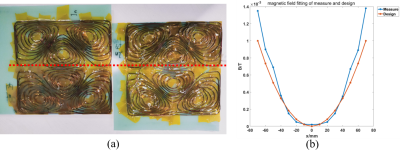
Fig. 5 The prototype element of the
proposed biplanar matrix coil. (a) The actual prototype element coil is built according
to the coordinate position of the element coil as seen as Fig. 2(c). (b) The
measured and designed magnetic field strengths are well matched at the middle
baseline of the coil as seen as the red line in (a).